Якщо варіанти вибірки є рівновіддаленими з кроком h, то вибіркове середнє й дисперсію можна знаходити за формулами:

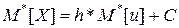
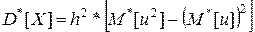
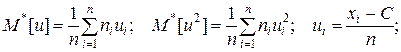
де С – умовний нуль, або варіанта, що має найбільшу частоту;

u_i - умовні варіанти,

Доцільно користуватися розрахунковою таблицею, що складається так:

1) у перший стовпчик таблиці записують вибіркові (початкові) варіанти, розташовуючи їх у зростаючому порядку;

2) у другий стовпчик записують частоти варіант; складають усі частоти і їхню суму (обсяг вибірки п) поміщають у нижню клітину стовпчика;

3) у третій стовпчик записують умовні варіанти 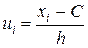, причому вважають h рівним різниці між будь-якими двома сусідніми варіантами;

4) перемножують частоти на умовні варіанти і записують їхні добутки 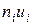 в четвертий стовпчик; суму  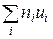поміщають у нижню клітину стовпчика;

5) перемножують частоти на квадрати умовних варіант і записують їхні добутки 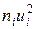 в п'ятий стовпчик; склавши отримані числа, їхню суму  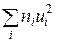поміщають у нижню клітину стовпчика;

6) перемножують частоти на квадрати умовних варіант, збільшених кожна на одиницю, і записують добутки 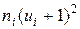 в шостий, контрольний стовпчик; склавши всі отримані числа, їхню суму  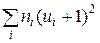поміщають у нижню клітину стовпчика.

Після того, як розрахункова таблиця заповнена, перевіряють обчислення за формулою

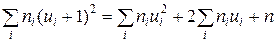
Обчислюють вибіркове середнє і дисперсію.

ПЕРЕВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ

Основні поняття

Статистичною гіпотезою називається будь-яке припущення щодо виду або параметрів невідомого розподілу.

Розрізняють прості й складні статистичні гіпотези. Простою називають гіпотезу, яка містить тільки одне припущення. Наприклад, якщо l - параметр показникового розподілу, то гіпотеза 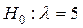 – проста.

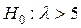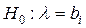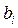Складною називають гіпотезу, що складається з скінченого або нескінченного числа простих гіпотез. Наприклад, гіпотеза  складна та складається з незліченної множини простих гіпотез , де  - будь-яке число більше 5.

Гіпотезу, що перевіряють, називають нульовою (або основною) і позначають 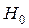. Альтернативною ( або конкуруючою) називають гіпотезу 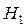, що є логічним запереченням  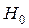і яку ми приймаємо, якщо відкидаємо основну гіпотезу.

Приклад. Нехай Н₀ полягає в тому, що математичне сподівання генеральної сукупності а = 3. Тоді ймовірні варіанти Н₁: а) а≠3; б) а>3; в) а<3.

При перевірці гіпотез можуть виникнути помилки двох видів. Помилка першого роду полягає в тому, що буде відкинута гіпотеза 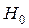, коли вона вірна.

Ймовірність помилки першого роду позначають a і називають рівнем значущості критерію.

Помилка другого роду полягає в тому, що буде прийнята гіпотеза 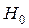, коли вона невірна. Ймовірність цієї помилки позначають b .

Ймовірність 1-b  не припуститися помилки другого роду, тобто відкинути гіпотезу 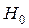, коли вона невірна, називається потужністю критерію. Чим більше потужність критерію, тим менше ймовірність помилки другого роду.

Яка з помилок є на практиці більш небезпечною, залежить від конкретної задачі. Наприклад, якщо перевіряється правильність вибору методу лікування хворого, то помилка першого роду означає відмовлення від правильної методики, що може сповільнити лікування, а помилка другого роду (застосування неправильної методики) чревата погіршенням стану хворого і є більш небезпечної.

Для перевірки нульової гіпотези використовують спеціально підібрану випадкову величину, яку називають статистичним критерієм.

Спостережуваним значенням критерію називається значення критерію, що обчислюється за вибіркою.

Після вибору статистичного критерію множину всіх його можливих значень розбивають на дві області, які не перетинаються. Це область відхилення нульової гіпотези та область прийняття цієї гіпотези. Критичною областю називається сукупність значень критерію, при яких нульову гіпотезу відкидають. Областю прийняття гіпотези називається сукупність значень критерію, при яких нульову гіпотезу приймають.

Основний принцип перевірки статистичних гіпотез: якщо спостере жуване значення критерію належить критичній області, гіпотезу відкидають; якщо спостережуване значення належить області прийняття гіпотези - гіпотезу приймають.

Отже, процес перевірки гіпотези складається з наступних етапів:

1. Вибирається статистичний критерій ДО.

2. Обчислюється його значення, що спостерігається, К_набл по наявній вибірці.

3. Оскільки закон розподілу ДО відомий, визначається (за відомим рівнем значимості α) критичне значення k_кр, що розділяє критичну область й область прийняття гіпотези (наприклад, якщо р(ДО > k_кр) = α, то праворуч від k_кр розташовується критична область, а ліворуч – область прийняття гіпотези).

4. Якщо обчислене значення К_спост попадає в область прийняття гіпотези, то нульова гіпотеза приймається, якщо в критичну область – нульова гіпотеза відкидається.

Розрізняють різні види критичних областей:

· правобічну критичну область, обумовлену нерівністю K > k_кр ( k_кр > 0);

· лівосторонню критичну область, обумовлену нерівністю K < k_кр ( k_кр < 0);

· двосторонню критичну область, обумовлену нерівностями K < k₁, K > k₂ (k₂ > k₁).

Потужністю критерію називають імовірність потрапляння критерію в критичну область за умови, що вірна конкуруюча гіпотеза. Після вибору рівня значимості варто будувати критичну область так, щоб потужність критерію була максимальною.