Нехай проведено п незалежних іспитів (п – досить велике число), у кожному з яких деяка подія А з'являється з однією і тією ж, але невідомою імовірністю р, і знайдена відносна частота 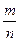 появ А в цієї серії іспитів. Перевіримо при заданому рівні значимості  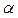нульову гіпотезу Н₀, що полягає в тому, що імовірність р дорівнює деякому значенню р₀.

Приймемо за статистичний критерій випадкову величину

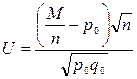 ,                               (2.1)

що має нормальний розподіл з параметрами M(U) = 0, σ(U) = 1 (тобто нормовану). Тут q₀=1–p₀. Висновок про нормальний розподіл критерію випливає з теореми Лапласа (при досить великому п відносну частоту можна приблизно вважати нормально розподіленою з математичним сподіванням р і середнім квадратичним відхиленням ).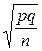

Критична область будується в залежності від виду конкуруючої гіпотези.

Якщо Н₀: р = р₀, а Н₁: р ≠ р₀, то критичну область потрібно побудувати так, щоб імовірність улучення критерію в цю область дорівнювала заданому рівню значимості α. При цьому найбільша потужність критерію досягається тоді, коли критична область складається з двох інтервалів, імовірність влучення в кожний з який дорівнює 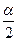. Оскільки U симетрична щодо осі Оу, імовірність її влучення в інтервали (–∞; 0) і (0; +∞) дорівнює 0,5, отже, критична область теж повинна бути симетрична відносно Оу. Тому і_кр визначається по таблиці значень функції Лапласа з умови 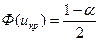, а критична область має вид . 

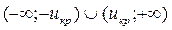Передбачається, що використовується таблиця значень функції Лапласа, заданої у вигляді 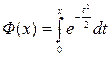, де нижня межа інтегрування дорівнює 0, а не -∞. Функція Лапласа, задана таким чином, є непарної, а її значення на 0,5 менше, ніж значення стандартної функції Ф(х).

Далі потрібно обчислити значення критерію, що спостерігається:

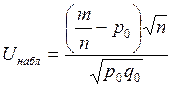.                                   (2.2)

Якщо |U_спост| < u_кр, то нульова гіпотеза приймається.

Якщо |U_спост| > u_кр, то нульова гіпотеза відкидається.

Якщо конкуруюча гіпотеза Н₁: р > p₀, то критична область визначається нерівністю U > u_кр, тобто є правобічною, причому р(U > u_кр)=α. Тоді 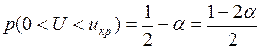. Отже, і_кр можна знайти за таблицею значень функції Лапласа за умови, що 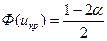. Обчислимо значення критерію, що спостерігається, за формулою (2.2).

Якщо U_спост < u_кр, то нульова гіпотеза приймається.

Якщо U_спост > u_кр, то нульова гіпотеза відкидається.

Для конкуруючої гіпотези Н₁: р < p₀ критична область є лівосторонньої і задається нерівністю U <- u_кр, де ікр обчислюється так само, як у попередньому випадку.

Якщо U_спост > - u_кр, то нульова гіпотеза приймається.

Якщо U_спост < - u_кр, то нульова гіпотеза відкидається.

ПРИКЛАД 7. Нехай проведено 50 незалежних іспитів, і відносна частота появи події А виявилася рівної 0,12. Перевіримо при рівні значимості α = 0,01 нульову гіпотезу Н₀: р = 0,1 при конкуруючій гіпотезі Н₁: р > 0,1. Знайдемо 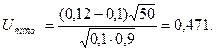 Критична область є правобічної, а і_кр знаходимо з рівності Ф(і_кр) = 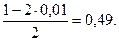З таблиці значень функції Лапласа визначаємо і_кр = 2,33. Отже, U_спост< u_кр, і гіпотеза про те, що р = 0,1, приймається.