Основними числовими характеристиками випадкової величини є математичне сподівання і дисперсія. Математичне сподівання характеризує середнє значення, біля якого групуються можливі випадкової величини, а дисперсія характеризує ступінь розкиданості цих значень щодо середнього.
Найбільш вживаними в статистичних дослідженнях є три види середніх: середня арифметична, мода і медіана. Вибір типу середньої для характеристики варіаційного ряду залежить від мети, для якої обчислюється середня, від особливостей вихідного матеріалу і від можливостей тієї чи іншої середньої.
Перш ніж перейти до характеристики окремих видів середньої, сформулюємо деякі, самі загальні вимоги до середнього.
Середня, являє собою кількісну характеристику якісно однорідної сукупності. Порушення цієї вимоги приводить до невірних висновків, спотворює суть явища.
Крім того, необхідно, щоб середня не була занадто абстрактної, а мала ясний сенс у вирішенні задачі.
Далі, бажано, щоб процедура обчислення середньої була проста. За інших рівних умов перевага віддається тієї середній, котра простіше обчислюється.
І, нарешті, при виборі середньої бажано звести до мінімуму вплив випадкових коливань вибірки. Так, якщо із однієї і тієї ж сукупності взяти кілька груп елементів, то середні, їм відповідні, будуть, як правило, розрізнятися за величиною. Рекомендується використовувати вид середньої, у якої ці розходження мінімальні.
Найбільш розповсюдженою мірою рівня – середня арифметична, що є аналогом математичного сподівання й обчислюється за формулою:
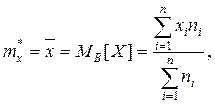
де xi – значення випадкової величини, що спостерігається в і-му досліді, п -число дослідів,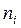 
.– частота і-ой варіанти.
Середня арифметична інтервального варіаційного ряду обчислюється в такий спосіб: за значення ознаки приймається середина інтервалу (центральне значення), що розраховується як арифметична середня границь інтервалу. Часто обчислення середньої арифметичної для інтервального варіаційного ряду ускладнюється тим, що невідомо або нижню границю першого інтервалу, або верхню границя останнього інтервалу, або ту й іншу одночасно. У таких випадках зазвичай (утім, у таких випадках часто відмовляються від обчислення середньої арифметичний, заміняючи її модою чи медіаною) умовно припускають, що інтервальна різниця невизначеного інтервалу така ж, що й у сусіднього. На основі цього припущення встановлюють границі крайніх інтервалів.
Крім середньої арифметичний широке поширення має інший вид мір рівня – медіана.
Медіаною (позначимо Mе) називається таке значення варіаційної ознаки, що приходиться на середину варіаційного ряду.
При обчисленні медіани дискретного варіаційного ряду можуть виникнути два випадки: 1) число варіант непарне (k=2m+1), 2) число варіант парне (k=2m). У першому випадку Me=xm+1, тобто медіана дорівнює центральної (серединної) варіанті ряду, у другому випадку Me=(xm+xm+1)/2, тобто медіана приймається рівній напівсумі, що знаходиться в середині ряду варіант.
ПРИКЛАД 3 . Нехай заданий ряд з непарним числом варіант:
| 
| 
| 
| 
| 
| 
| 
| 
|
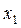
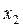
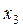
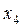
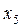
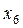
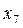
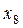
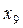
| 8 | 9 | 11 | 12 | 15 | 16 | 18 | 19 | 19 |
Тоді число варіант, дорівнює 9, представимо у вигляді 2m+1=9, звідти 2m=8, m=4, таким чином Me=x4+1=x5=15.
Розглянемо приклад парного числа варіант:
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
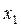
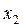
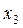
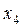
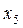
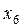
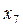
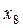
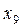
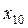
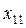
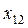
| 8 | 9 | 11 | 12 | 15 | 16 | 18 | 19 | 19 | 23 | 24 | 40 |
Тут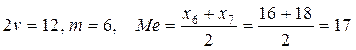 
.
Для інтервального варіаційного ряду медіана обчислюється за формулою
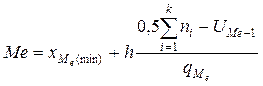
де xMe(min) – нижня границя медіанного інтервалу; h - величина цього інтервалу, чи інтервальна різниця; ni – частоти або частості;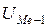 
– накопичена зверху частота (чи частість) інтервалу, що передує медіанному; qMe – частота чи частість медіанного інтервалу.
Зміст уведених позначень і процедуру обчислень розглянемо на конкретному прикладі.
ПРИКЛАД 4 . Обчислимо медіану за даними табл. 3.
Таблиця 3.
Розподіл господарств російських переселенців Чимкентского повіту за розміром посіву (1908р.)
| Розмір посіву xi, дес. | Усього господарств qi, % | Накопичені частоти
| Щільність розподілу |
| 0-4 4-8 8-12 12-16 16-20 Понад 20 | 16,6 24,4 19,1 23,9 9,7 6,3 | 16,6 41,0 60,1 84,0 93,7 100,0 | 4,15 6,10 4,78 2,99 0,97 |
Обчислення медіани починається з перебування інтервалу, що містить медіану. Медіанному інтервалу відповідає перша з накопичених частот чи частостей, що перевищує половину всього обсягу сукупності. У нашому випадку обсяг сукупності дорівнює 100%, перша з накопичених частостей, що перевищує половину всього обсягу сукупності – 60,1 (див. табл. 3). Отже, інтервал 8-12 буде медіанним. Далі, xme(min)=8, h=4,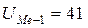 
, nMe=19,1. Маємо:
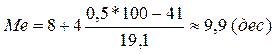
Таким чином, серединний розмір посіву дорівнює приблизно 9,9 дес.
Медіану можна використовувати в тих випадках, коли досліджувана сукупність неоднорідна, і в такій ситуації вона буде мати цілком конкретний зміст. Так, у розглянутому прикладі значення медіани має наступну інтерпретацію: в однієї половині господарств розмір посіву менше, в іншій – більше ніж 9,9 дес.
Особливо важливе значення медіана набуває при аналізі асиметричних рядів, тобто рядів, у яких навантажені (мають великі частоти) крайні чи близькі до крайнього значення варіант. Наприклад, медіана дасть більш вірне представлення про середній рівень особистих доходів групи родин у деякій країні, ніж середня арифметична, тому що медіана не настільки чуттєва до крайнього (нетиповим у плані постановки задачі) значенням (родини з великим доходом), як середня арифметична.
Медіану варто застосовувати, якщо обчислення середньої арифметичний неправомірне внаслідок невизначеності інтервалів (першого чи останнього, або того й іншого разом).
До достоїнств медіани варто віднести також те, що вона менш піддана випадковості вибірки, ніж середня арифметична.
Медіану не слід використовувати, коли число спостережень замале.
Поряд із середньою арифметичною і медіаною важливе значення як міра рівня має мода.
Модою (позначимо Мо) називається варіанта, що найбільш часто зустрічається в даному варіаційному ряді. Для дискретного ряду мода дорівнює варіанті з найбільшою частотою чи частістю. Для інтервального варіаційного ряду модальний інтервал, тобто інтервал що містить моду, визначається за найбільшою частотою (частістю) у випадку рівних інтервалів і за найбільшою щільністю у випадку нерівних інтервалів. Значення варіанти, дорівнює моді, відшукується за допомогою формули
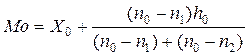
де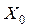 
- мінімальне значення модального інтервалу, 
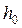- величина модального інтервалу, 
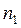– частота інтервалу, що передує модальному, 
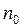– частота модального інтервалу, 
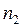– частота інтервалу, що слідує за модальним.
Досить грубе наближення можна одержати, узявши за моду центральне значення модального інтервалу, тобто середнє арифметичне границь інтервалу.
ПРИКЛАД 5 . Обчислимо моду за даними таблиці 3 попереднього прикладу. В останньому стовпці цієї таблиці обчислені щільності розподілу.
Найбільша щільність відповідає інтервалу 4-8. Це і є модальний інтервал.
Розраховуємо моду:
.
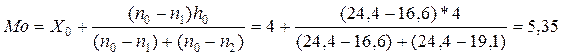Таким чином, одержуємо, що найбільш типовим за розміром посіву господарством російських переселенців Чимкентского повіту в 1908 р. було господарство, що засівало 5,35 десятин землі.
Мода має ті ж достоїнства, що і медіана. Мода і медіана ефективно використовуються як міри рівня, але порівняно із середньою арифметичною рідше вживаються як вихідний матеріал для більш складних методів математичної статистики.
Міри розсіювання. Розглянуті вище середні показують рівень варіаційного ряду, іншими словами, дозволяють ряд чисел охарактеризувати одним числом. Однак середні не містять у собі інформації про те, наскільки добре вони представляють усю сукупність. Однакові чи близькі за величиною середні можуть відноситися до дуже різних рядів.
Розмах варіації показує різницю між найбільшим і найменшим значеннями ознаки (R=xmax-xmin). Достоїнством цього показника є простота розрахунку. Однак можливості його застосування обмежені, тому що ця характеристика є найбільш грубою з усіх мір розсіювання.
По-перше, при розрахунку цього показника розсіювання ознаки використовуються тільки крайні значення ознаки, інші ж до уваги не приймаються. По-друге, розмах варіації істотно залежить від випадкових коливань вибірки.
Більш важливими для характеристики розсіювання ознаки є показники, при розрахунку яких використовуються відхилення усіх варіант від деякої середньої (наприклад середньої арифметичної або медіани). До таких мір розсіювання, зокрема, відносяться дисперсія й середньоквадратичне відхилення. Останні міри розсіювання менше будь-якої іншої міри піддаються випадковим коливанням вибірки. Середнє квадратичне відхилення і дисперсія знайшли широке застосування майже у всіх розділах математичної статистики
Аналогією дисперсії випадкової величини Х статистична (вибіркова) дисперсія обчислюється за формулою
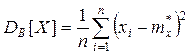
Вибіркова дисперсія є зміщеною оцінкою для дисперсії випадкової величини.
Незміщеною оцінкою дисперсії є виправлена вибіркова дисперсія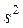 
, яка визначається із формулою:
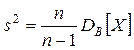
Аналогом середньоквадратичного відхилення є вибіркове середньоквадратичне відхилення
,
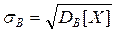величина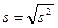 
є виправленим середньоквадратичним відхиленням.
При досить великих п (об'ємах вибірки)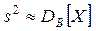 
.
Зауважимо, що, як і у випадку випадкової величини, справедлива така формула
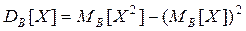
ПРИКЛАД 6. Розглянемо розподіл дореформеного наділу у селян Сімбірської губернії окремо для групи панщинних і групи оброчних селян (див. табл.4). Середні величини дореформених наділів для обох груп селян виявилися практично рівними (4,018 дес. у панщинних і 3,976 – в оброчних). З'ясуємо наскільки однаковою була варіація показників у цих групах. З цією метою обчислимо середньоквадратичне відхилення по сукупності панщинних і по сукупності оброчних селян.
Для обчислення середніх квадратичних відхилень зручно скласти допоміжну таблицю (табл. 5). У ній зафіксовані всі проміжні розрахунки.
З урахуванням цих результатів одержуємо середньоквадратичне відхилення для панщинних селян:
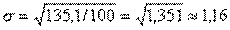
Таблиця 4.
Розміри дореформеного наділу в селян Сімбірської губернії.
|
| Наділ xi , дес. | ||||
| До 2 | С 2 до 3 | С 3 до 5 | С 5 до 7 | Свыше 7 | |
| Середини інтервалів Відсоток панщинних селян ni(1) Відсоток оброчних селян ni(2) | 1,0 1,8 12,4 | 2,5 18,4 17,5 | 4,0 63,5 48,2 | 6,0 15,2 13,3 | 8,0 1,1 8,6 |
і середньоквадратичне відхилення для оброчних селян:
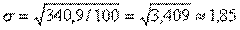
тобто, коливання ознаки в оброчних селян приблизно в півтора рази більше, ніж у панщинних.
Таким чином, середня величина дореформеного наділу в панщинних і оброчних селян Сімбірської губернії майже однакова, тобто в середньому ці групи селян за забезпеченістю землею практично не відрізняються. Але в середовищі оброчних селян розходження в розмірі наділів більше, ніж серед панщинних селян.
Таблиця 5.
Дані для обчислення середньоквадратичного відхилення.
| Розміри наделів дес. | Середини интервалів xi | Панщинні селяни | Оброчні селяни | ||||
| ni |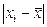 
| 
| 
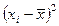
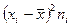
| ni |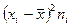 
| ||
| До 2 2-3 3-5 5-7 Понад 7 | 1,0 2,5 4,0 6,0 8,0 | 1,8 18,4 3,5 5,2 1,1 | 3,0 1,5 0 2,0 4,0 | 9,0 2,2 0 4,0 16,0 | 16,2 40,5 0 60,8 17,6 | 12,4 17,5 48,2 13,3 8,6 | 111,6 38,5 0 53,2 137,6 |
| Разом | 100,0 | 135,1 | 340,9 | ||||
Розглянуті вище міри розсіювання (розмах варіації, дисперсія, середньоквадратичне відхилення) є абсолютними величинами, судити по них про ступінь коливання ознаки не завжди можна, у деяких задачах необхідно використовувати відносні показники розсіювання. Таким показником є коефіцієнт варіації.
Коефіцієнт варіації (позначимо V) являє собою відношення середньоквадратичного відхилення до середньої арифметичної, вираженої у відсотках, тобто
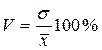
Коефіцієнт варіації дозволяє: 1) порівнювати варіацію ознаки в різних групах об'єктів, 2) виявити ступінь розходження ознаки в однієї і тієї ж групи об'єктів у різний час, 3) зіставити варіацію різних ознак у тих самих груп об'єктів.
Характеристиками форми розподілу є коефіцієнти асиметрії та ексцесу. Вибірковим коефіцієнтом асиметрії називається число
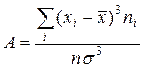
Якщо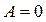 
, то розподіл має симетричну форму, тобто варіанти, рівновіддалені від 
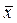, мають однакову частоту. При 
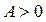розподіл має правосторонню асиметрію, при 
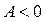лівосторонню.
Вибірковим коефіцієнтом ексцесу називається число
.
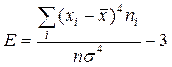Коефіцієнт ексцесу є показником «крутості» розподілу в порівнянні з нормальним.
Якщо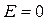 
, то розподіл с нормальним. Якщо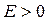 
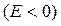, то полігон розподілу має більш круту (пологу) вершину в порівнянні з нормальною кривою.
Вибіркові коефіцієнти асиметрії та ексцесу використовуються для перевірки нормальності розподілу генеральної сукупності. Якщо А та Е близькі до нуля, то можна вважати, що вибірковий розподіл є нормальним.
Всі оцінки числових характеристик, розглянуті в даному розділі, є точковими, тому що вони визначаються одним числом. При вибірці малого обсягу точкова оцінка може значно відрізнятися від оцінюваного параметра, тобто приводити до грубих помилок. З цієї причини при невеликому обсязі вибірки варто користуватися інтервальними оцінками. Інтервальною називають оцінку, що визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють установити точність і надійність оцінок.
Надійністю (довірчою ймовірністю) оцінки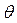 
по 
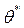називають імовірність 
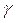, з якою здійснюється нерівність 
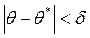. Звичайно надійність оцінки задається наперед, причому в якості 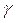беруть число, близьке до одиниці. Найбільше часто задають надійність, рівну 0,95; 0,99 й 0,999.
Нехай ймовірність того, що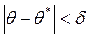 
, дорівнює :
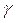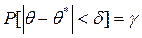
Замінивши нерівність рівносильною йому подвійною нерівністю маємо
.
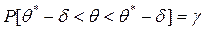Це співвідношення варто розуміти так: ймовірність того, що довірчий інтервал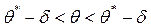 
“накриває” невідоме значення параметру 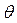, дорівнює 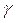. Величину 
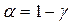називають рівнем значимості або ймовірністю помилки. Зауважимо, що кінці довірчого інтервалу є випадковими величинами.
Процедура побудови таких інтервалів називається інтервальним оцінюванням.
Довірчий інтервал для оцінки невідомого математичного сподівання нормального розподілу при відомому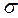 
можна знайти за допомогою співвідношення
,
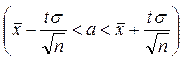де число t визначається з рівності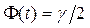 
за таблицею функції Лапласа (таблиця 2 Додатка). Значення цього твердження: довірчий інтервал покриває невідомий параметр а з надійністю 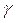; точність оцінки при цьому:
.
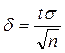Довірчий інтервал для оцінки математичного сподівання нормального розподілу при невідомому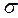 
можно знайти за допомогою співвідношення
,
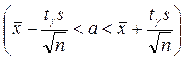где s – виправлене середньоквадратичне відхилення,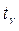 
– знаходится за таблицею 5 додатка.
Дата: 2019-02-02, просмотров: 573.
