Основные формулы:
Закон распределения молекул по скоростям – закон Максвелла – позволяет найти число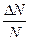 
, относительные скорости которых лежат в интервале от 
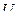до 
:
,
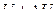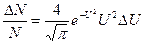где
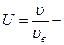относительная скорость,
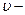данная скорость,
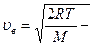наиболее вероятная скорость молекул,
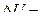величина интервала относительных скоростей, малая по сравнению со скоростью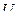
Барометрическая формула даёт закон убывания давления газа с высотой в поле силы тяжести:
,
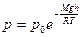где
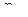давление газа на высоте 
,
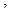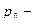давление газа на высоте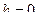 
Распределение частиц по значениям потенциальной энергии для внешнего потенциального поля – закон Больцмана:
,
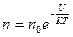где
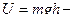потенциальная энергия,
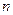и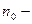 
концентрация молекул в точках, между которыми разность высот равна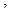
Примеры решения задач
1. Какая часть молекул кислорода при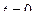 
˚ 
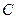обладает скоростями 
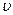от 
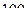до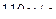 
?
Дано: Решение:
˚ 
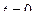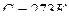Согласно закону Максвелла:
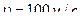
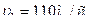
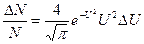
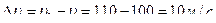
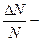? Наиболее вероятная скорость:
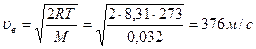
Относительная скорость:
; 
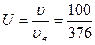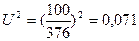
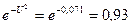
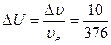
Таким образом, получаем:
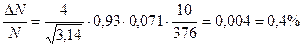
То есть число молекул, скорости которых лежат в заданном интервале, равно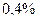 
заданного числа молекул.
Ответ: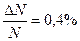 
2. Обсерватория расположена на высоте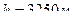 
над уровнем моря. Найти давление воздуха на этой высоте. Температуру воздуха считать постоянной и равной 
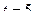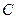˚ . Молярная масса воздуха 
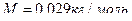. Давление воздуха на уровне моря 
.
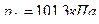Дано: Решение:
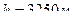Используя барометрическую формулу получим:
˚ 
?
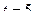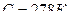
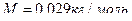
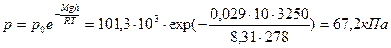
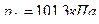
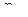Ответ: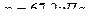 
3. Полагая температуру воздуха и ускорение свободного падения не зависящими от высоты, определить, на какой высоте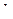 
над уровнем моря концентрация воздуха в 
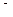раза меньше своего значения на уровне моря. Температуру воздуха считать равной 
˚ .
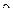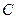Дано: Решение:
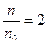Согласно закону Больцмана:
˚ 
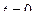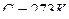
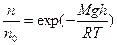
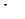? Таким образом:
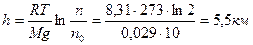
Ответ: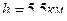 
Задачи для самостоятельного решения
1. При какой температуре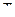 
средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на 
?
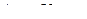(Ответ: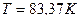 
)
2. Какая часть молекул азота при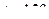 
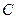˚ обладает скоростями 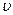от 
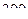до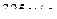 
?
(Ответ: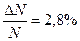 
)
3. Какая часть молекул водорода при 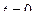˚ 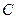обладает скоростями 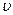от 
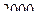до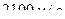 
?
(Ответ: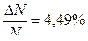 
)
4. Какая часть молекул азота при температуре 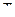имеет скорости, лежащие в интервале от 
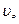до 
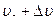, где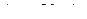 
, если
а)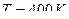 
;
б)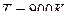 
При этом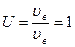 
(Ответ: а)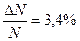 
;б)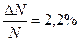 
)
5. На какой высоте давление воздуха составляет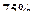 
от давления на уровне моря? Температуру воздуха считать постоянной и равной ˚ .
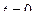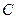(Ответ: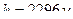 
)
6. Перрен, наблюдая при помощи микроскопа изменение концентрации взвешенных частиц гуммигута с изменением высоты и применяя барометрическую формулу, экспериментально нашёл значение постоянной Авогадро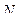 
. В одном из опытов Перрен нашёл, что при расстоянии между двумя слоями 
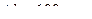число взвешенных частиц гуммигута в одном слое вдвое больше, чем в другом. Температура гуммигута 
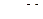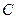˚ . Частицы гуммигута диаметром 
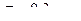были взвешены в жидкости, плотность которой на 
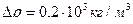меньше плотности частиц. Найти по этим данным значение постоянной Авогадро 
.
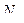(Ответ: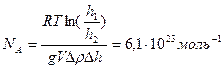 
)
7. Пассажирский самолёт совершает полёты на высоте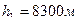 
. Чтобы не снабжать пассажиров кислородными масками, в кабине при помощи компрессора поддерживается постоянное давление, соответствующее высоте 
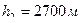. Найти разность давлений внутри и снаружи кабины. Температуру наружного воздуха считать равной 
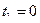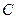˚ . Давление на уровне моря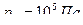 
(Ответ: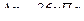 
)
Средняя энергия молекул
Основные формулы:
Средняя кинетическая энергия молекул:
,
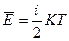где
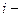число степеней свободы:
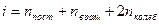
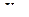постоянная Больцмана.
Внутренняя энергия идеального газа:
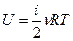
| Число степеней свободы(i) | Одноатомный газ | Двухатомный газ | Многоатомный газ |
Поступательных(  )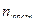
| 3 | 3 | 3 |
Вращательных(  )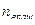
| - | 2 | 3 |
| Всего | 3 | 5 | 6 |
Скорости молекул:
-средняя квадратичная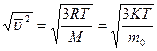 
- средняя арифметическая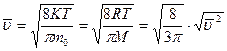 
,
где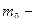 
масса молекулы
Средняя длина свободного пробега молекулы:
,
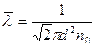где 
эффективный диаметр молекулы
Среднее число столкновений молекулы в единицу времени:
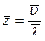
Примеры решения задач
1. Чему равна энергия теплового движение 
кислорода при температуре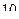 
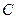˚ ? Какая часть этой энергии приходится на долю поступательного движения, какая часть на долю вращательного?
Дано: Решение:
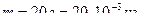Энергия теплового движения молекул газа:
˚ 
?
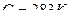
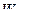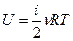
Кислород является двухатомным газом. Для двухатомного газ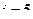 
, причём 
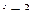приходится на долю поступательного движения молекул и 
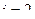- на долю вращательного движения.
Следовательно, получим:
; 
; 
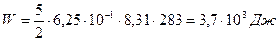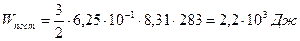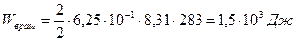
Ответ: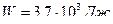 
; 
; 
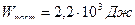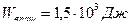
2. Какое число молекул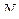 
двухатомного газа содержит объём 
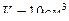при давлении 
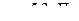и температуре 
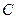˚ ? Какой энергией теплового движения 
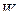обладают эти молекулы?
Дано: Решение:
Согласно уравнению Менделеева – Клапейрона:
˚ 
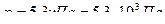
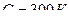
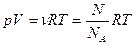
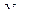? Но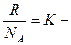 
постоянная Больцмана.
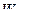? Отсюда окончательно имеем 
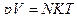, откуда
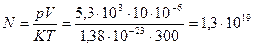
Энергия теплового движения двухатомного газа:
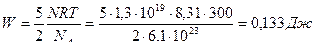
Ответ: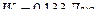 
3. При помощи ионизационного манометра, установленного на искусственном спутнике Земли, было обнаружено, что на высоте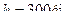 
от поверхности Земли концентрация частиц газа в атмосфере 
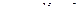. Найти среднюю длину свободного пробега 
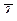частиц газа на этой высоте. Диаметр частиц газа 
.
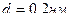Дано: Решение:
Средняя длина свободного пробега молекулы:
? 
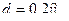
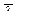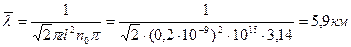
Ответ: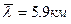 
4. Найти среднее число столкновений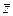 
в единицу времени молекул углекислого газа при температуре 
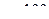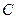˚ , если средняя длина свободного пробега 
.
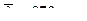Дано: Решение:
˚ 
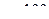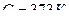Средняя длина свободного пробега молекулы:
? 
,
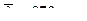
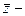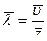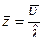, где
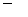средняя арифметическая скорость молекул:
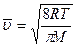
Следовательно:
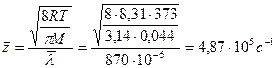, где
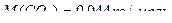
Ответ: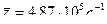 
Задачи для самостоятельного решения
1. Найти энергию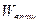 
вращательного движения молекул, содержащихся в массе 
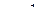азота при температуре 
˚ .
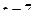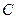(Ответ: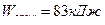 
)
2. Найти внутреннюю энергию 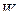двухатомного газа, находящегося в сосуде объёмом 
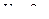под давлением 
.
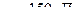(Ответ: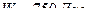 
)
3. Масса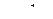 
двухатомного газа находится под давлением 
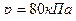, и имеет плотность 
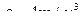. Найти энергию теплового движения 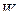молекул газа при этих условиях.
(Ответ: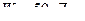 
)
4. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в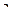 
водорода при температуре .
(Ответ: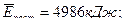 
)
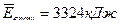5. Найти среднюю длина свободного пробега 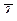молекул углекислого газа при температуре 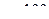˚ 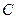и давлении 
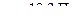. Диаметр молекул углекислого газа 
.
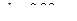(Ответ: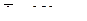 
)
6. Найти среднее число столкновений 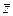молекул в единицу времени некоторого газа, если средняя длина свободного пробега 
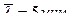, а средняя квадратичная скорость 
.
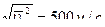(Ответ: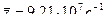 
)
7. Найти среднюю длина свободного пробега 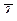молекул азота при давлении 
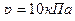и температуре ˚ .
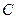(Ответ: 
)
Дата: 2018-12-28, просмотров: 305.
