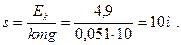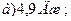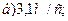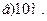Основные формулы
Закон сохранения импульса материальной точки
Если на материальную точку не действуют силы или они компенсируют друг друга, то ее импульс сохраняется
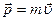 - импульс материальной точки.
- импульс материальной точки.
Согласно основному уравнению динамики материальной точки равнодействующая всех этих сил 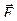 равна быстроте изменения импульса материальной точки:
равна быстроте изменения импульса материальной точки:
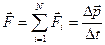 ,
,
где N – количество сил, действующих на материальную точку, i – номер силы, 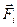 - величина i- ой силы,
- величина i- ой силы, 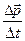 - скорость изменения импульса материальной точки.
- скорость изменения импульса материальной точки.
При 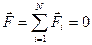 ,
, 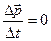 и
и 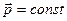 .
.
Закон сохранения импульса системы материальных точек
Если система содержит 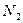 тел, на которые действуют
тел, на которые действуют 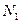 сил, то основное уравнение динамики применительно к такой системе примет вид:
сил, то основное уравнение динамики применительно к такой системе примет вид:
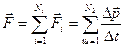 .
.
Основное уравнение динамики системы тел: сумма всех внешних сил, действующих на систему тел, равна скорости изменения суммарного импульса этой системы.
Система тел, на которую не действуют внешние силы, называется замкнутой
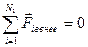 ,
, 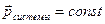 .
.
Закон сохранения момента импульса
Моментом импульса 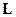 материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
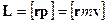 ,
,
где 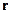 - радиус-вектор, проведенный из точки О в точку А.
- радиус-вектор, проведенный из точки О в точку А.
Модуль вектора момент импульса 
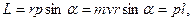
где 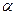 - угол между векторами
- угол между векторами 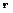 и
и 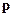 ,
, 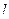 - плечо вектора
- плечо вектора 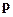 относительно точки О.
относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина 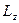 , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси
, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси
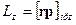 .
.
Закон изменения момента импульса со временем имеет вид:
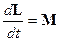 ,
,
где 
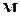 - момент сил
- момент сил
Производная момента импульса относительно оси равна моменту сил относительно той же оси
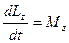 .
.
Момент импульса замкнутой системы сохраняется:
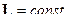
Закон сохранения энергии
В замкнутой системе тел, где между телами действуют только консервативные силы, полная механическая энергия системы сохраняется
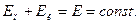
Примеры решения задач
1. Граната, летящая со скоростью 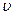 =10 м/с, разорвалась на два
=10 м/с, разорвалась на два
осколка. Больший осколок, масса которого составляла 0,6 массы всей гранаты, продолжал двигаться в том же направлении, но с увеличенной скоростью u =25 м/с. Найти скорость меньшего осколка.
 Дано: Дано:
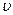 =10 м/с
m =10 м/с
m
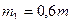 u =25 м/с
u =25 м/с

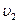 =? =?
| Решение:
Согласно закону сохранения импульса
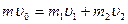 , ,
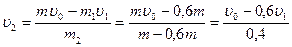 ; ;
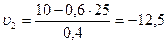 м/с.
Ответ: м/с.
Ответ: 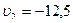 м/с. м/с.
|
2. Какую скорость 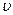 приобретает тележка (см. рисунок), если в нее соскользнет с ледяного холма камень? Трением можно пренебречь.
приобретает тележка (см. рисунок), если в нее соскользнет с ледяного холма камень? Трением можно пренебречь.
 Дано: Решение:
Дано: Решение:
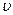 Согласно закону сохранения импульса:
Согласно закону сохранения импульса:
M 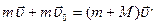 ,
,
m Направление скоростей совпадает, тогда: ,
H 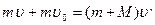 ,
, 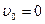 , следовательно,
, следовательно,

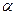
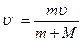
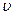 ’- ?
’- ?

Движение камня прямолинейное равномерное. Согласно второму закону Ньютона уравнение движения запишется в виде:
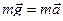 .
.
В проекции на ось ox уравнение движения имеет вид:
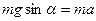 ,
,
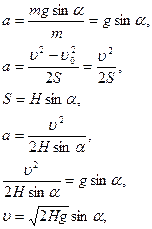
Следовательно,
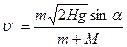 .
.
Ответ: 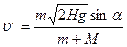 .
.
3. Два железнодорожных вагона массами 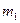 и
и 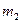 медленно дви-
медленно дви-
жутся в одну сторону со скоростями 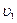 и
и 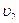 . Вагоны сталкиваются, и пружины буферов расталкивают их так, что удар можно считать упругим. Какова максимальная энергия W упругой деформации пружины?
. Вагоны сталкиваются, и пружины буферов расталкивают их так, что удар можно считать упругим. Какова максимальная энергия W упругой деформации пружины?
Дано:
 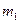
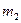
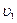
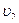
 W=?
W=?
| Решение:
В момент наибольшего сжатия пружины оба вагона имеют одинаковую скорость 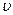 , которую можно найти из закона сохранения импульса: , которую можно найти из закона сохранения импульса:
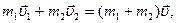 Направление движения вагонов совпадает с направление оси ox:
Направление движения вагонов совпадает с направление оси ox:
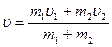
|
| Согласно закону сохранения энергии:
где W – максимальная энергия деформации пружины. Отcюда следует
Ответ: | |
4. Шайба А массы m, скользя по гладкой горизонтальной поверхности со скоростью v, испытала в точке О ( см. рис. ) упругое столкновение с гладкой неподвижной стенкой. Угол между направлением движения шайбы и нормалью к стенке равен 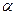 . Найти: а) точки , относительно которых момент импульса
. Найти: а) точки , относительно которых момент импульса 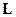 шайбы остается постоянным в этом процессе; в) модуль приращения момента импульса шайбы относительно точки О’, которая находится в плоскости движения шайбы на расстоянии от точки О.
шайбы остается постоянным в этом процессе; в) модуль приращения момента импульса шайбы относительно точки О’, которая находится в плоскости движения шайбы на расстоянии от точки О.
Решение:
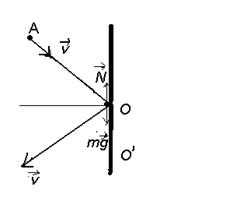
| Сила тяжести 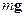 шайбы компенсируется силой реакции со стороны шайбы компенсируется силой реакции со стороны 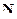 поверхности, по которой она скользит: поверхности, по которой она скользит:
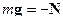 .
Момент силы, действующей на шайбу со стороны стены в момент удара будет равен нулю для всех точек на оси, перпендикулярной поверхности стены и проходящей через точку удара О, так как для этих точек радиус-вектор шайбы в момент удара и сила реакции со стороны стены параллельны друг другу. .
Момент силы, действующей на шайбу со стороны стены в момент удара будет равен нулю для всех точек на оси, перпендикулярной поверхности стены и проходящей через точку удара О, так как для этих точек радиус-вектор шайбы в момент удара и сила реакции со стороны стены параллельны друг другу.
|
Поэтому для всех этих точек 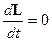 , то
, то  остается постоянным.
остается постоянным.
Момент импульса шайбы относительно точки О’ непосредственно перед ударом равен 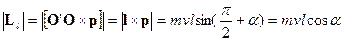
и направлен перпендикулярно плоскости скольжения шайбы вниз.
Сразу после момент импульса шайбы меняет направление на противоположное, не изменяясь по величине и, поэтому, модуль приращения момента импульса будет равен
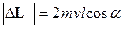 .
.
Ответ: а) Относительно всех точек на оси, перпендикулярной поверхности стены и проходящей через точку удара О;
б) 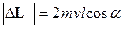
5. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) – одинакового радиуса 6 см и одинаковой массы 0,5 кг. Поверхности цилиндров окрашены одинаково. Как, наблюдая поступательные скорости цилиндров у основания наклонной плоскости, можно различить их? За какое время каждый цилиндр катится без скольжения с наклонной плоскости? Высота наклонной плоскости 0,5 м, угол наклона плоскости 300, начальная скорость каждого цилиндра равна нулю.
 Дано:
R 1 = R 2 = R =6 см
m =0,5 кг
h=0 , 5 м Дано:
R 1 = R 2 = R =6 см
m =0,5 кг
h=0 , 5 м
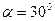
 t 1 =? t 2 =? t 1 =? t 2 =?
| Решение:
В отсутствие трения систему можно считать замкнутой. Каждой из тел в начальный момент обладает потенциальной энергией 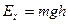 . Затем она преобразуется в кинетическую энергию поступательного движения . Затем она преобразуется в кинетическую энергию поступательного движения  и кинетическую энергию вращательного движения и кинетическую энергию вращательного движения 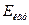 . .
|
| Таким образом, по закону сохранения полной механической энергии имеем
Тогда Что позволяет определить скорость
Так как скатывание цилиндров происходит под действием постоянной силы, то
Отсюда с учетом указанных выше формул имеем
Таким образом, чем больше мемент инерции тела, тем больше и вренмя скатывания. Так как для алюминиевого цилиндра
Аналогично для свинцового (полого) цилиндра
Ответ: 0,78 с; 0,88 с. | |
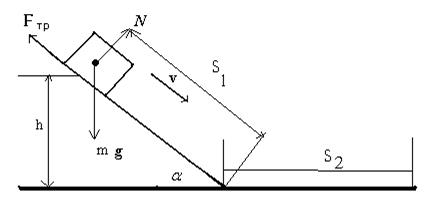
6. Тело массой 1 кг скользит сначала по наклонной плоскости высотой 1 м и длиной склона 10 м, а затем по горизонтальной поверхности. Коэффициент трения на всем пути равен 0,05. Найти: а) кинетическую энергию тела у основания плоскости; б) скорость тела у основания плоскости; в) расстояние, пройденное телом по горизонтальной поверхности до остановки.
 Дано:
m =1 кг
h =1 м
l =10 м
к=0,05 Дано:
m =1 кг
h =1 м
l =10 м
к=0,05
 Ек=?
v =?
S=?
Ек=?
v =?
S=?
| Решение:
|
| По закону изменения полной механической энергии где
В верхней точке у основания Следовательно, т.е. потенциальная энергия тела при соскальзывании с наклонной плоскости переходит в кинетическую энергию и в работу против сил трения.
а) б) в) Кинетическая энергия, которую имеет тело у основания наклонной плоскости, переходит в работу против сил трения на горизонтальной поверхности, т.е. Ответ:
| |
Задачи для самостоятельного решения
1. Тело массой m=1 кг, движущееся горизонтально со скоростью 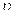 =1 м/с, догоняет второе тело массой M=0,5 кг и неупруго сталкиваются с ним. Какую скорость получат тела, если: а) второе тело стояло неподвижно; б) второе тело двигалось со скоростью u=0,5 м/с в том же направлении, что и первое тело; в) второе тело двигалось со скоростью u=0,5 м/с в направлении, противоположном направлению движения первого тела. (Ответ: а) u=0,67 м/с; б) u=0,83 м/с; в) u=0,5 м/с).
=1 м/с, догоняет второе тело массой M=0,5 кг и неупруго сталкиваются с ним. Какую скорость получат тела, если: а) второе тело стояло неподвижно; б) второе тело двигалось со скоростью u=0,5 м/с в том же направлении, что и первое тело; в) второе тело двигалось со скоростью u=0,5 м/с в направлении, противоположном направлению движения первого тела. (Ответ: а) u=0,67 м/с; б) u=0,83 м/с; в) u=0,5 м/с).
2. Пушка массой M=800 кг выстреливает ядро массой m=10 кг с начальной скоростью 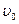 =200 м/с относительно Земли под углом
=200 м/с относительно Земли под углом 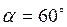 к горизонту. Какова скорость u отката пушки? Трением можно пренебречь. (Ответ:
к горизонту. Какова скорость u отката пушки? Трением можно пренебречь. (Ответ: 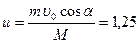 м/с).
м/с).
3. Шар массой m, движущийся со скоростью 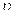 , налетел на покоящийся шар массой
, налетел на покоящийся шар массой 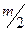 и после упругого удара изменил направление своего движения на угол
и после упругого удара изменил направление своего движения на угол 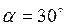 . С какими скоростями движутся шары после удара? (Ответ:
. С какими скоростями движутся шары после удара? (Ответ: 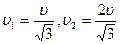 под углом 30
под углом 30  к начальной скорости первого).
к начальной скорости первого).
4. За счет чего увеличивается потенциальная энергия поднимающегося воздушного шара?
5. Груз массой 25 кг висит на шнуре длиной 2,5 м. На какую наибольшую высоту можно отвести в сторону груз, чтобы при дальнейших свободных колебаниях шнур не оборвался? Прочность шнура на разрыв 550 H. (Ответ: h=1,5 м).
6. Шарик массы m=1 кг бросили под углом 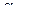 600 к горизонту с начальной скоростью
600 к горизонту с начальной скоростью 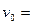 36 км/ч. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить L в вершине траектории. Сопротивлением воздуха можно пренебречь. (Ответ:
36 км/ч. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить L в вершине траектории. Сопротивлением воздуха можно пренебречь. (Ответ: 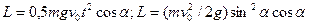 ).
).
7. Тело скользит сначала по наклонной плоскости, составаляющей угол 80 с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения на всем пути, если известно, что тело проходит по горизонтальной поверхности то же расстояние, что и по наклонной плоскости до остановки. (Ответ: 0,06).
8. Камень брошен со скоростью 15 м/с под углом 600 кинетическую, потенциальную и полную энергию камня: а) через 1 с после начала движения; б) в высшей точке траектории. (Ответ: 6,6 Дж; 15,9 Дж; 22,5 Дж б) 5,6 Дж; 16,9 Дж).
Дата: 2018-12-28, просмотров: 509.
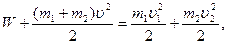
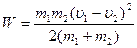 .
.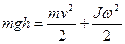 .
.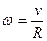 .
.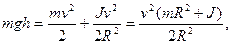
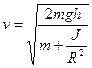 .
.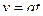 ,
,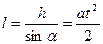
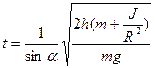 .
.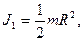 то
то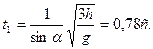
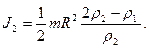 Тогда
Тогда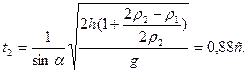
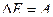 ,
,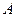 - работа внешних сил.
- работа внешних сил.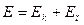 .
.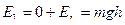 ,
,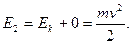
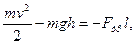
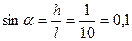 ;
; 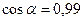 .
.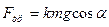 .
.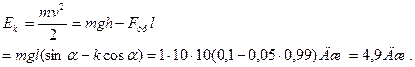
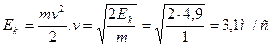
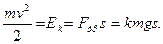 Отсюда
Отсюда