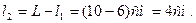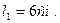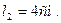Основные формулы
Основной закон динамики (II закон Ньютона): 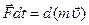 . Если m=const, то
. Если m=const, то 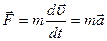 , где
, где 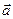 - ускорение, приобретаемое телом массой m под действием силы
- ускорение, приобретаемое телом массой m под действием силы 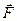 .
.
Равнодействующая всех сил равна 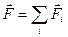 .
.
Сила трения 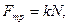 где
где 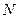 - сила нормального давления, k – коэффициент трения.
- сила нормального давления, k – коэффициент трения.
Сила тяжести: 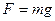 .
.
Вес тела:  , где m – масса тела, g – ускорение свободного падения.
, где m – масса тела, g – ускорение свободного падения.
Две материальные точки притягиваются друг к другу с силой Авиитации  , где
, где  - гравитационная постоянная, R – расстояние между их центрами.
- гравитационная постоянная, R – расстояние между их центрами.
Сила, вызывающая упругую деформацию х, пропорциональна величине деформации, т.е.
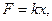
где к- коэффициент деформации.
Примеры решения задач
Динамика материальной точки и тела движущегося поступательно
3.1. С какой силой давит на дно лифта человек массой 60 кг, если а) ускорение лифта направлено вверх и б) ускорение лифта направлено вниз? В обоих случаях ускорение равно 1 м/с2.
 |
Дано:
m =60 кг
а=1м/с2
 P -?
P -?
| Решение: Движется человек вместе с лифтом относительно поверхности Земли. Масса человека задана, масса лифта – нет, следовательно, при решении можно брать во внимание только человека. Со стороны Земли на человека действует сила тяжести; со стороны опоры (пола лифта) на человека действует сила реакции опоры. Выберем одномерную систему отсчета с осью Oy, направленной вверх. |
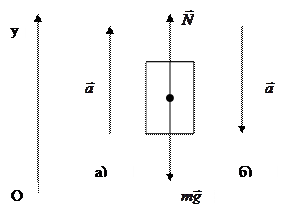
Уравнение в векторной форме: 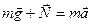 .
.
Согласно третьему закону Ньютона 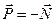 .
.
Найдем проекции векторов на ось Oy:
а). 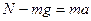 ;
;
Поскольку N = P, то  , следовательно:
, следовательно:
 .
.

б). 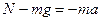 ,
,
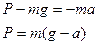 .
.
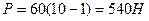
Ответ: a). P=660 H; б). P=540 H.
2. Тело соскальзывает с наклонной плоскости без начальной скорости. Угол наклона плоскости к горизонту 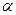 =30
=30 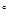 , длина наклонной плоскости l =2 м, коэффициент трения тела о плоскость
, длина наклонной плоскости l =2 м, коэффициент трения тела о плоскость 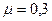 . С каким ускорением движется тело? Сколько времени длится соскальзывание?
. С каким ускорением движется тело? Сколько времени длится соскальзывание?
 Дано: Дано:
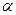 =30 =30 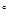 l =2 м
l =2 м
  a-?
t-?
a-?
t-?
| Решение: Обозначим все силы, действующие на тело. |
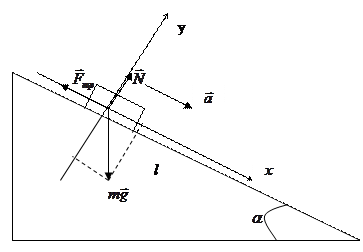
Согласно основному закону динамики можно записать уравнение движения тела: 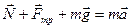 .
.
Выберем систему координат, запишем проекции векторов на оси Ox и Oy:
Ox: 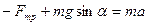 ; (1)
; (1)
Oy: 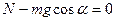 ;
;
 ;
;
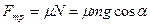 ;
;
Из уравнения (1) выразим ускорение a:
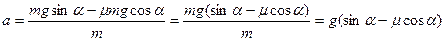 ;
;
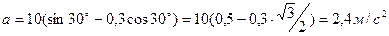 .
.
Тело движется прямолинейно и равноускоренно, следовательно,
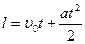 ; т.к.
; т.к.  =0 (согласно условию задачи «без начальной скорости»)
=0 (согласно условию задачи «без начальной скорости»)
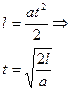 .
.
В общем виде выражение для времени запишется в виде:
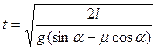 .
.
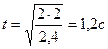 .
.
Ответ:  ;
; 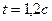 .
.
3. Тело массой m=0,5 кг движется прямолинейно, причем координата тела Х изменяется от времени как  , где с=5 м/с2 и d=1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
, где с=5 м/с2 и d=1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
 Дано: Решение:
Дано: Решение:
m=0,5 кг Отметим силы, действующие на т
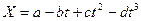
с=5 м/с2
 d=1 м/с3
d=1 м/с3
|
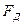 -?
-?
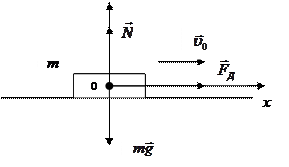
Согласно основному закону динамики (II закону Ньютона) 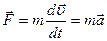 .
.
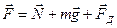 , где
, где  - действующие на тело силы. Выберем систему координат. Запишем проекции векторов на оси ox и oy:
- действующие на тело силы. Выберем систему координат. Запишем проекции векторов на оси ox и oy:
Ox : 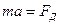 ;
;
Oy : 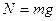
Ускорение находится как вторая производная от координаты по времени:
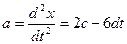 .
.
Найдем силу F, действующую на тело в конце первой секунды движения: 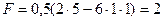 H.
H.
Ответ: F =2 H.
4. К концам шнура, перекинутого через блок, подвешены грузы с массами m 1 =100 г и m 2=150 г. Найдите ускорение грузов, силу натяжения шнура Т и показание F динамометра, на котором висит блок.
 Дано: Решение:
Дано: Решение:
m 1 =100 г=0,1 кг Обозначим все силы, которые действуют на систему:
m 2=150 г=0,1 кг
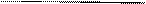
Т-?
F-?
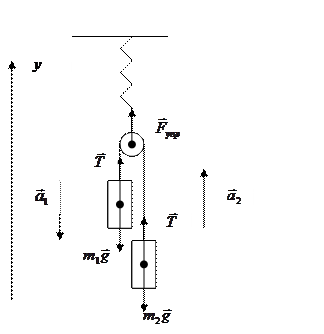
Благодаря нерастяжимости шнура перемещения обоих грузов одинаковы по величине; значит, одинаковы по величине и их ускорения: 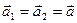 . Пренебрегая массами шнура и блока, а также трением в блоке, можно считать силу Т натяжения шнура всюду одинаковой. Запишем уравнения второго закона Ньютона для каждого из грузов:
. Пренебрегая массами шнура и блока, а также трением в блоке, можно считать силу Т натяжения шнура всюду одинаковой. Запишем уравнения второго закона Ньютона для каждого из грузов:
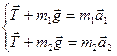 ;
;
Найдем проекции на ось y:
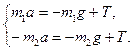 (1)
(1)
(2)
Вычтем из (1) уравнения (2), найдем ускорение:
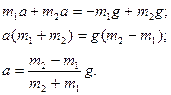
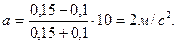
Найдем натяжение шнура, для этого к (1) уравнения прибавим (2):
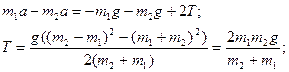
 .
.
Для нахождения силы упругости F упр пружины динамометра надо рассмотреть силы, действующие на блок:
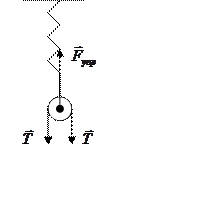
Из условия равновесия блока получаем, что F упр =2T=2,4 H.
Ответ: a =2 м/с2, T =1,2 H , F упр =2,4 H .
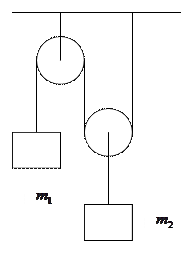
5. В показанной на рисунке системе 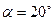 , m 1=2 кг, m 2=1 кг. Коэффициент трения между первым грузом и наклонной плоскостью
, m 1=2 кг, m 2=1 кг. Коэффициент трения между первым грузом и наклонной плоскостью 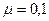 . Грузы опускают без начальной скорости. А). Найдите ускорение a системы грузов и силу натяжения нити T . Б). Как изменится ответ, если коэффициент трения станет равным 0,3?
. Грузы опускают без начальной скорости. А). Найдите ускорение a системы грузов и силу натяжения нити T . Б). Как изменится ответ, если коэффициент трения станет равным 0,3?
 Дано: Дано:
 m 1=2 кг
m 2 =1 кг
m 1=2 кг
m 2 =1 кг
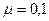
 а) a -?
T -?
Б) а) a -?
T -?
Б) 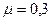 a -?
T -?
a -?
T -?
| Решение:
Рассмотрим движение каждого груза отдельно, указав предварительно все действующие на Аждый груз силы.
Второй закон Ньютона для первого груза, т.е. его динамическое уравнение имеет вид:
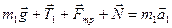 . .
|
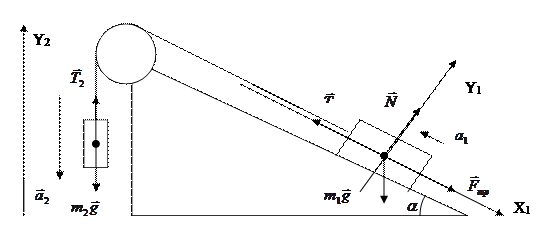
Проецируя это уравнение на выбранные оси ОХ1 и OY1, получаем:
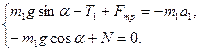
Из второго уравнения полученной системы находим, что
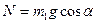 ,
,
поэтому
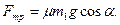 .
.
Подставим значение силы трения в первое уравнение системы, имеем
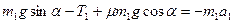 , (1)
, (1)
Запишем второй закон Ньютона для второго груза, проецируя его на ось OY2:
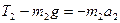 ,
,  (2)
(2)
Сложим уравнения (1) и (2), учитывая, что 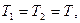
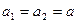 , получим:
, получим:
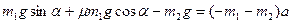 ,
,
Откуда:
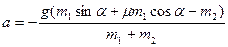 ,
,
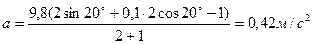 .
.
Из уравнения (2):
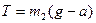 ,
,
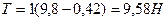 .
.
Б). 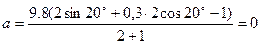 ,
,
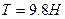 .
.
Ответ: а) а=0,42 м/с2, T =9,58 H , б) а=0 м/с2, T =9,8 H .
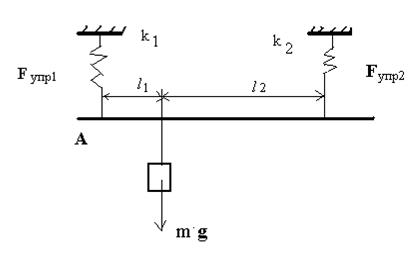
Задача 6. На двух параллельных пружинах одинаковой длины висит стержень, весом которого можно пренебречь. Коэффициенты деформации пружин равны соответственно 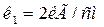 и
и 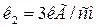 . Длина стержня равна расстоянию между пружинами L =10 см. В каком месте стержня надо подвесить груз, чтобы стержень оставался горизонтальным?
. Длина стержня равна расстоянию между пружинами L =10 см. В каком месте стержня надо подвесить груз, чтобы стержень оставался горизонтальным?
 Дано: Дано:
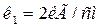
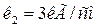 L =10 см
L =10 см
 l 1 =? L 2 =?
l 1 =? L 2 =?
| Решение:
|
| Чтобы система находилась в равновесии, т.е. чтобы стержень был в горизонтальном положении, необходимо выполнение двух условий:
В проекции на ось х уравнение (1) имеет вид:
Отсюда Моменты сил относительно точки А:
Тогда из уравнения (2) Учитывая решение (4), имеем
Так как Ответ: | |
|
| |
Динамика криволинейного движения материальной точки
Основные формулы
Второй закон Ньютона для вращательного движения материальной точки: 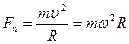 , где
, где 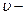 линейная скорость,
линейная скорость,  - угловая скорость, R – радиус кривизны траектории в данной точке.
- угловая скорость, R – радиус кривизны траектории в данной точке.
Примеры решения задач
7. Определить силу давления лыжника массой 70 кг на снег при равномерном движении со скоростью 20 м/с: а) на горизонтальном участке дороги; б) на середине вогнутого участка; в) на середине выпуклого участка. Радиус кривизны криволинейных участков 80 м. Силой трения пренебречь.
 Дано:
m= 70 кг Дано:
m= 70 кг
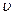 =20 м/с
R =80 м =20 м/с
R =80 м
 P-?
P-?
| Решение:
Во всех трех случаях на лыжника действуют две реальные силы:
сила тяжести и сила реакции опоры, которые направлены по вертикали в противоположные стороны. Динамическое уравнение движения в векторном виде:
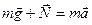 . .
|

Ось y направим вертикально вверх (рисунок а). Когда лыжник движется равномерно по горизонтальному участку, он не испытывает никаких ускорений в вертикальном направлении, тогда:
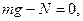
откуда

По третьему закону Ньютона лыжник действует на снег силой P , равной по величине N и противоположной ей по направлению, т.е.
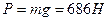 .
.
Двигаясь равномерно по вогнутому участку (рисунок б), лыжник испытывает центростремительное ускорение, направленное по радиусу к центру окружности. В этом случае уравнение движения примет вид:
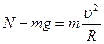 .
.
Отсюда, аналогично случаю а) найдем:
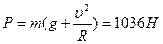 .
.
Двигаясь равномерно по выпуклому участку (рисунок в), лыжник, как и в случае б), испытывает центростремительное ускорение, направление по радиусу к центру окружности. Уравнение движения примет вид:
 .
.
Отсюда, аналогично предыдущим случаям, найдем:
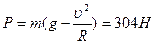 .
.
Ответ: а) 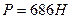 , б)
, б) 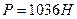 , в)
, в) 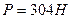 .
.
8. Шарик, подвешенный на нити длиной l, равномерно движется по окружности в горизонтальной плоскости. При этом нить все время образует с вертикалью угол 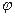 (такую систему называют коническим маятником). Найдите период T вращения шарика.
(такую систему называют коническим маятником). Найдите период T вращения шарика.
 Дано: Решение:
Дано: Решение:
l Обозначим все силы, которые действуют на тело

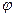 Согласно второму закону Ньютона:
Согласно второму закону Ньютона:
T =?  .
.
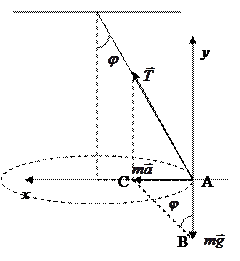
Спроецируем это уравнение на выбранные направления oy и ox :
ox : 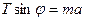 , (1)
, (1)
oy: 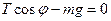 . (2)
. (2)
Из треугольника АВС следует, что  , следовательно,
, следовательно, 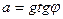 .
.
С другой стороны, 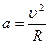 , где
, где 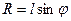 . Тогда
. Тогда  .
.
Разделим почленно уравнение (1) на (2):
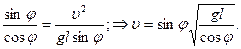
При равномерном движении шарика по окружности его период вращения определяется следующим образом:
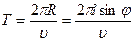 .
.
Подставим выражение для 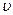 в уравнение для T , получим:
в уравнение для T , получим:
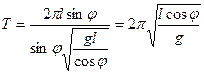 .
.
Ответ: 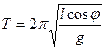 .
.
Задачи для самостоятельного решения
1. На однородный стержень длиной l действуют две растягивающие силы  и
и 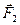 , приложенные к его концам. С какой силой F растянут стержень в сечении, находящемся на расстоянии x от точки приложения силы
, приложенные к его концам. С какой силой F растянут стержень в сечении, находящемся на расстоянии x от точки приложения силы  ? (Ответ:
? (Ответ: 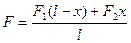 ).
).
2. На гладком столе лежат два связанных бруска массами 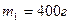 и
и 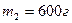 . К одному из них приложена горизонтальная сила F=2H/ Найдите силу T натяжения нити, если сила приложена: а). к первому бруску; б). ко второму бруску.
. К одному из них приложена горизонтальная сила F=2H/ Найдите силу T натяжения нити, если сила приложена: а). к первому бруску; б). ко второму бруску.

(Ответ: а) 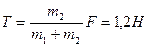 , б)
, б) 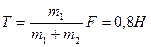 ).
).
3. Тело соскальзывает с наклонной плоскости без начальной скорости. Угол наклона плоскости к горизонту 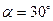 , длина наклонной плоскости l =2 м, коэффициент трения тела о плоскость
, длина наклонной плоскости l =2 м, коэффициент трения тела о плоскость 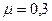 . С каким ускорением движется тело? Сколько времени длится соскальзывание? (Ответ:
. С каким ускорением движется тело? Сколько времени длится соскальзывание? (Ответ: 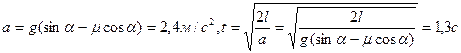 ).
).
4. Если наклонить доску под углом  к горизонту, кирпич будет двигаться по ней практически равномерно. За какое время t кирпич проедет всю доску, если наклонить ее под углом
к горизонту, кирпич будет двигаться по ней практически равномерно. За какое время t кирпич проедет всю доску, если наклонить ее под углом 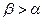 ? Длина доски равна l. (Ответ:
? Длина доски равна l. (Ответ: 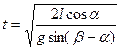 ).
).
5. Через блок, укрепленной на ребре призмы, перекинута нить с грузами на концах. Найдите ускорение грузов а и силу натяжения нити Т.Трением можно пренебречь. (Ответ: 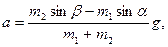
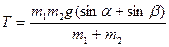 ).
).

6. На наклонной плоскости с коэффициентом трения k лежит тело массой М .Нарисовать график зависимости силы трения, действующей на тело, в зависимости от угла наклона  наклонной плоскости. (Ответ:
наклонной плоскости. (Ответ: 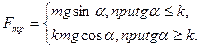 ).
).
7. Наклонная плоскость, образующая угол 25  с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения о плоскость. (Ответ:
с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения о плоскость. (Ответ: 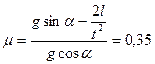 ).
).
8. При падении тела с большой высоты его скорость при установившемся движении достигает 80 м/с. Определить время, в течение которого , начиная с момента начала падения, скорость становится равной половине установленной. Силу сопротивления воздуха принять пропорциональной скорости тела. (Ответ:  ).
).
9. К концам однородного стержня приложены две противоположно направленные силы: 40Н и 100Н. Определить силу натяжения стержня в поперечном сечении, которое делит стержень на две части в отношении 1:2. (Ответ:  ).
).
10. Грузы m 1=1 кг и m 2=2 кг движутся вдоль вертикальной оси с помощью системы одинаковых блоков и невесомой и нерастяжимой нити. С каким ускорением движется первое тело? (Ответ: 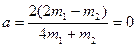 ).
).
11. Определить жесткость системы из двух пружин, если жесткость одной из них равна 2 кН/м, а другой – 6 кН/м: а) при их последовательном соединении, б) при их параллельном соединении (Ответ: 1,5 кН/м; 8 кН/м)
11. Шарик массой 200 г, подвешенный к потолку на нити длиной 1 м, описывает в горизонтальной плоскости окружность, имея при этом постоянную скорость. Определить скорость шарика и период его вращения по окружности, если нить составляет с вертикалью угол 60  . (Ответ:
. (Ответ: 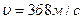 ,
,  ).
).
12. Космическая ракета летит на Луну. В какой точке прямой, соединяющей центры масс Луны и Земли, ракета будет притягиваться Землей и Луной с одинаковой силой? (Ответ: 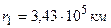 .)
.)
Дата: 2018-12-28, просмотров: 401.
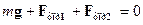 , (1)
, (1)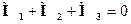 . (2)
. (2)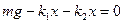 . (3)
. (3)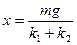 . (4)
. (4)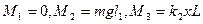 .
.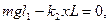
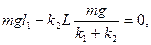
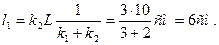 .
.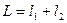 ,
,