Основные формулы
Постулаты Эйнштейна:
1-й постулат: любые физические процессы протекают одинаково во всех инерциальных системах отсчета;
2- ой постулат: скорость света в вакууме абсолютна, т.е. одинакова относительно любых инерциальных систем отсчета.
Если промежуток времени между двумя событиями в неподвижной относительно наблюдателя инерциальной системы отсчета равен 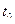 , то промежуток времени между этими же событиями в движущейся инерциальной системе отсчета:
, то промежуток времени между этими же событиями в движущейся инерциальной системе отсчета:
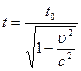 ,
,
где 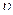 - скорость движущейся системы отсчета.
- скорость движущейся системы отсчета.
Если длина объекта в неподвижной относительно наблюдателя инерциальной системы отсчета равна 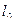 , то длина этого же объекта в движущейся со скоростью
, то длина этого же объекта в движущейся со скоростью 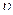 системе равна:
системе равна:
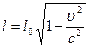 .
.
Если инерциальная система отсчета движется со скоростью 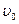 относительно неподвижной системы отсчета, а в ней частица движется в том же направлении со скоростью
относительно неподвижной системы отсчета, а в ней частица движется в том же направлении со скоростью 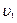 относительно движущейся системы, то скорость частицы
относительно движущейся системы, то скорость частицы 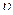 относительно неподвижной системы отсчета
относительно неподвижной системы отсчета
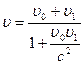 .
.
Собственная энергия 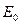 частицы связана с ее инвариантной массой
частицы связана с ее инвариантной массой 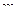 формулой
формулой
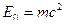 .
.
Релятивистская энергия 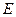 связана с импульсом массовой частицы
связана с импульсом массовой частицы 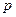 соотношением
соотношением
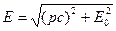 .
.
Импульс массовой частицы связан с ее скоростью  формулой
формулой
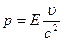 .
.
Импульс безмассовой частицы 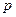 связан с ее энергией
связан с ее энергией 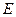 формулой
формулой
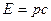 .
.
Энергия 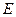 массовой частицы связана с ее скоростью
массовой частицы связана с ее скоростью  формулой
формулой
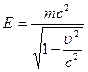 .
.
Кинетическая энергия 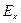 массовой частицы связана с ее скоростью формулой
массовой частицы связана с ее скоростью формулой

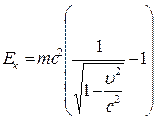 .
.
Полная энергия массовой частицы связана с ее собственно энергией 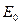 и кинетической энергией
и кинетической энергией 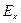 соотношением
соотношением
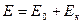 .
.
Релятивистская масса 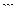 движущейся со скоростью
движущейся со скоростью  частицы связана с ее массой покоя
частицы связана с ее массой покоя 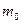 формулой
формулой
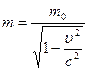 .
.
Примеры решения задач
1. При какой относительной скорости движения релятивистское сокращение длины движущегося тела составляет 25 %?
 Дано: Дано:
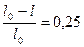 v=?
v=?
| Решение:
Имеем 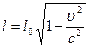 . (1)
По условию . (1)
По условию 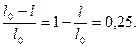 Отсюда Отсюда 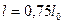 . (2)
Подставляя (2) в (1), получим . (2)
Подставляя (2) в (1), получим 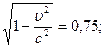 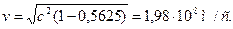 Ответ:
Ответ: 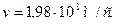
|
2. Во сколько раз увеличивается продолжительность существования нестабильной частицы по часам неподвижного наблюдателя. Если она начинает двигаться со скоростью, составляющей 99 % скорости света?
Дано:
 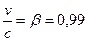
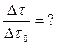
| Решение:
Промежуток времени 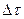 в сиcтеме, движущейся со скоростью v по отношению к наблюдателю, связан с промежутком времени в сиcтеме, движущейся со скоростью v по отношению к наблюдателю, связан с промежутком времени 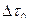 в неподвижной для наблюдателя системе соотношением в неподвижной для наблюдателя системе соотношением
|
|
Ответ: | |
3.Две частицы в некоторый момент времени находятся на расстоянии S =1 км друг от друга и движутся навстречу друг другу со скоростями 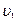 =0,4с и
=0,4с и 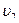 =0,6с. Через какое время
=0,6с. Через какое время 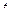 они столкнутся?
они столкнутся?
 Дано:
S =1 км =1000 м Дано:
S =1 км =1000 м
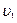 =0,4 с =0,4 с
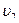 =0,6 с
с= =0,6 с
с= 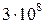 м/с м/с

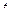 -? -?
| Решение:
Время сближения частиц 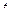 определим из уравнения равномерного движения определим из уравнения равномерного движения
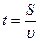 ,
где ,
где  - скорость, с которой одна из частиц приближается к другой. - скорость, с которой одна из частиц приближается к другой.
|
| Ее найдем по формуле:
Подставив в уравнение для времени, решим задачу в общем виде:
Имеем: Ответ:
| |
4.Чему равна скорость 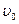 одной инерциальной системы отсчета относительно другой, если скорость частицы относительно одной системы
одной инерциальной системы отсчета относительно другой, если скорость частицы относительно одной системы  =0,5с, а ее же скорость относительно другой инерциальной системы отсчета
=0,5с, а ее же скорость относительно другой инерциальной системы отсчета 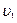 =0,3с, где с – скорость света в вакууме.
=0,3с, где с – скорость света в вакууме.
 Дано: Дано:
 =0,5с =0,5с
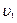 =0,3с
с = =0,3с
с = 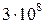 м/с м/с

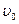 =? =?
| Решение:
Примем одну из инерциальных систем отсчета, относительно которой скорость частицы равна  , за неподвижную. Тогда вторая система отсчета движется относительно первой со скоростью , за неподвижную. Тогда вторая система отсчета движется относительно первой со скоростью 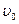 , а частица движется относительно второй системы отсчета со скоростью , а частица движется относительно второй системы отсчета со скоростью 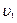 . .
|
| Согласно правилу преобразования релятивистских скоростей
Отсюда найдем скорость Ответ: | |
5.Три частицы движутся в одном направлении вдоль одной прямой в инерциальной системе отсчета. Скорость первой частицы относительно второй 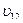 =0,2с, скорость второй частицы относительно третей
=0,2с, скорость второй частицы относительно третей 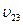 =0,5с. Скорость третей частицы относительно этой системы отсчета
=0,5с. Скорость третей частицы относительно этой системы отсчета 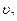 =0,7с. Чему равны скорости первой частицы
=0,7с. Чему равны скорости первой частицы 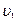 и второй
и второй 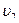 относительно системы отсчета, в которой они движутся?
относительно системы отсчета, в которой они движутся?
 Дано: Дано:
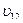 =0,2с =0,2с
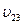 =0,5с =0,5с
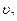 =0,7с =0,7с

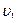 =? =?
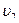 =? =?
| Решение:
Скорость второй частицы относительно системы отсчета согласно правилу
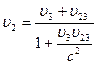 или с учетом условия задачи
или с учетом условия задачи
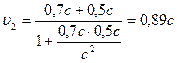
|
.
Зная абсолютную скорость второй частицы 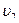 и скорость первой частицы относительно второй, определим по той же формуле скорость первой частицы
и скорость первой частицы относительно второй, определим по той же формуле скорость первой частицы 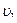 относительно системы отсчета:
относительно системы отсчета:
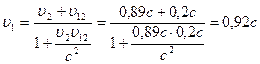 .
.
Ответ: 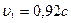 ,
, 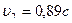 .
.
Задачи для самостоятельного решения
1. Две элементарные частицы движутся навстречу друг другу с относительной скоростью  =0,8с. Скорость одной из них относительно лабораторной системы отсчета
=0,8с. Скорость одной из них относительно лабораторной системы отсчета 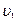 =0,4с. Чему равна скорость
=0,4с. Чему равна скорость 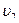 другой частицы относительно этой системы отсчета? (Ответ:
другой частицы относительно этой системы отсчета? (Ответ: 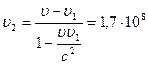 м/с).
м/с).
2. На каком расстоянии S друг от друга находились сначала две частицы, движущиеся со скоростями 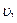 =0,2с и
=0,2с и 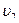 =0,6с, если время их сближения составило
=0,6с, если время их сближения составило 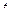 = 10 мкс (Ответ:
= 10 мкс (Ответ: 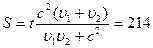 м).
м).
3. Три частицы движутся в одном направлении вдоль одной прямой в инерциальной системе отсчета. Скорость первой частицы относительно этой системы отсчета 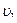 =0,4с, скорость первой частицы относительно второй
=0,4с, скорость первой частицы относительно второй 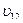 =0,6с, а скорость второй частицы относительно третей
=0,6с, а скорость второй частицы относительно третей 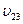 =0,8с. Чему равны скорости
=0,8с. Чему равны скорости 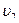 и
и 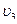 второй и третей частиц относительно этой системы отсчета? (Ответ:
второй и третей частиц относительно этой системы отсчета? (Ответ: 
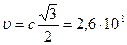 м/с).
м/с).
4. Элементарная частица – мезон – «живет» по его «собственным» часам 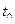 =1 с. Какое время
=1 с. Какое время 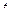 живет мезон по земным часам, если он движется относительно земного наблюдателя со скоростью
живет мезон по земным часам, если он движется относительно земного наблюдателя со скоростью  = 0,9с? (Ответ:
= 0,9с? (Ответ: 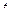 =1,05 ).
=1,05 ).
5. Найти собственную длину стержня 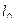 в космическом корабле, движущемся со скоростью
в космическом корабле, движущемся со скоростью  =0,6с, если его длина относительно неподвижной системы отсчета
=0,6с, если его длина относительно неподвижной системы отсчета 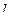 =10 см. (Ответ:
=10 см. (Ответ: 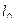 =12,5 см).
=12,5 см).
6. При какой скорости  длина тела сокращается на 25%? (Ответ:
длина тела сокращается на 25%? (Ответ:  =0,66с=
=0,66с= 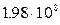 м/с).
м/с).
Дата: 2018-12-28, просмотров: 972.
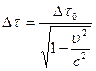 . Отсюда
. Отсюда 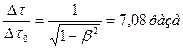 .
.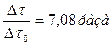
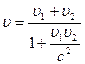 .
.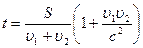 .
.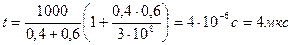 .
.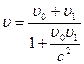 .
.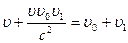 ,
, 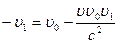 , откуда
, откуда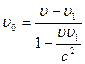
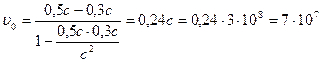 м/с.
м/с.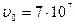 м/с.
м/с.