Чаcть I
Уфа 2009
УДК 539.19 (075.3)
ББК 22.36я
Ф 27
Фатыхов М.А. Механика. Молекулярная физика и термодинамика: Методическое пособие по решению задач. Часть I. – Уфа: Изд-во БГПУ им. М.Акмуллы, 2009. – 79 с.
Пособие по курсу общей физика включает основные теоретические сведения, примеры решения задач и задачи для самостоятельного решения на практических занятиях по разделам « Механика. Молекулярная физика и термодинамика » .
Пособие предназначено студентам педагогического университета нефизических специальностей.
Рецензенты:
.
Введение
Преподавание курса общей физики в университете опирается на взаимосвязь лекций, практических занятий и лабораторного практикума.
Практические занятия являются важнейшей компонентой учебного процесса. Они учат студентов анализировать изучаемые физические явления, использовать на практике полученные теоретические знания и приобщают студентов к самостоятельной работе.
Курс общей физики, включающий несколько разделов, на нефизических специальностях проходят в течение трех семестров. Являясь Авиически первыми двумя разделами, изучение курса общей физики начинается с механики, молекулярной физики и термодинамики. Данное методическое пособие предназначено в помощь студентам на практических Авииях при решении задач по этим разделам. В нём приведены основные формулы, облегчающие усвоение алгоритмов решения типичных задач разной степени сложности, сопровождаемые необходимыми комментариями и задачи для самостоятельного решения.
Основной задачей данного методического пособия является привитие студентам навыков самостоятельного изучения физики. Предлагаемый в нем материал содержит изложение основных вопросов, знание которых должно способствовать изучению курса общей физики.
При работе с пособием студентам рекомендуется ознакомиться с примерами решения задач, затем решить задачи для самостоятельной работы и сверить ответы.
Механика
5. Кинематика поступательного движения материальной точки
Основные формулы
Скорость прямолинейного движения в общем случае равна: 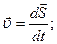
Ускорение прямолинейного движения в общем случае равно: 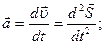
В случае прямолинейного равномерного движения: 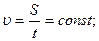
В случае прямолинейного равноускоренного движения: 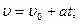
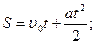 а= const .
а= const .
В этих уравнениях ускорение 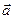 положительно при равноускоренном движении и отрицательно – при равнозамедленном.
положительно при равноускоренном движении и отрицательно – при равнозамедленном.
При криволинейном движении полное ускорение равно: 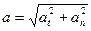 , где
, где 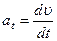 ;
; 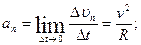
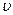 – скорость движения, R – радиус кривизны траектории в данной точке.
– скорость движения, R – радиус кривизны траектории в данной точке.
Примеры решения задач
Прямолинейное равномерное движение
5. Половину времени своего движения автомобиль ехал со скоростью 100 км/ч, оставшуюся половину времени – со скоростью 20 км/ч. Найти среднюю скорость движения.
 Дано: Дано:
 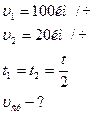
| Решение: Средняя скорость движения: 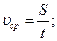
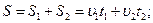
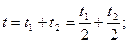
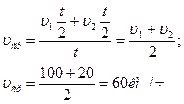
|
Ответ: 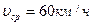 , вполне удовлетворяет условию задачи.
, вполне удовлетворяет условию задачи.
2. Половину пути автомобиль ехал со скоростью 100 км/ч, оставшуюся половину пути – со скоростью 20 км/ч. Найти среднюю скорость движения.
 Дано: Дано:
 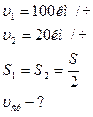
| Решение:
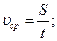
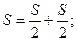
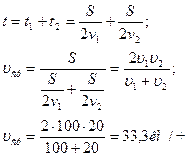
|
Ответ: 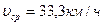 .
.
3. На лодке переплывают реку, отправляясь из пункта А (см. рисунок). Скорость лодки в стоячей воде 5 м/с, скорость течения реки u =3 м/с, ширина реки S=200 м. а). В какой точке лодка пристанет к противоположному берегу, если держать курс перпендикулярно берегам? Б). Какой курс следует держать, чтобы попасть в точку В? Для обоих случаев найдите время переправы.

Дано:
 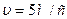
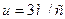
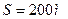
 a )
a ) 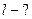 б)
б) 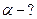
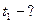
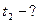
| Решение:
а). Скорость лодки 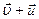 относительно берега будет направлена под углом к отрезку АВ (см. рисунок а). За время переправы лодку снесет вниз по течению на расстояние l, которое можно найти, пользуясь подобием треугольника скоростей и треугольника АВС: относительно берега будет направлена под углом к отрезку АВ (см. рисунок а). За время переправы лодку снесет вниз по течению на расстояние l, которое можно найти, пользуясь подобием треугольника скоростей и треугольника АВС:
|
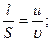
Откуда 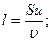
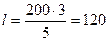 м.
м.
Течение реки в этом случае вообще не влияет на время переправы:
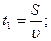
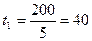 с.
с.
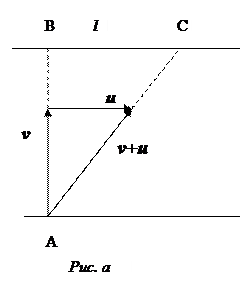
Б). Следует держать курс под углом 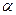 к отрезку АВ (см. рисунок б),
к отрезку АВ (см. рисунок б),
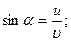
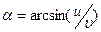 ;
;
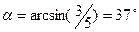 ;
;
Скорость v 1  должна быть направлена под углом к отрезку АВ, чтобы компенсировать боковой снос. Модуль скорости
должна быть направлена под углом к отрезку АВ, чтобы компенсировать боковой снос. Модуль скорости 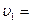
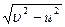 .
.
Время переправы в этом случае 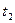
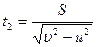 ;
;
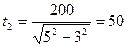 с.
с.
Заметим, что переправа при этом случае занимает больше времени, хотя и происходит по кратчайшему пути.
Ответ: t 1 =40 c , t 2 =50 c , 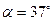 .
.
Криволинейное движение
4. Два тела падают без начальной скорости с одной и той же высоты Н. На пути второго тела находится расположенная под углом 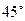 к горизонту площадка, с которой тело упруго сталкивается. Какое тело падало дольше? У какого тела больше конечная скорость? На какой высоте надо разместить площадку, чтобы второе тело упало как можно позже?
к горизонту площадка, с которой тело упруго сталкивается. Какое тело падало дольше? У какого тела больше конечная скорость? На какой высоте надо разместить площадку, чтобы второе тело упало как можно позже?
 Дано: Дано:
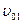 = 0 м/с = 0 м/с
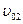 = 0 м/с
Н = 0 м/с
Н
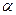 =450 =450
t =?
h=?
|  
   

 Решение: Решение:
|
Время движения второго тела максимально, если площадка
находится на высоте 0,5Н.
Первое тело движется прямолинейно равноускоренно, следовательно:
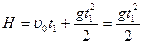 , тогда
, тогда
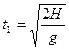 .
.
В случае прямолинейного равноускоренного движения 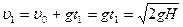 .
.
Время падения и конечная скорость первого тела
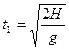 ;
; 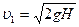 .
.
Скорость второго тела после столкновения (см. рисунок) направлена горизонтально, т.е. 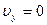 . Поскольку в момент соударения гасится вертикальная скорость тела, время падения увеличивается. Пусть площадка расположена на высоте h. К моменту удара о площадку
. Поскольку в момент соударения гасится вертикальная скорость тела, время падения увеличивается. Пусть площадка расположена на высоте h. К моменту удара о площадку
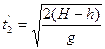 ,
, 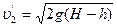 .
.
Полное время падения второго тела
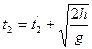 , так что
, так что
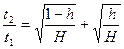 .
.
Это отношение больше единицы, поскольку 
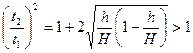 .
.
При  или
или  получаем, что
получаем, что 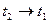 . Наибольшая «задержка» падения второго тела происходит при этом
. Наибольшая «задержка» падения второго тела происходит при этом 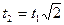 . Тело 2 упадет позже, чем тело 1.Вопрос о конечности скорости второго тела можно теперь сформулировать так: с какой скоростью
. Тело 2 упадет позже, чем тело 1.Вопрос о конечности скорости второго тела можно теперь сформулировать так: с какой скоростью 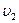 упадет тело, брошенное горизонтально со скоростью
упадет тело, брошенное горизонтально со скоростью 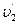 с высоты h? Для ответа на этот вопрос рассмотрим проекции скорости тела 2 на оси координат:
с высоты h? Для ответа на этот вопрос рассмотрим проекции скорости тела 2 на оси координат:
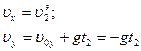
Поэтому:
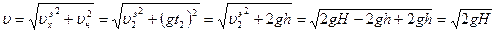 .
.
Итак, 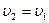 , т.е. оба тела упадут с одинаковой по модулю скоростью.
, т.е. оба тела упадут с одинаковой по модулю скоростью.
Ответ: h=H/2, 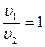 ,
, 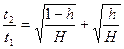 .
.
5. Снаряд вылетает из пушки с начальной скоростью 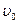 =1000 м/с под углом к горизонту
=1000 м/с под углом к горизонту 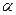 =300. Какое время
=300. Какое время 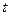 снаряд находится в воздухе? На какую высоту H поднимается? На каком расстоянии L от пушки он упадет на землю?
снаряд находится в воздухе? На какую высоту H поднимается? На каком расстоянии L от пушки он упадет на землю?
 Дано: Дано:
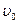 =1000 м/с =1000 м/с
 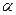 =300
Н=?
L =?
T =? =300
Н=?
L =?
T =?
| Решение:
Движение вдоль оси OY – равноускоренное, вдоль оси OX – равномерное:
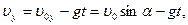
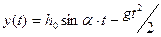 ; ;
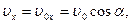 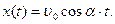 (1)
Время подъема определим из условия: (1)
Время подъема определим из условия: 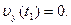 
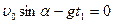 ;
Время полета равно: ;
Время полета равно: 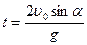 ; ;
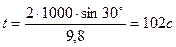
|

Из выражения (1) выразим t :
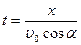 , подставим в выражение для
, подставим в выражение для 
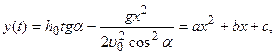
т.е. траектория движения – парабола, координаты вершины 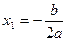 .
.
Это и есть максимальная высота подъема, следовательно, тело поднимется на высоту: 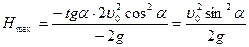 ;
;
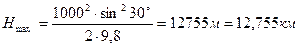 .
.
Найдем дальность полета по формуле: 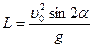 ;
;
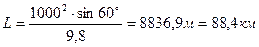 .
.
Ответ: H=12,75 км, L=88,4 км, t=102 c.
Задачи для самостоятельного решения
1. Координата материальной точки, движущейся вдоль оси х, задана формулой х=7-3t + t 2. Какова формула зависимости скорости точки от времени? (Ответ:  =-3+2 t)
=-3+2 t)
2. Автомобиль проехал половину пути со скоростью  км/ч. Следующий отрезок пути он ехал со скоростью
км/ч. Следующий отрезок пути он ехал со скоростью 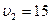 км/ч, а последний отрезок пути – со скоростью
км/ч, а последний отрезок пути – со скоростью 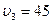 км/ч. Какова средняя скорость автомобиля, если второй и третий отрезки пройдены за одинаковое время?(
км/ч. Какова средняя скорость автомобиля, если второй и третий отрезки пройдены за одинаковое время?( 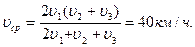 ).
).
3. Лыжник скатился с горы длиной s1= 60 м за t1=15 с, а затем проехал по горизонтальному участку еще s2=30 м до остановки. На обоих участках движение было равноускоренным. Найдите скорость 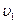 лыжника в конце спуска и ускорение a 2 на горизонтальном участке. Постройте график зависимости скорости от времени.(Ответ:
лыжника в конце спуска и ускорение a 2 на горизонтальном участке. Постройте график зависимости скорости от времени.(Ответ: 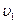 =8м/с, a 2 =-1,1 м/с2).
=8м/с, a 2 =-1,1 м/с2).
4. Моторная лодка проходит расстояние между двумя пунктами А и В по течению реки за время t1=3 ч, а плот – за время t=12 ч. Сколько времени t2 затратит моторная лодка на обратный путь? (Ответ: 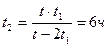 ).
).
5. Два автомобиля движутся с постоянными скоростями 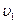 и
и 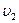 по дорогам, пересекающимся под прямым углом. Когда первый автомобиль достиг перекрестка, второму оставалось проехать до этого Авта расстояние l . Спустя какое время t после этого расстояние между автомобилями будет наименьшим? Чему равно это расстояние smin? (Ответ:
по дорогам, пересекающимся под прямым углом. Когда первый автомобиль достиг перекрестка, второму оставалось проехать до этого Авта расстояние l . Спустя какое время t после этого расстояние между автомобилями будет наименьшим? Чему равно это расстояние smin? (Ответ: 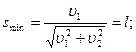
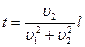 ).
).
6. Лодка движется перпендикулярно к берегу со скоростью 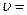 7,2 км/ч. Течение относит ее вниз на расстояние l =150 м. Найти скорость u течения реки и время t, затраченное на переправу. Ширина реки L=0,5 км. (Ответ: u =0,60 м/с, t=250 c).
7,2 км/ч. Течение относит ее вниз на расстояние l =150 м. Найти скорость u течения реки и время t, затраченное на переправу. Ширина реки L=0,5 км. (Ответ: u =0,60 м/с, t=250 c).
7. Тело падает с высоты h =19,6 м без начальной скорости. Какой путь пройдет тело за n -ую секунду своего падения, за последнюю секунду? За какое время тело пройдет n -ый метр своего пути, последний метр? (Ответ: 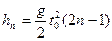 , где
, где 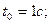
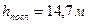 ,
, 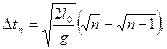
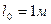 ,
, 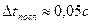 ).
).
8. Мяч брошен со скоростью 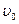 под углом
под углом 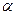 к горизонту. Найти
к горизонту. Найти 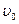 и
и 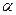 , если максимальная высота подъема мяча h =3м, а радиус кривизны траектории мяча в этой точке R=3м.(Ответ: tg
, если максимальная высота подъема мяча h =3м, а радиус кривизны траектории мяча в этой точке R=3м.(Ответ: tg 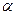 =
= 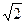 ,
, 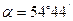 ;
; 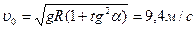 ).
).
9. Под углом 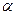 =60
=60 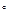 к горизонту брошено тело с начальной скоростью
к горизонту брошено тело с начальной скоростью 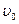 =20м/с. Через какое время t модуль
=20м/с. Через какое время t модуль 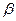 угла между скоростью тела и горизонтальной плоскостью равен 45
угла между скоростью тела и горизонтальной плоскостью равен 45 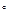 ? (Ответ: t1=0,75 с, t2=2,8 с.
? (Ответ: t1=0,75 с, t2=2,8 с.
10. На рисунке приведен график зависимости 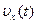 для тела, Авииегося вдоль оси х. Постройте графики зависимости от времени ускорения a х , перемещения s х и пройденного пути l .
для тела, Авииегося вдоль оси х. Постройте графики зависимости от времени ускорения a х , перемещения s х и пройденного пути l .
2. Кинематика вращательного движения
Материальной точки
Основные формулы
При вращательном движении, в общем случае, угловая скорость равна 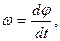 где
где 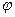 - угол поворота.
- угол поворота.
В случае равномерного вращательного движения тела угловая скорость равна 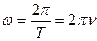 , где
, где 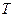 - период обращения,
- период обращения, 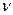 - частота обращения. Угловое ускорение равно
- частота обращения. Угловое ускорение равно 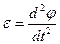 . Угловая скорость связана с линейной скоростью соотношением
. Угловая скорость связана с линейной скоростью соотношением 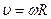 . Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены следующим образом:
. Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены следующим образом: 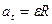 и
и 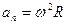 . Полное ускорение можно выразить следующим образом
. Полное ускорение можно выразить следующим образом 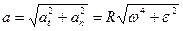 .
.
Примеры решения задач
5. Колесо радиусом 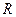 =0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением
=0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 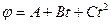 , где В=2 рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t=2 с после начала движения: а) угловую скорость
, где В=2 рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t=2 с после начала движения: а) угловую скорость 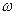 , б)линейную скорость
, б)линейную скорость 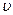 , в) угловое ускорение
, в) угловое ускорение 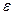 , г) тангенциальное
, г) тангенциальное 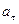 , нормальное
, нормальное 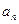 ускорения, д) полное ускорение а
ускорения, д) полное ускорение а
Дано:
 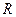 =0,1 м =0,1 м
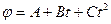 В=2 рад/с
С=1 рад/с3
t =2 с
В=2 рад/с
С=1 рад/с3
t =2 с
а) Б) В) Г)
| Решение:
а) Угловая скорость вращения колеса 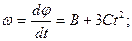
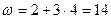 рад/с.
Б) Линейная скорость рад/с.
Б) Линейная скорость 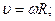 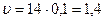 м/с.
В) Угловое ускорение м/с.
В) Угловое ускорение 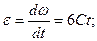
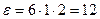 рад/с2.
Г) Нормальное ускорение рад/с2.
Г) Нормальное ускорение 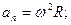  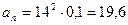 м/с2.
Тангенциальное ускорение м/с2.
Тангенциальное ускорение 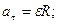 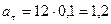 м/с2.
Д) Полное ускорение м/с2.
Д) Полное ускорение 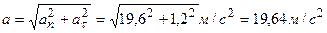 . .
|
Ответ: а) 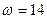 рад/с, б)
рад/с, б) 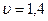 м/с, в)
м/с, в) 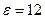 рад/с2, г)
рад/с2, г) 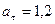 м/с2,
м/с2, 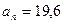 м/с2, д)
м/с2, д) 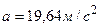 .
.
2. Найти радиус вращающегося колеса, если известно, что линейная скорость 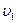 точки, лежащей на ободе, в 2,5 раза больше линейной скорости
точки, лежащей на ободе, в 2,5 раза больше линейной скорости 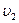 точки, лежащей на расстоянии r=5 см ближе к оси колеса.
точки, лежащей на расстоянии r=5 см ближе к оси колеса.
 Дано: Дано:
 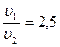 R= ?
R= ?
| Решение:
Угловая скорость связана с линейной скоростью
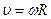 ;
Тогда ;
Тогда
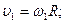
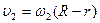 ; ;
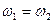 , следовательно, , следовательно, 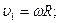 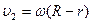 ;
Найдем отношение ;
Найдем отношение 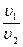 : :
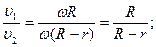
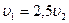 , тогда , тогда
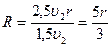 ; ;
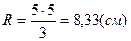 .
Ответ:R=8,33(см). .
Ответ:R=8,33(см).
|
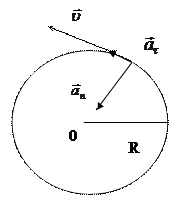
3. Точка движется по окружности радиусом R=2 см. Зависимость пути от времени дается уравнением 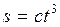 , где с=0,1 см/с
, где с=0,1 см/с 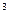 . Найти нормальное
. Найти нормальное 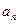 и тангенциальное
и тангенциальное 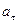 ускорение точки в момент, когда линейная скорость точки
ускорение точки в момент, когда линейная скорость точки 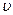 =0,3 м/с.
=0,3 м/с.
Дано:
 R =2 см=0,02 м R =2 см=0,02 м
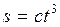 с=0,1 см/с
с=0,1 см/с 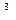 =0,001м/с3 =0,001м/с3
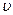 =0,3 м/с =0,3 м/с
 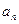 =? =?
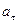 =? =?
|
Решение:
Скорость точки можно найти как производную пути по времени:
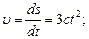 (1)
Тангенциальное ускорение этой точки находится как производная линейной скорости по времени: (1)
Тангенциальное ускорение этой точки находится как производная линейной скорости по времени:
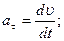 (2) (2)
|
Подставим выражение (1) в (2). Получим:
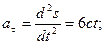 (3)
(3)
Найдем время t когда 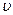 =0,3 м/с:
=0,3 м/с:
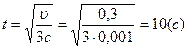
Найденное значение t подставим в выражение (3):
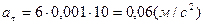 .
.
Нормальное ускорение при криволинейном движении выражается через скорость материальной точки и радиус кривизны траектории:
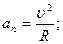
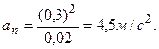 .
.
Ответ: 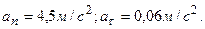
Задачи для самостоятельного решения
1. Колесо радиусом R=5 см вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 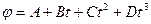 , где D=1 рад/с3. Для точек, лежащих на ободе колеса, найти изменение тангенциального ускорения
, где D=1 рад/с3. Для точек, лежащих на ободе колеса, найти изменение тангенциального ускорения 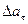 за единицу времени. (Ответ:
за единицу времени. (Ответ: 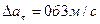 ).
).
2. Колесо, вращаясь равноускоренно, достигло угловой скорости 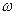 =20 рад/с через n=10 оборотов после начала вращения. Найти угловое ускорение
=20 рад/с через n=10 оборотов после начала вращения. Найти угловое ускорение 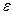 колеса. (Ответ:
колеса. (Ответ: 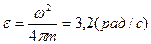 ).
).
3. Вал вращается с частотой n=180 об/мин. С некоторого момента вал начинал вращаться равнозамедленно с угловым ускорением 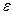 =3 рад/с
=3 рад/с 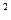 . Через какое время t вал остановится? Найти число оборотов вала n до остановки. (Ответ: t =6,3 с, n =9,4 об).
. Через какое время t вал остановится? Найти число оборотов вала n до остановки. (Ответ: t =6,3 с, n =9,4 об).
4. Точка движется по окружности радиуса R =20 см с постоянным тангенциальным ускорением 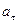 =5 см/с
=5 см/с 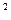 . Через какое время t после начала движения нормальное ускорение
. Через какое время t после начала движения нормальное ускорение 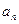 точки будет: а) равно тангенциальному, б) вдвое больше тангенциального? (Ответ:
точки будет: а) равно тангенциальному, б) вдвое больше тангенциального? (Ответ: 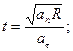 а)
а) 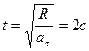 б)
б) 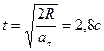 ).
).
5. Две точки М1 и М2 движутся по одной окружности в одну сторону согласно уравнениям 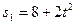 и
и 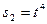 , где путь s выражен в сантиметрах, а время t – в секундах, началом отсчета расстояний s 1 и s 2 служит одна точка. Определить время первой встречи обеих точек и значения их скоростей и ускорений в тот момент, если радиус окружности равен 16 см. (Ответ:
, где путь s выражен в сантиметрах, а время t – в секундах, началом отсчета расстояний s 1 и s 2 служит одна точка. Определить время первой встречи обеих точек и значения их скоростей и ускорений в тот момент, если радиус окружности равен 16 см. (Ответ: 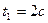 ,
, 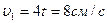 ,
, 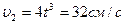 ,
, 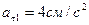 ,
, 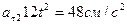 ,
, 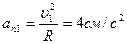 ,
, 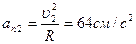 ,
, 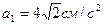 ,
, 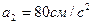 ).
).
6. В модели атома Бора электрон в атоме водорода движется по круговой орбите с линейной скоростью 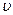 . Найти угловую скорость
. Найти угловую скорость 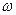 вращения электрона вокруг ядра и его нормальное ускорение
вращения электрона вокруг ядра и его нормальное ускорение 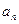 . Считать радиус орбиты
. Считать радиус орбиты 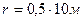 и линейную скорость на этой орбите
и линейную скорость на этой орбите 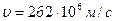 . (Ответ:
. (Ответ: 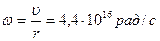 ,
, 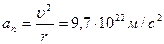 ).
).
Дата: 2018-12-28, просмотров: 465.

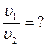

 =?
=?  =?
=?