Основные формулы
Момент 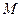 силы
силы  относительно какой-нибудь оси вращения определяется формулой
относительно какой-нибудь оси вращения определяется формулой
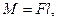
где 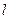 - расстояние от оси вращения до прямой, вдоль которой действует сила.
- расстояние от оси вращения до прямой, вдоль которой действует сила.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра
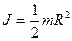 ,
,
где 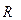 - радиус цилиндра,
- радиус цилиндра, 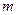 - его масса.
- его масса.
Момент инерции полого однородного цилиндра (обруча) относительно оси цилиндра
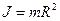 .
.
Момент инерции однородного шара радиуса 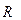 относительно оси, проходящей через его центр,
относительно оси, проходящей через его центр,
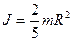 .
.
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно его длине 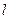 ,
,
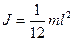 .
.
Если для какого-либо тела известен его момент инерции 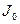 относительно оси, проходящей через его центр тяжести, то момент инерции относительно любой оси, параллельной первой, может быть найден по формуле Штейнера
относительно оси, проходящей через его центр тяжести, то момент инерции относительно любой оси, параллельной первой, может быть найден по формуле Штейнера
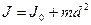 ,
,
где 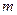 - масса тела,
- масса тела, 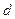 - расстояние от центра тяжести тела до оси вращения.
- расстояние от центра тяжести тела до оси вращения.
Основной закон динамики вращательного движения при 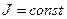 имеет вид
имеет вид
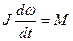 или
или 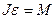 ,
,
где 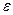 - угловое ускорение, приобретаемое телом под действием вращающего момента
- угловое ускорение, приобретаемое телом под действием вращающего момента 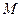 ,
, 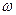 - угловая скорость вращения тела.
- угловая скорость вращения тела.
Кинетическая энергия вращающегося тела
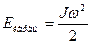 ,
,
где 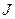 - момент инерции тела,
- момент инерции тела, 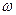 - его угловая скорость.
- его угловая скорость.
Примеры решения задач
1. Через неподвижный блок в виде однородного цилиндра массой m=160 г перекинута невесомая нить, к концам которой подвешены грузы массами m1=200 г и m2=300 г. Пренебрегая трением в оси блока, определить: 1) ускорение a грузов; 2) силы натяжения T1 и T2 грузов.
 Дано:
m=160 г=0,16 кг
m 1 =200 г=0,2 кг
m 2 =300 г=0,3 кг Дано:
m=160 г=0,16 кг
m 1 =200 г=0,2 кг
m 2 =300 г=0,3 кг
 a=?
T1=?
T2=?
a=?
T1=?
T2=?
| Решение:
Направим ось ox вертикально вниз, запишем для каждого груза уравнение движения (второй закон Ньютона) в проекции на эту ось:
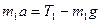 , ,
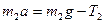 , ,
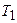 и и 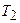 неодинаковы, т.к. неодинаковы, т.к. 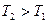 : за счет этого обеспечивается вращательный момент, действующий на блок. : за счет этого обеспечивается вращательный момент, действующий на блок.
|
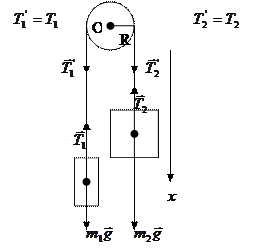
Согласно основному закону динамики вращательного движения, вращающий момент, приложенный к цилиндру,
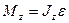 . (1)
. (1)
С другой стороны:
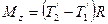 , (2)
, (2)
R – плечо силы, равное радиусу цилиндра.
По третьему закону Ньютона, с учетом невесомости нити имеем:
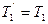 и
и 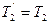 . Воспользовавшись этим и приравняв (1) и (2), получим:
. Воспользовавшись этим и приравняв (1) и (2), получим:
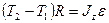 ,
,
где 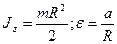 .
.
Получим,
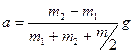 .
.
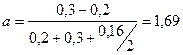 м/с2.
м/с2.
Зная a, найдем T1 и T2:
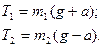
Подставив данные нам значения, найдем силы натяжения нити:
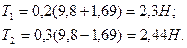
Ответ: 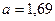 м/с2, T 1 =2,3 H , T 2 =2,44 H.
м/с2, T 1 =2,3 H , T 2 =2,44 H.
2. Однородный стержень длиной 1 м и массой 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если на него действует момент силы 98,1 мН∙м2
 Дано:
m=0,5 кг Дано:
m=0,5 кг
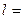 1 м
М = 98,1 мН∙м2 1 м
М = 98,1 мН∙м2

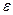 =? =?
| Решение:
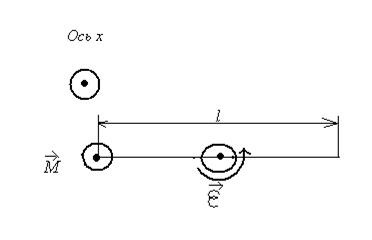 Запишем уравнение вращательного движения стержня в проекции на ось х:
Запишем уравнение вращательного движения стержня в проекции на ось х:
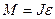 .
Отсюда .
Отсюда 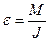 .
Момент инерции стержня относительно оси, проходящей через середину, .
Момент инерции стержня относительно оси, проходящей через середину,
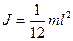 .
Тогда .
Тогда 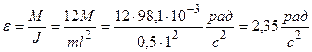 .
Ответ: .
Ответ: 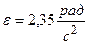 . .
|

3. Шар массой 1 кг катится без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку - 10 м/с, после удара – 8 м/с. Найти количество тепла, выделившееся при ударе шара о стенку.
 Дано:
m=1 кг
v = 10 c м/с
u =8 см/с Дано:
m=1 кг
v = 10 c м/с
u =8 см/с
 Q=?
Q=?
| Решение:
Будем считать, что движение происходит в горизонтальной плоскости. Обозначим через 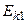 кинетическую энергию шара до удара. Она складывается из кинетической энергии поступательного движения кинетическую энергию шара до удара. Она складывается из кинетической энергии поступательного движения 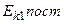 и кинетической энергии вращения и кинетической энергии вращения 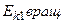 : : 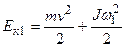 Для шара момент инерции
Для шара момент инерции 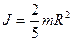 , а угловая скорость , а угловая скорость 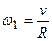 .
Обозначим через .
Обозначим через 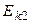 кинетическую энергию шара после удара. Аналогично кинетическую энергию шара после удара. Аналогично 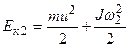 , где , где 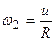 . Тогда количество тепла Q равно убыли кинетической энергии . Тогда количество тепла Q равно убыли кинетической энергии
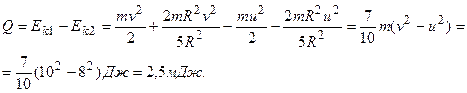 Ответ:
Ответ: 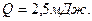
|
3. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы с частотой 10 об/мин. Человек массой 60 кг стоит при этом на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека – точечной массой.
 Дано: Дано:
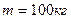
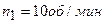
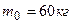

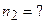
| Решение:
| ||
|
где
Обозначим через R радиус платформы. Определим моменты инерции:
Также имеем: Подставляя их в предыдущие формулы, имеем Отсюда следует решение задачи:
Ответ: | |||
4. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) – одинакового радиуса 6 см и одинаковой массы 0,5 кг. Найти моменты инерции этих цилиндров.
Дано:
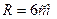
 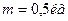
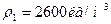
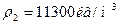
 J1=? J2=? J1=? J2=?
| Решение:
Момент инерции алюминиевого цилиндра
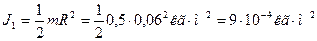 .
Момент инерции свинцового цилиндра .
Момент инерции свинцового цилиндра
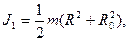 где R 0 – внутренний радиус свинцового цилиндра. Найдем его. где R 0 – внутренний радиус свинцового цилиндра. Найдем его.
|
| Обозначим через Тогда момент инерции свинцового цилиндра
Ответ: | |
Задачи для самостоятельного решения
1. Горизонтальная платформа массой m=100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой  =10 об/мин. Человек массой
=10 об/мин. Человек массой  =60 кг стоит при этом на краю платформы. С какой частотой
=60 кг стоит при этом на краю платформы. С какой частотой 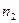 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. (Ответ:
начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. (Ответ: 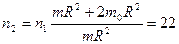 об/мин).
об/мин).
2. Определите момент инерции сплошного однородного диска радиусом R=40 см и массой m=1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. (Ответ: J =0,12 кг’м2).
3. Шар радиусом R=10 см и массой m=5 кг вращается вокруг оси согласно уравнению 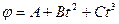 (
( 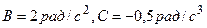 ). Определите момент сил M для t=3 c. (Ответ:
). Определите момент сил M для t=3 c. (Ответ: 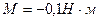 ).
).
4. На однородный сплошной цилиндрический вал радиусом R=50 см намотана легкая нить, к концу которой прикреплен груз массой m=6,4 кг. Груз, разматывая нить, опускается с ускорением a=2 м/с2. Определите: 1) момент инерции J вала; 2) массу M вала. (Ответ: J=6,25 кг м2, M=50 кг).

5. Через неподвижный однородный блок в виде однородного сплошного цилиндра массой m=0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m1=0,35 кг и m2=0,55 кг. Пренебрегая трением в оси блока, определить: 1) ускорение a грузов; 2) отношение 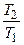 сил натяжения нити. (Ответ: 1)
сил натяжения нити. (Ответ: 1) 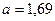 м/с2,
м/с2, 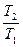 =1,05).
=1,05).
6. Какую работу совершает человек при переходе от края платформы к ее центру в условиях задачи 4.3? Радиус платформы равен 1,5 м. (Ответ: (Ответ: А= 162 Дж).
7. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска. (Ответ: Ек= 24 Дж).
Работа и энергия
Основные формулы
Работа силы при перемещении тела может быть выражена следующей формулой 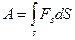 , где
, где 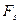 - проекция силы на направление пути,
- проекция силы на направление пути, 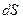 - величина участка пути. Интегрирование должно быть распространено на весь путь S. В частном случае постоянной силы, действующей под неизменным углом к перемещению, имеем
- величина участка пути. Интегрирование должно быть распространено на весь путь S. В частном случае постоянной силы, действующей под неизменным углом к перемещению, имеем
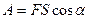 ,
,
где 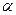 - гол между силой и перемещением.
- гол между силой и перемещением.
Работа при упругой деформации определяется формулой
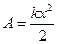 ,
,
где k – коэффициент жесткости пружины.
Работа, совершаемая системой равна изменению энергии системы:
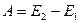 .
.
Полная механическая энергия системы тел равна сумме ее кинетической и потенциальной энергий:
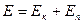 .
.
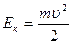 ,
,
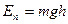 .
.
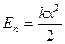 .
.
Примеры решения задач
1. Какая минимальная работа А совершается при подъеме на крышу веревки длиной l=40 м и массой m=6 кг? В начальный момент вся веревка свешивалась вертикально с края крыши.
 Дано:
l=40 м
m =6 кг
А=? Дано:
l=40 м
m =6 кг
А=? 
| Решение:
1). В тот момент, когда длина вытянутой части веревки равна x, для равномерного подъема
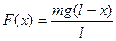 .
Работа, совершаемая при изменении x от 0 до l, численно равна площади по графику F ( x ): .
Работа, совершаемая при изменении x от 0 до l, численно равна площади по графику F ( x ):
|
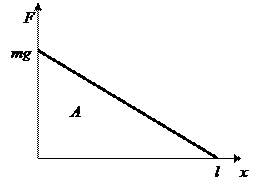
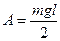 ;
;
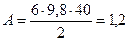 кДж.
кДж.
2). Можно вычислить работу по подъему тела следующим образом:
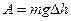 ,
,
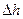 - изменение высоты центра тяжести тела (в данном случае
- изменение высоты центра тяжести тела (в данном случае 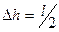 ).
).
Ответ: 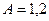 кДж.
кДж.
2. Камень массой М=10 кг поднимают на высоту h=10 м, прикладывая постоянную силу F=200 H. Какую работу совершает эта сила? Чему равно изменение потенциальной энергии 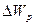 ?
?
 Дано:
М=10 кг
h =10 м
F =200 H Дано:
М=10 кг
h =10 м
F =200 H

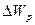 =? =?
| Решение:
Камень при подъеме приобретает, помимо потенциальной энергии, кинетическую энергию 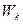 , так что , так что 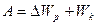 . .
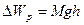
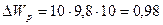 кДж кДж
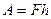 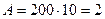 кДж.
Ответ: кДж.
Ответ: 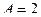 кДж. кДж.
|
3. Мяч радиусом 10 см плавает в воде т так, что его центр масс находится на 9 см выше поверхности воды. Какую работу надо совершить, чтобы погрезить мяч в воду до диаметральной плоскости?
 Дано:
R =10 c м
Н=9 см
Дано:
R =10 c м
Н=9 см
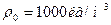 А=?
А=?
|
Решение:
|
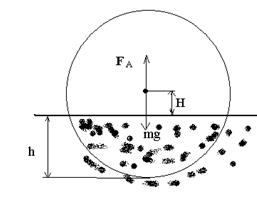
| На рисунке указаны силы, действующие на мяч:
Здесь Очевидно, что Погрузим мяч в воду на глубину х под действием силы
где сила Архимеда в этом случае имеет вид
Следовательно, Здесь Как видно из двух последних формул, сила является переменной от х, поэтому работа, которую надо совершить при погружении мяча до диаметральной плоскости будет
Ответ: 0,74 Дж. | |
4. Найти работу, которую надо совершить, чтобы сжать пружину на 20 см, если известно, что сила сжатия пропорциональна сжатию и жесткость пружины 2,94 кН/м.
  Дано:
L =20 см Дано:
L =20 см
 ~ l
k =2,94 кН/м
A=? ~ l
k =2,94 кН/м
A=?
| Решение:
Работа, совершаемая при сжатии пружины, определяется формулой
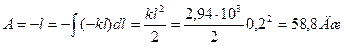 Ответ:
Ответ: 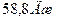
|
6. Автомобиль массой 2 т движется в гору с уклоном 4м на каждые 100 м пути. Коэффициент трения - 0,08. Найти работу, совершаемую двигателем на пути 3 км, и мощность, развиваемую двигателем, если известно, что этот путь был пройден за время, равное 4 мин.
Дано:
 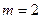 т т
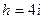
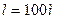
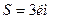
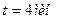

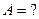
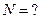
| Решение:
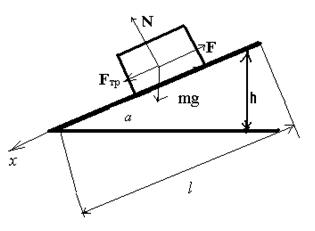
|
| В случае равномерного движения автомобиля Тогда согласно второму закону Ньютона сила тяги двигателя
Работа силы F на пути S
Мощность двигателя Ответ: | |
Задачи для самостоятельного решения
1. Санки массой M =20 кг поднимают по гладкому склону на высоту h=2,5 м, прикладывая силу F=120 Н, направленную вдоль склона. Санки движутся с ускорением 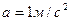 . Какую работу А совершает сила F при подъеме. Чему равно изменение потенциальной энергии
. Какую работу А совершает сила F при подъеме. Чему равно изменение потенциальной энергии 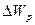 санок? Чему равна кинетическая энергия
санок? Чему равна кинетическая энергия 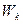 санок на вершине горы? (Ответ:
санок на вершине горы? (Ответ: 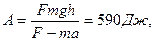
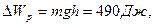
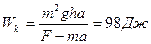 ).
).
2. Бассейн площадью S=100 м  заполнен водой до уровня h=2 м и разделен пополам подвижной вертикально перегородкой так, что она разделила площадь бассейна в отношении 1:3. Какую работу A пришлось при этом совершить? Вода не проникала через перегородку и не переливалась через край бассейна. (Ответ:
заполнен водой до уровня h=2 м и разделен пополам подвижной вертикально перегородкой так, что она разделила площадь бассейна в отношении 1:3. Какую работу A пришлось при этом совершить? Вода не проникала через перегородку и не переливалась через край бассейна. (Ответ: 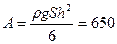 кДж).
кДж).
3. Вагон массой m=20 т, двигаясь равнозамедленно с начальной скоростью 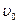 =54 км/ч, под действием силы трения F=6 кH через некоторое время останавливается. Найти работу силы трения и расстояние, которое вагон пройдет до остановки. (Ответ: A тр =2,25 МДж, S =375 м).
=54 км/ч, под действием силы трения F=6 кH через некоторое время останавливается. Найти работу силы трения и расстояние, которое вагон пройдет до остановки. (Ответ: A тр =2,25 МДж, S =375 м).
4. Шар диаметром 30 см плавает воде. Какую работу надо совершить, чтобы погрузить шар в воду на глубину 5 см глубже? Плотность материала шара 500 кг/м3.(Ответ: 0,84 Дж)
5. Какую мощность развивает двигатель автомобиля массой 1000 кг, если известно, что автомобиль едет с постоянной скоростью 36 км/ч: л) по горизонтальной дороге; б) в гору с уклоном 5 м на каждые 100м пути; в) под гору с тем же уклоном? Коэффициент трения равен 0,07.
(Ответ: 6,9 кВт, 11,8 кВт, 2 кВт).
Дата: 2018-12-28, просмотров: 493.
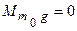 Следовательно, можно воспользоваться законом сохранения момента импульса. В проекции на ось
Следовательно, можно воспользоваться законом сохранения момента импульса. В проекции на ось 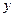
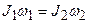 ,
,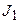 - момент инерции платформы с человеком, стоящим на ее краю;
- момент инерции платформы с человеком, стоящим на ее краю;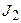 - момент инерции платформы с человеком, стоящим в центре,
- момент инерции платформы с человеком, стоящим в центре,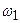 - угловое ускорение платформы в случае, когда человек стоит на краю платформы;
- угловое ускорение платформы в случае, когда человек стоит на краю платформы;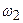 -угловое ускорение платформы в случае, когда человек стоит в центре платформы.
-угловое ускорение платформы в случае, когда человек стоит в центре платформы.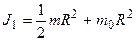 ,
, 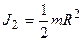 .
.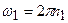 ,
, 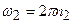 .
.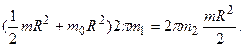
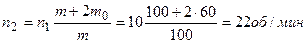 .
.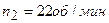 .
. длины цилиндров,
длины цилиндров,  - плотность алюминия,
- плотность алюминия, 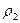 - плотность свинца. По условию массы обоих цилиндров равны. Поэтому
- плотность свинца. По условию массы обоих цилиндров равны. Поэтому 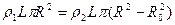 . Отсюда
. Отсюда 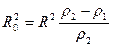 .
.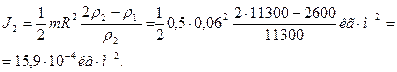
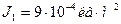 ,
, 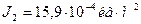
 - сила тяжести и
- сила тяжести и  - сила Архимеда. Мяч плавает, если эти силы равны, т.е.
- сила Архимеда. Мяч плавает, если эти силы равны, т.е. 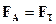 ,
, 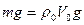 . (1)
. (1)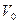 - объем шарового сегмента высотой h, находящегося в воде при равновесии, m- масса мяча.
- объем шарового сегмента высотой h, находящегося в воде при равновесии, m- масса мяча.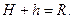
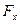 . Пусть при этом
. Пусть при этом 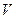 - объем шарового сегмента высотой h +х, находящегося в воде при равновесии. Тогда результирующая сила, выталкивающая мяч из воды, будет
- объем шарового сегмента высотой h +х, находящегося в воде при равновесии. Тогда результирующая сила, выталкивающая мяч из воды, будет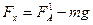 ,
,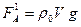 .
.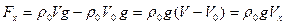 .
.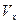 - объем шарового слоя высотой х, причем
- объем шарового слоя высотой х, причем 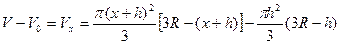 .
.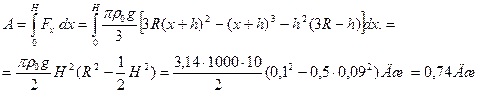
 .
.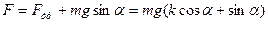
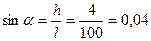 ;
; 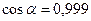 .
.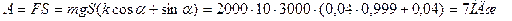
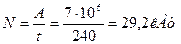
 ;
;  .
.