Примеры выполнения типовых заданий.
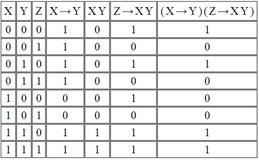
Пример 1. Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
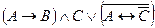
Решение.
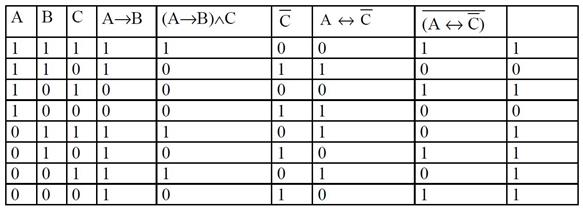
Данная формула является выполнимой и опровержимой.
Задания для совместного решения
Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
1. 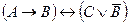
2. 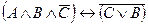
3. 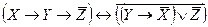
4. 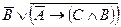
5. 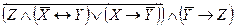
Ответы:
| 1 | 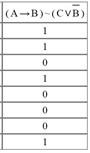
| 2 | 
| 3 | 
| 4 | 
| 5 | 
|
Индивидуальные контрольные задания.
Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
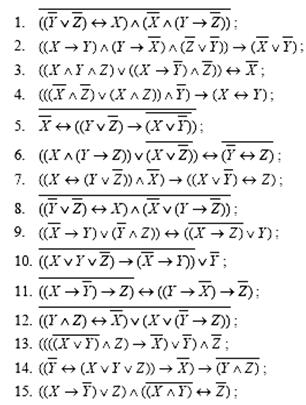
| 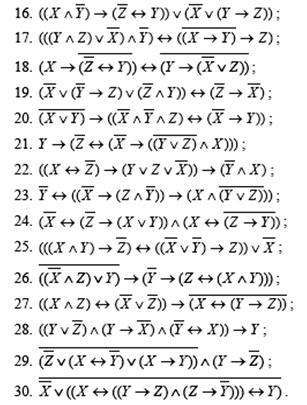
|
Практическая работа №2. Упрощение формул логики с помощью равносильных преобразований.
Краткие теоретические сведения.
Законы логики. Равносильные преобразования.
Две формулы F и G называются равносильными, если на любых равных наборах переменных значения формул равны.
Обозначение: 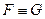
Для проверки равносильности можно использовать таблицу истинности или равносильные преобразования.
1. Коммутативность:
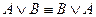 ,
,
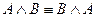 .
.
2. Ассоциативность:
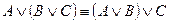 ,
,
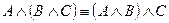 .
.
3. Дистрибутивность:
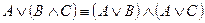 ,
,
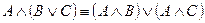 .
.
4. Идемпотентность:
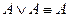 ,
,
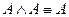 .
.
5. Закон двойного отрицания:
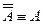 .
.
6. Закон исключения третьего:
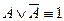 .
.
7. Закон противоречия:
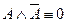 .
.
8. Законы де Моргана:
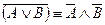 ,
,
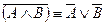 .
.
9. Свойства операций с логическими константами:
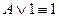 ,
,
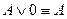 ,
,
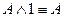 ,
,
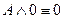 .
.
10. Склейки и поглощения
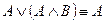
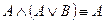
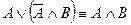
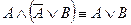
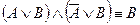
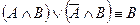
11. Выражение одних операций через другие
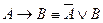
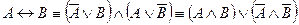
Примеры выполнения типовых заданий.
Пример №1.Упростить выражение и сделать проверку 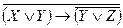
Решение.
1. Заменим импликацию на дизъюнкцию:
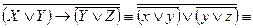
2. Снимем отрицания по закону Де Моргана.
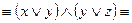
3. Вынесем за скобку общий множитель:
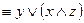 .
.
Выполним проверку
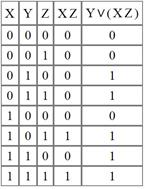
Значения формул совпали на всех наборах переменных.
Пример №2.
С помощью логических преобразований докажите тождественную истинность формулы:



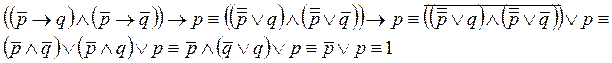
Вынесение за скобку закон А.Л.=1, a 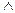 1= a
1= a
Пример 3
С помощью логических преобразований докажите тождественную ложность формулы

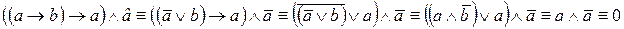 поглощение
поглощение
Задания для совместного решения
1. Упростить выражения:
а) 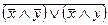 Ответ: х
Ответ: х
б) 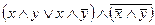 Ответ: х
Ответ: х
в) 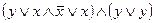 Ответ: у
Ответ: у
г) 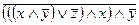 Ответ:
Ответ: 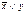
д) 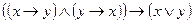 Ответ:
Ответ: 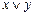
е) 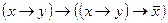 Ответ:
Ответ: 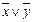
2. С помощью преобразований установить, какие из формул являются тождественно-истинными, а какие тождественно-ложными:
а) 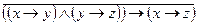
б) 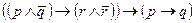
Ответ: а) ТЛ б) ТИ
Индивидуальные контрольные задания.
С помощью равносильных преобразований упростить формулу алгебры логики и выполнить проверку с помощью таблицы истинности.
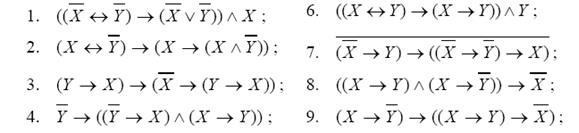
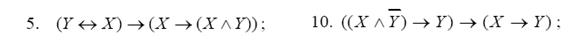

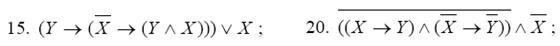
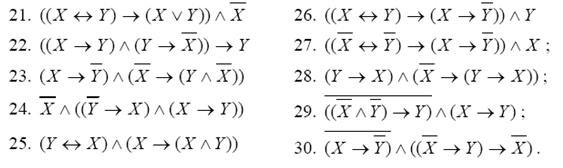
Тема 1.2. Булевы функции
Практическая работа №3. Приведение формул логики к ДНФ, КНФ с помощью равносильных преобразований
Примеры выполнения типовых заданий.
Пример №1. Данную формулу с помощью равносильных преобразований привести к ДНФ и КНФ. Считая, что формула задает булеву функцию, задать ее с помощью таблицы истинности, вектора значений, характеристических множеств и единичного куба.
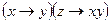
Решение.
Выразим все связки через  и
и  :
:
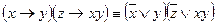
На основании закона дистрибутивности для получения ДНФ раскроем скобки так, чтобы все конъюнкции выполнялись вперед дизъюнкций:

Используем законы идемпотентности и противоречия:
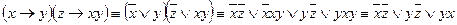 – ДНФ.
– ДНФ.
Для получения КНФ вернемся к первому шагу преобразований и применим закон дистрибутивности, но только во второй скобке:
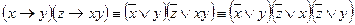 – КНФ.
– КНФ.
Составим таблицу истинности для формулы:
Тогда вектор значений функции будет иметь вид:
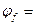 10100011
10100011
Характеристические множества:
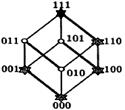
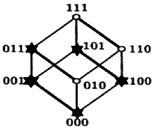
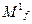 = {000,010,110,111},
= {000,010,110,111}, 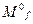 = {001,011,100,101}.
= {001,011,100,101}.
Единичный куб будет иметь вид:
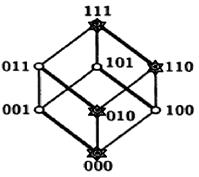
Задания для совместного решения.
С помощью равносильных преобразований привести данную формулу к ДНФ, КНФ. Считая, что формула задает булеву функцию, задать ее с помощью таблицы истинности, вектора значений, характеристических множеств и единичного куба.
1. 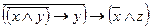
2. 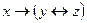
3. 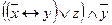
4. 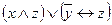
Ответы:
| ДНФ | КНФ | |
| 1 | 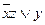
| 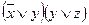
|
| 2 | 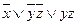
| 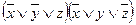
|
| 3 | 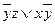
| 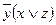
|
| 4 | 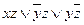
| 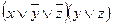
|
Индивидуальные контрольные задания.
С помощью равносильных преобразований привести данную формулу к ДНФ, КНФ. Считая, что формула задает булеву функцию, задать ее с помощью таблицы истинности, вектора значений, характеристических множеств и единичного куба.
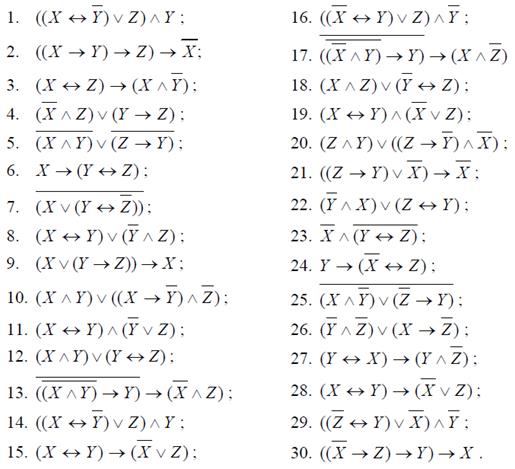
Практическая работа №4. Представление булевой функции в виде СДНФ и СКНФ.
Примеры выполнения типовых заданий.
Применяя равносильные преобразования, найти СДНФ и СКНФ для данной формулы. Проверить результат с помощью таблицы истинности.
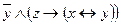
1. Получим ДНФ:
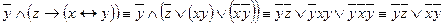 – ДНФ.
– ДНФ.
2. Добавим в каждый неполный конъюнкт переменную и ее отрицание, пока все конъюнкты не станут полными:
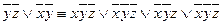
3. Уберем одинаковые члены все, кроме одного:
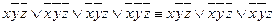 – СДНФ.
– СДНФ.
4. Получим КНФ:
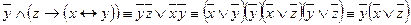 – КНФ
– КНФ
5. Получим СКНФ:
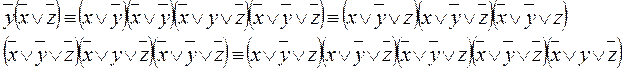
6. Для проверки построим таблицу истинности исходной формулы.
| x | y | z | 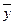
| 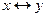
| 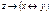
| f | СДНФ | СКНФ |
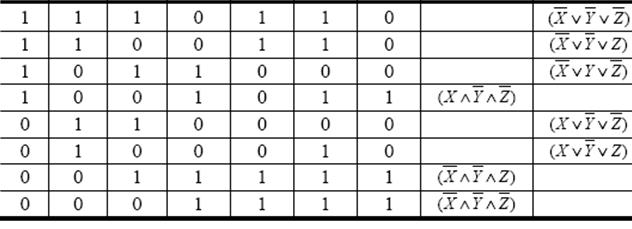
Задания для совместного решения.
Применяя равносильные преобразования, найти СДНФ и СКНФ для данной формулы. Проверить результат с помощью таблицы истинности.
1. 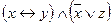
2. 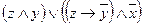
3. 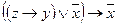
4. 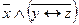
5. 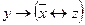
Ответ:
| СДНФ | СКНФ | |
| 1 | 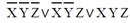
| 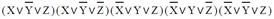
|
| 2 | 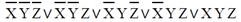
| 
|
| 3 | 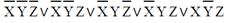
| 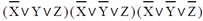
|
| 4 | 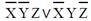
| 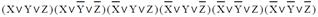
|
| 5 | 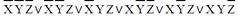
| 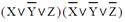
|
Индивидуальные контрольные задания.
Применяя равносильные преобразования, найти СДНФ и СКНФ для данной формулы. Проверить результат с помощью таблицы истинности.
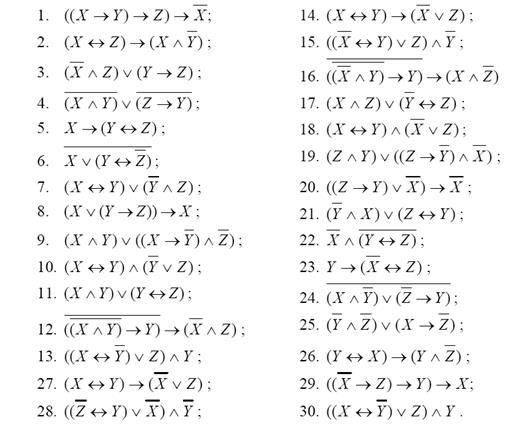
Практическая работа №5. Представление булевой функции в виде минимальной ДНФ
Примеры выполнения типовых заданий.
Пример №1. Найти МДНФ для функции, заданной СДНФ методом Квайна:
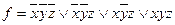 .
.
Решение.
1. 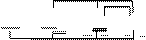 Произведем неполное склеивание. Первый конъюнкт склеивается со вторым, второй с третьим, третий с четвертым.
Произведем неполное склеивание. Первый конъюнкт склеивается со вторым, второй с третьим, третий с четвертым.
2. 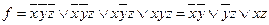 – сокращенная ДНФ.
– сокращенная ДНФ.
2. Строим матрицу Квайна:
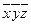
| 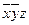
| 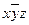
| 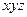
| |
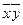
| * | * | ||
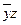
| * | * | ||
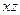
| * | * |
Ядро 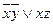 - содержит * во всех столбцах матрицы.
- содержит * во всех столбцах матрицы.
Ответ: МДНФ 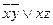 .
.
Пример №2. Найти МДНФ для функции, заданной СДНФ методом Квайна:
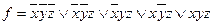 .
.
Решение.
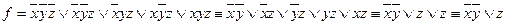 .
.
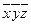
| 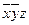
| 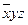
| 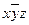
| 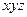
| |
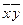
| * | * | |||
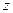
| * | * | * | * |
Ядро: 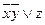 содержит * во всех столбцах матрицы.
содержит * во всех столбцах матрицы.
Ответ: МДНФ 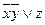 .
.
Пример №3. Найти МДНФ для функции, заданной СДНФ методом Квайна:
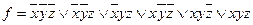 .
.
Решение.
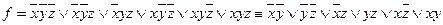 .
.
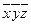
| 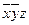
| 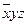
| 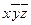
| 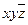
| 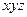
| |
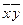
| * | * | ||||
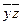
| * | * | ||||
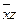
| * | * | ||||
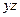
| * | * | ||||
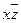
| * | * | ||||
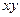
| * | * |
В каждом столбце стоит по 2 *, значит, у функции нет ядра. Тогда будем составлять все возможные пары, тройки, четверки и т.д. дизъюнкции простых импликант, проверяя покрытие столбиков *. Получим два ответа.
Ответ: МДНФ 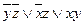
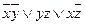
Пример №4. Найти МДНФ для функции геометрическим методом: (11010101)
Решение.
Изобразим единичный куб. Построим таблицу истинности:
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Получим куб:
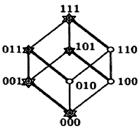
Ему соответствуют интервалы: 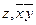 (грань и одно ребро).
(грань и одно ребро).
Тогда ядро: 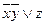 - является МДНФ, так как задействованы все вершины, помеченные *.
- является МДНФ, так как задействованы все вершины, помеченные *.
Ответ: МДНФ 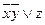 .
.
Пример №5. Найти МДНФ для функции геометрическим методом: (11001011)
Решение.
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
 Интервалы:
Интервалы: 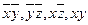
Ядро: 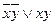
Ядро содержит не все вершины, отмеченные *, будем добавлять к нему по одному, по два и т.д. неядровые интервалы, пока не получим полное покрытие.
Ответ: МДНФ 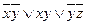 ,
, 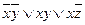
Пример №6. Найти МДНФ для функции методом Карно: (11010101)
Решение.
Исходная функция зависит от трех переменных, таблицу истинности
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
можно представить виде:
| yz x |  00 00
|  01 01
| 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
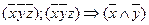
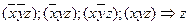
Ответ: МДНФ: 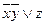 .
.
Пример №7. Найти МДНФ для функции методом Карно: (11001011)
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| yz x |   00 00
| 01 | 11 | 10 | 00 |
| 0 | 1 | 1 | 0 |  0 0
| 1 |
| 1 | 1 | 0 |  1 1
| 1 | 1 |
Интервалы: 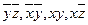
Ответ: МДНФ 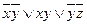 ,
, 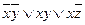
Задания для совместного решения.
Найти МДНФ для заданных функций методом Квайна, геометрическим методом и методом Карно.
| Ответы: | |||
| 1 | (10010110) | 1 | 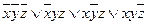
|
| 2 | (00110010) | 2 | 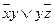
|
| 3 | (11001100) | 3 | 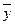
|
| 4 | (10101101) | 4 | 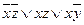
|
| 5 | (01010010) | 5 | 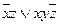
|
Индивидуальные контрольные задания.
Найти МДНФ для заданных функций методом Квайна, геометрическим методом и методом Карно.
| Вариант | f | Вариант | f | Вариант | f |
| 1 | 00011001 | 11 | 01010101 | 21 | 00110001 |
| 2 | 01100100 | 12 | 10101010 | 22 | 10000001 |
| 3 | 01000100 | 13 | 00100111 | 23 | 01111110 |
| 4 | 01101110 | 14 | 11100011 | 24 | 10001110 |
| 5 | 01110001 | 15 | 00000110 | 25 | 01110001 |
| 6 | 11111100 | 16 | 10101100 | 26 | 00001110 |
| 7 | 00011011 | 17 | 00010001 | 27 | 10010010 |
| 8 | 11011111 | 18 | 00100110 | 28 | 00110100 |
| 9 | 00100010 | 19 | 11001111 | 29 | 11000001 |
| 10 | 01001010 | 20 | 10010011 | 30 | 11111011 |
Практическая работа №6. Построение и оптимизация РКС
Примеры выполнения типовых заданий.
Пример № 1. Построить наиболее простую релейно-контактную схему по заданной функции проводимости (11011100)
Решение.
- Строим таблицу истинности.
| x | y | z | f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
- Находим МДНФ, например геометрическим методом.
 Интервалы:
Интервалы: 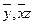
Ядро: 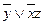
МДНФ: 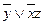
- Упростить формулу невозможно (отсутствуют общие множители).
- Реализуем схему:
|
| ||||||
|
|
| |||||
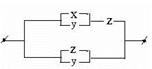
Пример № 2. Упростить следующую РКС. Сделать проверку с помощью функции проводимости:
Решение.
Запишем РКС в виде формулы алгебры логики:
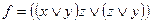 .
.
Упростим эту формулу:
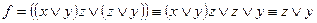
Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:
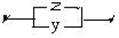
Функция проводимости для схем задается следующей таблицей:
| x | y | z | f1(x,y,z) | f2(x,y,z) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
Как видно из таблицы, функции проводимости совпадают.
Задания для совместного решения.
1.Построить РКС с данной функцией проводимости:
| Ответы | |||
| 1 | 00110010 | 1 | 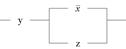
|
| 2 | 11011110 | 2 | 
|
| 3 | 00110000 | 3 | 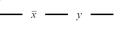
|
2. Упростить РКС и выполнить проверку с помощью функции проводимости:
| Ответы | |||
| 1 | 
| 1 | 
|
| 2 | 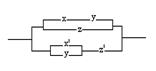
| 2 | 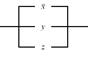
|
| 3 | 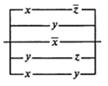
| 3 | 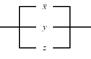
|
| 4 | 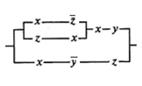
| 4 | 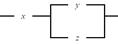
|
| 5 | 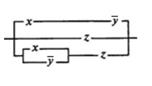
| 5 | 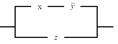
|
Индивидуальные контрольные задания.
1. Построить РКС с минимальным количеством элементов с данной функцией проводимости.
2. Упростить РКС и выполнить проверку с помощью функции проводимости
| Вариант | №1 | №2 | Вариант | №1 | №2 |
| 1 | 11111011 | 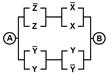
| 16 | 01000100 | 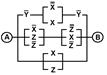
|
| 2 | 00110100 | 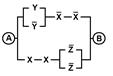
| 17 | 10010010 | 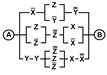
|
| 3 | 00001110 | 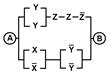
| 18 | 11000001 | 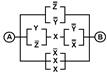
|
| 4 | 10001110 | 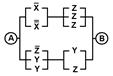
| 19 | 01110001 | 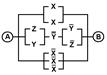
|
| 5 | 10000001 | 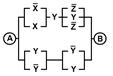
| 20 | 01111110 | 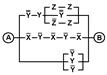
|
| 6 | 00110001 | 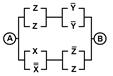
| 21 | 11001111 | 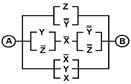
|
| 7 | 10010011 | 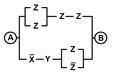
| 22 | 00100110 | 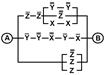
|
| 8 | 00010001 | 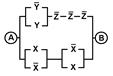
| 23 | 10101100 | 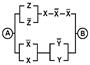
|
| 9 | 00000110 | 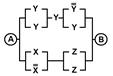
| 24 | 11100011 | 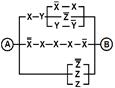
|
| 10 | 00100111 | 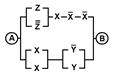
| 25 | 10101010 | 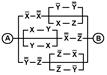
|
| 11 | 01010101 | 
| 26 | 00100010 | 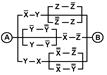
|
| 12 | 01001010 | 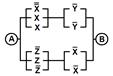
| 27 | 00011011 | 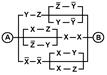
|
| 13 | 11011111 | 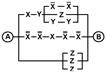
| 28 | 01101110 | 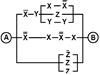
|
| 14 | 11111100 | 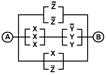
| 29 | 11010101 | 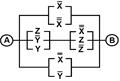
|
| 15 | 01110001 | 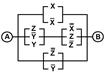
| 30 | 01100100 | 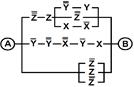
|
Практическая работа №7. Построение многочлена Жегалкина
Примеры выполнения типовых заданий.
Пример №1. Найти многочлен Жегалкина для функции, заданной формулой. Результат проверить с помощью таблицы истинности:
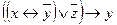
Решение.
Преобразуем данное выражение:
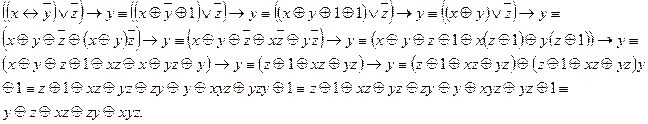 Построим таблицу истинности:
Построим таблицу истинности:
| x | y | z | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
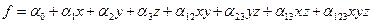
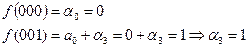
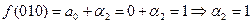
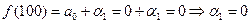
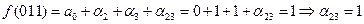
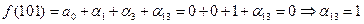
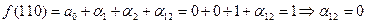
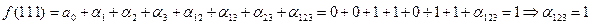
Тогда многочлен Жегалкина имеет вид:
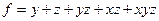 .
.
Результаты совпали.
Ответ: 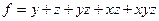
Задания для совместного решения.
С помощью равносильных преобразований привести данную формулу алгебры логики к виду многочлена Жегалкина. Результат проверить с помощью таблицы истинности.
| Ответы | |||
| 1 | 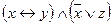
| 1 | 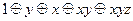
|
| 2 | 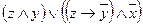
| 2 | 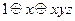
|
| 3 | 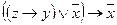
| 3 | 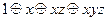
|
| 4 | 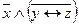
| 4 | 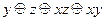
|
| 5 | 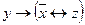
| 5 | 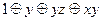
|
Индивидуальные контрольные задания.
С помощью равносильных преобразований привести данную формулу алгебры логики к виду многочлена Жегалкина. Результат проверить с помощью таблицы истинности.
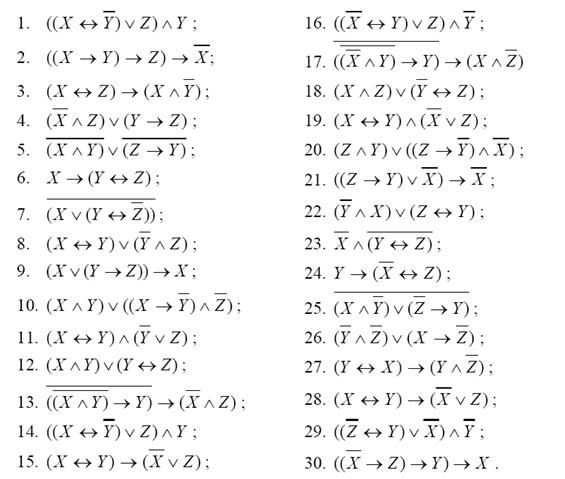
Практическая работа №8. Проверка булевой функции на принадлежность к классам Т0, Т1, S, L, M. Полнота множеств.
Примеры выполнения типовых заданий.
Пример №1. Выяснить, каким классам Поста принадлежит функция 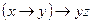 .
.
Решение.
Строим таблицу истинности.
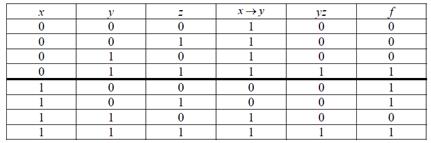
С помощью таблицы выясняем, что 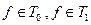 .
.
Для проверки на самодвойственность сделаем поворот и инверсию последнего столбика:
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
Первый и последний столбик не совпали, значит 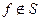 .
.
Проверяем на монотонность. Для этого сравниваем с первым набором все нижестоящие и для тех, что 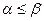 , проверяем, что
, проверяем, что 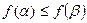 . Затем сравниваем наборы, стоящие под вторым, потом под третьим и так далее по всей таблице. Это условие не выполнено для пятого и седьмого набора:
. Затем сравниваем наборы, стоящие под вторым, потом под третьим и так далее по всей таблице. Это условие не выполнено для пятого и седьмого набора: 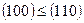 ,
, 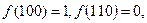
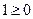 . Значит
. Значит 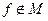 .
.
Для проверки на линейность найдем многочлен Жегалкина.
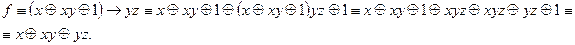
Значит 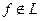 .
.
Ответ: 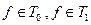 ,
, 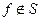 ,
, 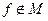 ,
, 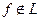 .
.
Пример №2. Проверить множество булевых функций на полноту:
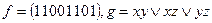 .
.
Заполним таблицу Поста.
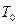
| 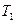
| S | L | M | |
| f | – | + | – | – | – |
| g | + | + | + | – | + |
Для первой функции составим многочлен Жегалкина методом неопределенных коэффициентов. Остальные классы проверяются по таблице истинности.
| x | y | z | f | f * | |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
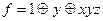 .
.
Для второй функции сначала заполним таблицу истинности:
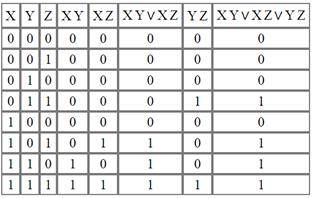 .
.
По ней определяем принадлежность классам. Многочлен Жегалкина будет иметь вид: 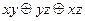 .
.
Система функций не является полной, так как обе функции принадлежат классу 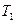 .
.
Ответ: не полная.
Задания для совместного решения.
1. Выяснить, каким классам Поста принадлежит функция:
| Ответ | |||||||
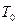
| 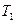
| S | L | M | |||
| а | 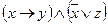
| а | – | + | – | – | – |
| б | 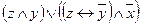
| б | + | + | + | – | – |
| в | 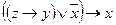
| в | + | + | + | + | + |
| г | 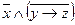
| г | + | – | – | – | – |
| д | 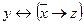
| д | – | + | – | – | – |
2. Выясните, является ли система булевых функций 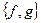 полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
| f | g | Ответ | ||
| а | 00110011 | 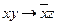
| а | полная |
| б | 10110101 | 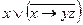
| б | не полная |
| в | 11001010 | 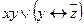
| в | полная |
Индивидуальные контрольные задания.
1. Выяснить, каким классам Поста принадлежит функция.
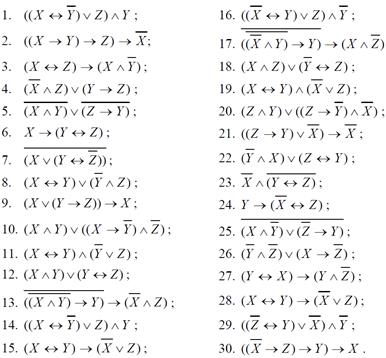
2. Выясните, является ли система булевых функций 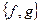 полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
полной по теореме Поста. Функция f задана вектором значений, функция g задана формулой.
| f | g | f | g | ||
| 1 | 10101100 | 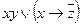
| 16 | 01000100 | 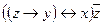
|
| 2 | 00000110 | 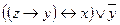
| 17 | 11111011 | 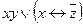
|
| 3 | 11100011 | 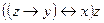
| 18 | 11000001 | 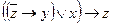
|
| 4 | 00100111 | 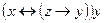
| 19 | 00110100 | 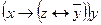
|
| 5 | 10101010 | 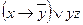
| 20 | 10010010 | 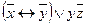
|
| 6 | 01010101 | 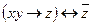
| 21 | 00001110 | 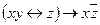
|
| 7 | 01001010 | 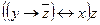
| 22 | 01110001 | 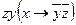
|
| 8 | 00100010 | 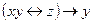
| 23 | 10001110 | 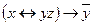
|
| 9 | 11011111 | 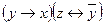
| 24 | 01111110 | 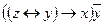
|
| 10 | 00011011 | 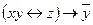
| 25 | 10000001 | 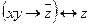
|
| 11 | 11111100 | 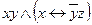
| 26 | 00110001 | 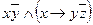
|
| 12 | 01110001 | 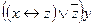
| 27 | 11001111 | 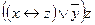
|
| 13 | 01101110 | 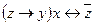
| 28 | 10010011 | 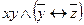
|
| 14 | 11010101 | 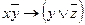
| 29 | 00100110 | 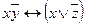
|
| 15 | 01100100 | 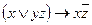
| 30 | 00010001 | 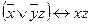
|
Практическая работа №9. Контрольная работа №1
Индивидуальные контрольные задания.
1. Функция задана формулой. Найти:
а) таблицу истинности;
б) ДНФ и КНФ;
в) СДНФ и СКНФ;
г) МДНФ;
д) РКС с минимальным числом элементов, имеющих функцию проводимости, аналогичную данной функции;
е) Каким классам Поста принадлежит данная функция?
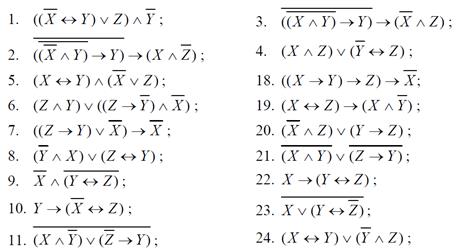
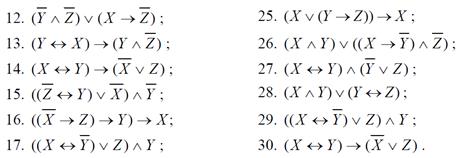
Раздел 2. Элементы теории множеств
Тема 2.1. Основы теории множеств
Практическая работа №10. Множества и основные операции над ними. Графическое изображение множеств на диаграммах Эйлера-Венна.
Примеры выполнения типовых заданий.
Пример №1. Проверить равенство двух множеств тремя способами:
а) по определению
б) диаграммами Эйлера-Венна
в) с помощью формул алгебры логики
A \ (B È C) = (A \ B) Ç (A \ C).
Решение.
а) По определению следует, что если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.
Множество A \ B представляет собой множество элементов множества А, не принадлежащих множеству В.
Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.
Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.
Таким образом, тождество можно считать доказанным.
б) На рисунке 9 показано изображение искомого множества левой и правой части равенства: штриховкой показаны промежуточные результаты, результат залит заливкой.
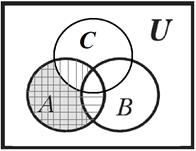
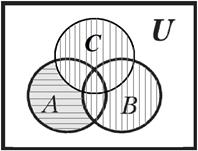
Рисунок 9 – Построение диаграммы Эйлера-Вена
в) Используя соответствие теоретико-множественных операций логическим операциям, упростим левую и правую часть равенства:
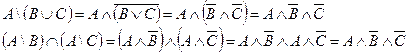
Результаты совпали, значит формула верна.
Пример №2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 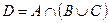 ,
, 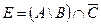 .
.
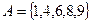 ,
, 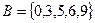 ,
, 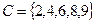 .
.
Решение.
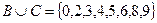 ,
, 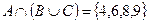 .
.
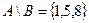 ,
, 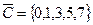 ,
, 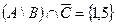
Задания для совместного решения.
1. Проверить равенство двух множеств тремя способами:
- по определению
- диаграммами Эйлера-Венна
- с помощью формул алгебры логики
б. A 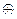 B = (A È B) \ (A Ç B);
B = (A È B) \ (A Ç B);
в. A \ (A \ B) = A Ç B;
г. A Ç (B 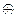 C) = (A Ç B)
C) = (A Ç B) 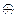 (A Ç C);
(A Ç C);
д. (A \ B) \ C = A \ (B È C).
2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 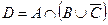 ,
, 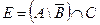 .
.
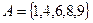 ,
, 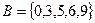 ,
, 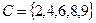 .
.
Индивидуальные контрольные задания.
1. Проверить равенство двух множеств тремя способами:
- по определению
- диаграммами Эйлера-Венна
- с помощью формул алгебры логики
| 1 | 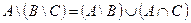
| 16 | 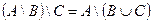
|
| 2 | 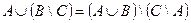
| 17 | 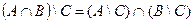
|
| 3 | 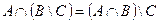
| 18 | 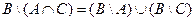
|
| 4 | 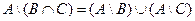
| 19 | 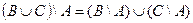
|
| 5 | 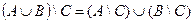
| 20 | 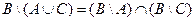
|
| 6 | 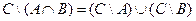
| 21 | 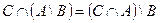
|
| 7 | 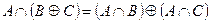
| 22 | 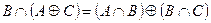
|
| 8 | 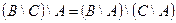
| 23 | 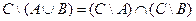
|
| 9 | 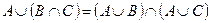
| 24 | 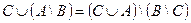
|
| 10 | 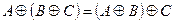
| 25 | 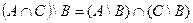
|
| 11 | 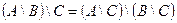
| 26 | 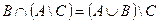
|
| 12 | 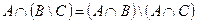
| 27 | 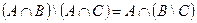
|
| 13 | 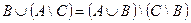
| 28 | 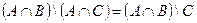
|
| 14 | 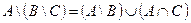
| 29 | 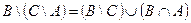
|
| 15 | 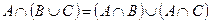
| 30 | 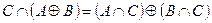
|
2. Заданы подмножества A, B и C множества арабских цифр. Найдите подмножества 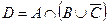 ,
, 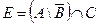 .
.
| 1. | A={1; 2; 3}, | B={1; 5; 6; 7}, | C={0; 4; 8; 9}. |
| 2. | A={0; 2; 7}, | B={1; 3; 5; 7}, | C={0; 2; 3; 8}. |
| 3. | A={1; 2; 7}, | B={1; 3; 5; 7}, | C={0; 2; 3; 7}. |
| 4. | A={1; 5; 8}, | B={1; 3; 5; 9}, | C={0; 2; 3; 7}. |
| 5. | A={1; 5; 8}, | B={1; 3; 6; 7}, | C={0; 3; 4; 8}. |
| 6. | A={1; 2; 3; 5}, | B={1; 3; 5; 7}, | C={1; 2; 5; 8}. |
| 7. | A={1; 2; 3; 5}, | B={1; 3; 5}, | C={1; 2; 5; 8}. |
| 8. | A={1; 2; 3; 5}, | B={1; 3; 7}, | C={1; 2; 5; 9}. |
| 9. | A={1; 2; 3; 5}, | B={3; 5; 7}, | C={1; 2; 5; 6}. |
| 10. | A={1; 2; 3; 5}, | B={1; 5; 8}, | C={1; 3; 5; 8}. |
| 11. | A={1; 2; 3; 5; 9}, | B={1; 3; 5; 7}, | C={5; 8}. |
| 12. | A={1; 2; 3; 5; 8}, | B={1; 3; 5; 8}, | C={5; 8}. |
| 13. | A={1; 2; 3; 5; 9}, | B={1; 3; 5; 7}, | C={5; 9}. |
| 14. | A={1; 2; 3; 7; 9}, | B={1; 3; 5; 7}, | C={8; 9}. |
| 15. | A={0; 2; 3; 5; 9}, | B={1; 2; 6; 7}, | C={7; 9}. |
| 16. | A={0; 2; 3; 5; 9}, | B={1; 2; 7}, | C={2; 3; 6; 7; 9}. |
| 17. | A={0; 2; 4; 5; 9}, | B={1; 2; 6}, | C={2; 3; 4; 7; 8}. |
| 18. | A={0; 2; 3; 5; 9}, | B={1; 2; 7}, | C={0; 3; 5; 6; 9}. |
| 19. | A={0; 2; 3; 5; 9}, | B={1; 2; 8}, | C={0; 3; 5; 6; 8}. |
| 20. | A={0; 2; 3; 4; 6}, | B={1; 2; 7}, | C={0; 4; 5; 6; 7}. |
| 21. | A={0; 2}, | B={1; 2; 7}, | C={0; 3; 5}. |
| 22. | A={0; 2}, | B={1; 2; 5}, | C={0; 4; 5}. |
| 23. | A={1; 2}, | B={1; 2; 3}, | C={0; 3; 5}. |
| 24. | A={1; 2}, | B={0; 2; 4}, | C={0; 3; 4}. |
| 25. | A={0; 3}, | B={1; 2; 3}, | C={0; 3; 5}. |
| 26. | A={0; 2; 3; 5; 9}, | B={1; 2; 7; 8; 9}, | C={0; 3; 5; 6; 9}. |
| 27. | A={1; 2; 4; 5; 7}, | B={1; 2; 7; 8; 9}, | C={0; 3; 5; 6; 9}. |
| 28. | A={1; 2; 4; 5; 7}, | B={1; 3; 6; 8; 9}, | C={0; 3; 5; 6; 8}. |
| 29. | A={1; 3; 4; 5; 7}, | B={1; 3; 6; 8}, | C={2; 3; 5; 6; 7}. |
| 30. | A={0; 3; 4; 6; 7}, | B={1; 3; 6; 7; 9}, | C={0; 2; 5; 6; 8}. |
Практическая работа №11. Исследование свойств бинарных отношений.
Примеры выполнения типовых заданий.
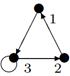
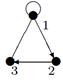
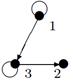
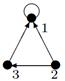
Пример №1. На множестве М {1, 2, 3, 4 } задано бинарное отношение 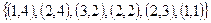 . Составить матрицу отношения, граф отношения. Определить вид отношения.
. Составить матрицу отношения, граф отношения. Определить вид отношения.
Решение.
Матрица отношения будет иметь вид:
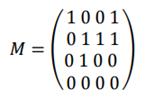 .
.
Граф отношения будет иметь вид:
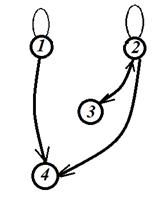
Отношение не относится ни к одному из указанных выше видов.
Пример №2. Пусть A={1, 2, 3, 4}, на множестве A заданы два отношения:
R={(x, y) | 2x 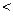 y} и P={(x, y) | x+3y делится на 2}. Какими свойствами обладают отношения R, P?
y} и P={(x, y) | x+3y делится на 2}. Какими свойствами обладают отношения R, P?
Решение.
Запишем отношения в виде множеств:
R={(1,2); (1,3); (1,4); (2,4)}. В частности, 1R2, поскольку 2·1 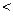 2.
2.
P={(1,1); (1,3); (2,2); (2,4); (3,1); (3,3); (4,2); (4,4)}. В частности, 1P3, поскольку 1+3·3 делится на 2.
Запишем матрицы отношений:
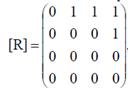 ,
, 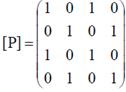 .
.
Отношение P является рефлексивным, а отношение R не является рефлексивным (в матрицах отношений на главной диагонали имеются нули).
Отношение R является антирефлексивным, а отношения P не является антирефлексивным (в матрицах отношений на главной диагонали имеются единицы).
Найдем транспонированные матрицы отношений.
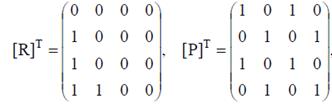 .
.
Из сравнения матриц отношений с транспонированными матрицами этих отношений, находим, что отношение P является симметричным, а отношения R не является симметричным. Отношение R является антисимметричными (у матрицы [R] и [R]T нет совпадающих единиц вне главной диагонали), а отношение P не является антисимметричным (например, p13=p31=1).
Для определения транзитивности отношений найдем произведения каждой матрицы на саму себя.

Задания для совместного решения.
На множестве М {1, 2, 3, 4} задано бинарное отношение
1. 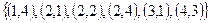 .
.
2. 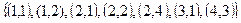
3. 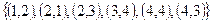
4. 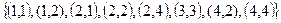
Составить матрицу отношения, граф отношения. Определить вид отношения.
Индивидуальные контрольные задания.
На множестве М {1, 2, 3, 4} задано бинарное отношение наборами пар. Составить матрицу отношения, граф отношения. Определить вид отношения.
| 1 | R={(1;1); (1;2); (1;3); (1;4); (2;2); (2;3); (2;4); (3;3); (3;4); (4;4)}. | 16 | R={(1;1); (1;2); (1;4); (2;2); (2;4); (3;3); (3;4); (4;4)}. |
| 2 | R={(1;1); (2;1); (1;2); (2;4); (4;2); (1;4); (4;1)}. | 17 | R={(1;1); (1;2); (2;4); (4;2); (1;4); (4;1); (4;3)}. |
| 3 | R={(2;1); (1;2); (2;3); (3;2); (1;3); (3;1)}. | 18 | R={(2;1); (1;2); (2;3); (3;2); (1;3); (3;1); (4;3)}. |
| 4 | R={(1;2); (2;3); (3;4); (4;1)}. | 19 | R={(1;2); (2;3); (3;4); (4;1);(4;3)}. |
| 5 | R={(1;1); (2;1); (2;2); (3;1); (3;2); (3;3); (4;1); (4;2); (4;3)}. | 20 | R={(1;1); (2;1); (2;2); (3;1); (3;2); (3;3); (4;1); (4;3)}. |
| 6 | R={(2;1); (2;2); (2;4); (3;4); (4;1); (4;2); (4;3); (4;4)} | 21 | R={(2;1); (2;2); (2;4); (3;3); (4;1); (4;2); (4;3); (4;4)} |
| 7 | R={(1;3); (2;4); (3;1); (3;4); (4;2); (4;3)}. | 22 | R={(1;3); (2;4); (3;1); (3;4); (4;2); (4;3);(4;4)}. |
| 8 | R={(1;1); (2;1); (2;3); (2;4); (3;2); (3;3); (3;4); (4;3); (4;4)}. | 23 | R={(1;1); (2;1); (2;2); (2;4); (3;2); (3;3); (3;4); (4;3); (4;4)}. |
| 9 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (3;3); (4;1); (4;4)}. | 24 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (4;1); (4;4)}. |
| 10 | R={(1;3); (2;1); (2;2); (2;4); (3;2); (3;4); (4;4)}. | 25 | R={(1;3); (2;1); (2;2); (2;4); (3;2); (3;4);(4;3); (4;4)}. |
| 11 | R={(1;3); (1;4); (2;2); (2;3); (2;4); (4;2); (3;4); (4;4)}. | 26 | R={(1;1); (1;4); (2;2); (2;3); (2;4); (4;2); (3;3); (4;4)}. |
| 12 | R={(1;1); (1;2); (2;4); (2;2); (1;4); (3;3); (4;4)}. | 27 | R={(1;1); (2;2); (2;4); (2;2); (1;4); (3;3); (4;4)}. |
| 13 | R={(1;1); (2;1); (2;2); (4;2); (4;1); (4;4)}. | 28 | R={(1;1); (2;1); (2;2); (4;2); (4;1); (4;4);(4;3)}. |
| 14 | R={(1;1); (2;1); (1;2); (2;4); (2;2); (4;2); (1;4); (4;1); (4;4)}. | 29 | R={(1;1); (2;1); (1;2); (2;4); (2;3); (3;2); (1;4); (4;1); (4;4)}. |
| 15 | R={(1;2); (1;3); (1;4); (2;3); (2;4); (3;4)}. | 30 | R={(1;2); (1;3); (1;4); (3;3); (3;4); (4;4)}. |
Практическая работа №12. Теория отображений и алгебра подстановок.
Примеры выполнения типовых заданий.
Пример №1. Определить число инверсий и четность подстановки.
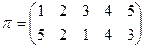 .
.
Решение.
С элементом 5 инверсию образуют все идущие за ним элементы 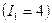 , с 2 инверсию образует только 1
, с 2 инверсию образует только 1 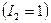 , с единицей нет инверсий, с 4 инверсию образует 3.
, с единицей нет инверсий, с 4 инверсию образует 3.
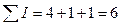 , четная подстановка.
, четная подстановка.
Пример №2. С данными подстановками выполните следующие операции:
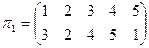 ,
, 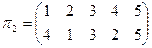 .
.
| а) | 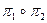
| б) | 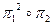
| в) | 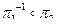
|
Решение.
а) 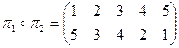 .
.
б) 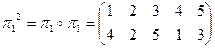 .
.
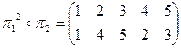 .
.
в) 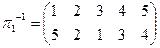 .
.
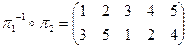 .
.
Пример №3. Даны подстановки:
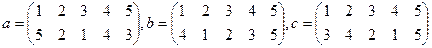 .
.
Решить уравнения: 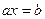 ,
, 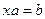 ,
, 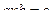 .
.
1. 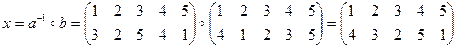 .
.
 2.
2. 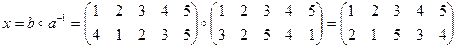
3.
Задания для совместного решения.
1. Определить число инверсий и четность подстановки:
а) 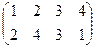 б)
б) 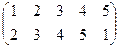 в)
в) 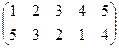
2. С данными подстановками выполните следующие операции:
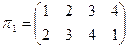
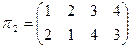
а) 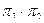 б)
б) 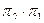 в)
в) 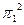
г) 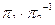 д)
д) 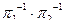 е)
е) 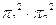
3. Решить уравнения:
а ) a × x = b б ) x × a = b в ) a × x × b = c
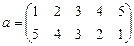
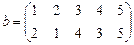
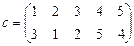 .
.
Ответы:
1. а) 3, нечетная б) 4, четная, в) 6, четная.
2. а) 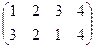 , б)
, б) 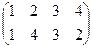 , в)
, в) 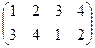 , г)
, г) 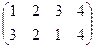
д) 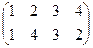 , е)
, е) 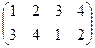 .
.
3. а) 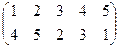 , б)
, б) 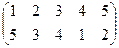 , в)
, в) 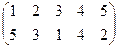 .
.
Индивидуальные контрольные задания.
1. Определить число инверсий и четность подстановок a, b, c.
2. С данными подстановками выполните следующие операции: 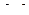 ,
, 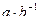 ,
, 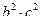 .
.
3. Решить уравнения:
а) a × x = b б) x × a = b в) a × x × b = c
| a | b | c | |
| 1 | 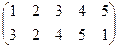
| 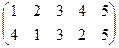
| 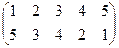
|
| 2 | 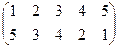
| 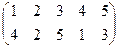
| 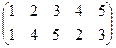
|
| 3 | 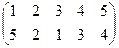
| 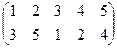
| 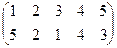
|
| 4 | 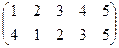
| 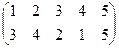
| 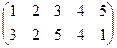
|
| 5 | 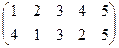
| 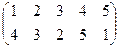
| 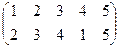
|
| 6 | 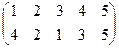
| 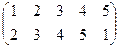
| 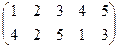
|
| 7 | 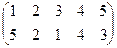
| 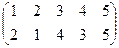
| 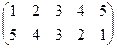
|
| 8 | 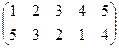
| 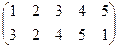
| 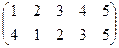
|
| 9 | 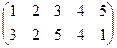
| 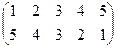
| 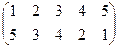
|
| 10 | 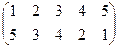
| 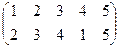
| 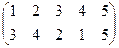
|
| 11 | 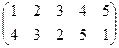
| 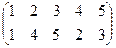
| 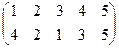
|
| 12 | 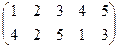
| 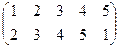
| 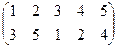
|
| 13 | 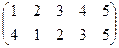
| 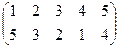
| 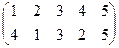
|
| 14 | 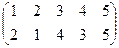
| 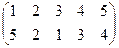
| 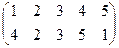
|
| 15 | 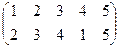
| 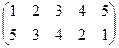
| 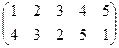
|
| 16 | 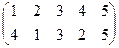
| 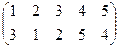
| 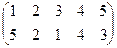
|
| 17 | 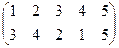
| 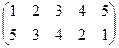
| 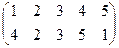
|
| 18 | 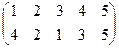
| 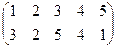
| 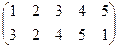
|
| 19 | 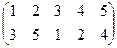
| 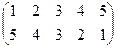
| 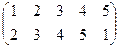
|
| 20 | 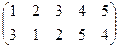
| 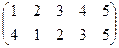
| 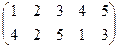
|
| 21 | 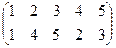
| 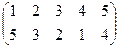
| 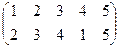
|
| 22 | 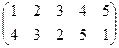
| 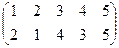
| 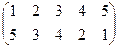
|
| 23 | 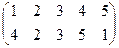
| 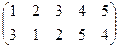
| 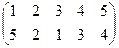
|
| 24 | 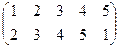
| 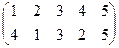
| 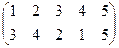
|
| 25 | 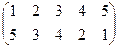
| 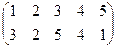
| 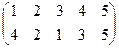
|
| 26 | 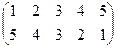
| 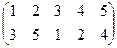
| 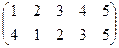
|
| 27 | 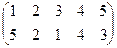
| 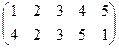
| 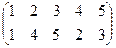
|
| 28 | 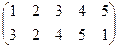
| 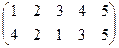
| 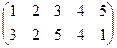
|
| 29 | 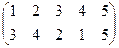
| 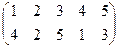
| 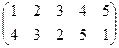
|
| 30 | 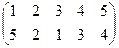
| 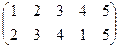
| 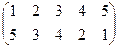
|
Раздел 3. Логика предикатов
Тема 3.1. Предикаты
Практическая работа №13. Нахождение области определения и истинности предиката. Построение отрицаний к предикатам, содержащим кванторные операции.
Примеры выполнения типовых заданий.
Пример №1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
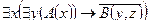 .
.
Решение.
Данное выражение является формулой, так как выполнены все условия 1-5 определения формулы в алгебре предикатов.
Свободные переменные : y, z.
Связанные переменные: x.
Пример №2. Даны предикаты: А(x) и B(x): А(x) = "x – деятельность"; B(x) = "x дает счастье". Записать словами предложенные формулы С и D:
C = "x(B(x) → A(x))
D = 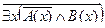
Решение.
C = "x(B(x) →A(x)) – Счастье дается от деятельности
D = 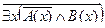
Преобразуем формулу: 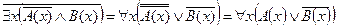
Безделье не приносит счастье.
Пример №3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Некоторые студенты сдали все зачеты.
Решение.
Пусть A(x)=”x – студенты”, B(y)=“y – сдать все зачеты”, C(x, y)=“x – сдать все зачеты y”
тогда
$x"y(A(x) 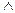 B(y) → C(x, y)) – Некоторые студенты сдали все зачеты.
B(y) → C(x, y)) – Некоторые студенты сдали все зачеты.
Строим отрицание:
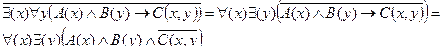
Это предложение можно прочитать следующим образом:
“Каждый студент не сдал хотя бы один зачет”.
Задания для совместного решения.
1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
"x,yA(x, y).
2. Даны предикаты А(x) и B(x): А(x) = "x – наука"; B(x) = "x гуманитарная". Записать словами предложенные формулы: 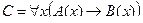 ,
, 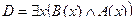 .
.
3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
Не все металлы твердые.
Индивидуальные контрольные задания.
1. Установить, является ли данное выражение формулой, а если да, то определить, какие переменные в ней свободные, а какие связанные.
2. Даны предикаты: А(x) и B(x). Записать словами предложенные формулы С и D.
3. Данное суждение записать в виде формулы логики предикатов. Построить отрицание данного суждения в виде формулы, не содержащей внешних знаков отрицания. Перевести на естественный язык.
| Задание 1 | Задание 2 | Задание 3 | |
| 1 | 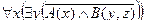
| А(x) = "x – торговец подержанными автомобилями";
B(x) = "x – нечестный человек".
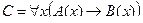
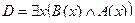
| Не всякое действительное число является рациональным |
| 2 | 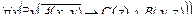
| А(x) = "x – торговец наркотиками";
B(x) = "x – наркоман".
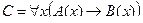
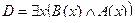
| Каждый студент выполнил хотя бы одну лабораторную работу |
| 3 | 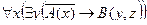
| А(x) = "x – рациональное число";
B(x) = "x – действительное число".
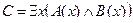
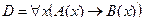
| Ни одно четное число, большее 2, не является простым. |
| 4 | 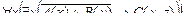
| А(x) = "x – политик";
B(x) = "x – мошенник".
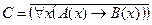
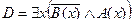
| Выгул собак или кошек запрещен. |
| 5 | 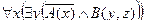
| А(x) = "x – рыба";
B(x) = "x – водное животное".
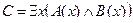
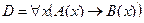
| Произведение любых двух простых чисел не является простым числом. |
| 6 | 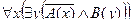
| А(x) = "x – четное число";
B(x) = "x делится на 6".
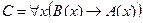
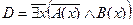
| Всякое положительное число больше всякого отрицательного числа. |
| 7 | 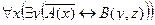
| А(x) = "x – металл";
B(x) = "x – теплопроводен".
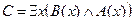
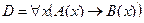
| Каждый, купивший билет, получит премию. |
| 8 | 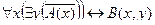
| А(x) = "x – простое число";
B(x) = "x четное число".
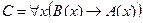
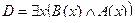
| Всякое положительное число больше всякого отрицательного числа. |
| 9 | 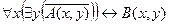
| А(x) = "x – студент";
B(x) = "x – сдал экзамены".
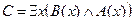
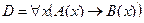
| Всякий равносторонний треугольник является равнобедренным. |
| 10 | 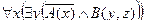
| А(x) = "x - деятельность";
B(x) = "x дает счастье".
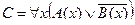
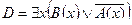
| Все студенты сдали все зачеты. |
| 11 | 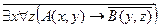
| А(x) = "x – ученый";
B(x) = "x – мыслит формулами".
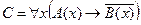
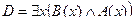
| Все депутаты голосовали за этот законопроект. |
| 12 | 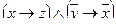
| А(x) = "x – планета";
B(x) = "x светит собственным светом".
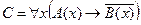
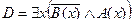
| Все рыбы живут в воде. |
| 13 | 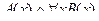
| А(x) = "x – педагог";
B(x) = "x – учитель".
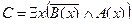
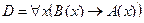
| Некоторые абитуриенты поступили в институт. |
| 14 | 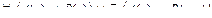
| А(x) = "x – морское животное"; B(x) = "x дышит жабрами".
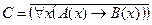
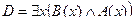
| Студент ответил на некоторые вопросы. |
| 15 | 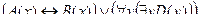
| А(x) = "x – гриб";
B(x) = "x съедобен".
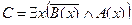
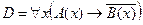
| Автобус останавливается на всех остановках. |
| 16 | 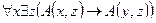
| А(x) = "x – существительное"; B(x) = "x обозначает предмет".
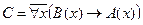
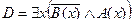
| Некоторые зрители не любят некоторых артистов |
| 17 | 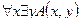
| А(x) = "x – суждение";
B(x) = "x выражается предложением".
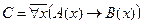
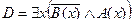
| В этой местности иногда бывает снег. |
| 18 | 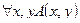
| А(x) = "x – наука";
B(x) = "x гуманитарная".
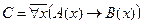
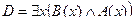
| Не все металлы твердые. |
| 19 | 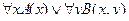
| А(x) = "x – газ";
B(x) = "x бесцветный".
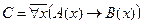
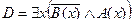
| Некоторые студенты получают стипендию. |
| 20 | 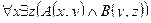
| А(x) = "x – пассажир";
B(x) = "x платит за проезд".
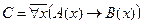
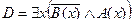
| Некоторые книги полезны. |
| 21 | 
| А(x) = "x – товар";
B(x) = "x ввозится контрабандным путем".
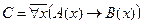
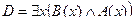
| Существуют непрерывные функции, которые не являются дифференцируемыми. |
| 22 | 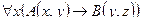
| А(x) = "x – пошлина";
B(x) = "x взимается с цены товара".
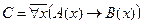
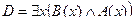
| Он ничего не знает. |
| 23 | 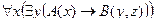
| А(x) = "x – человек";
B(x) = "x знает, кто такой Альфред Брем".
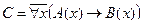
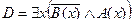
| Некоторые пассажиры не платят за проезд. |
| 24 | 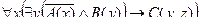
| А(x) = "x насекомое";
B(x) = "x беспозвоночное".
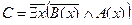
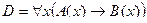
| Не все полезное приятно. |
| 25 | 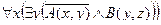
| А(x) = "x – рыба";
B(x) = "x дышит жабрами".
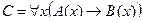
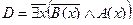
| Не всякий газ бесцветен. |
| 26 | 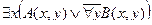
| А(x) = "x – алгоритм";
B(x) = "x сходится".
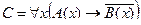
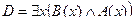
| Все люди хорошие. |
| 27 | 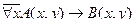
| А(x) = "x – издательство";
B(x) = "x выпускает учебники".
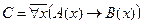
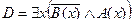
| Некоторые студенты досрочно сдали экзамены. |
| 28 | 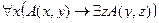
| А(x) = "x – целое число";
B(x) = "x – рациональное число ".
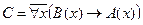
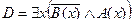
| Не все государства подписали это соглашение. |
| 29 | 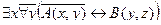
| А(x) = "x –осёл";
B(x) = "x упрям".
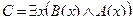
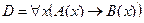
| Не все спортсмены участвовали в соревновании. |
| 30 | 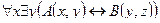
| А(x) = "x – дерево";
B(x) = "x лиственное".
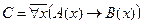
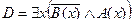
| Некоторые автобусы не останавливаются на этой остановке. |
Раздел 4. Элементы теории графов
Тема 4.1. Основы теории графов
Практическая работа №14, 15. Неориентированные и ориентированные графы.
Примеры выполнения типовых заданий.
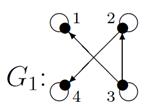
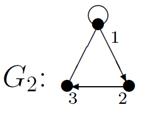
Пример №1. Для данных орграфов 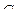 и
и 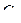 найти
найти 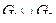 и
и  , для
, для  построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
Решение.
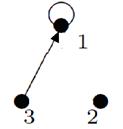
1. Объединение и пересечение графов показано на рисунке:
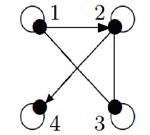
| 
|
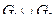
| 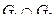
|
2. Матрица смежности для первого графа будет иметь вид:
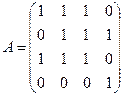
Матрица инцидентности для графа 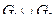 :
:
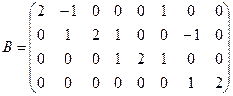
Матрица достижимости:
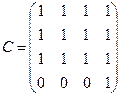 ,
,
Граф не является сильно связным. Компоненты связности:
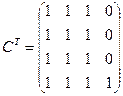 ,
, 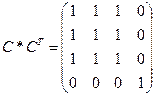 , значит сильные компоненты связности графа {1,2,3} и {4}.
, значит сильные компоненты связности графа {1,2,3} и {4}.
Пример №2. Для данного неорграфа найти матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
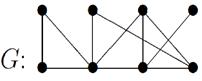
Решение.
Занумеруем вершины графа:
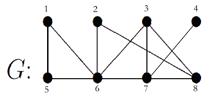
Матрица расстояний будет иметь вид:
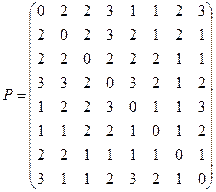
Тогда степени и эксцентриситеты вершин будут равны:
| вершина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| deg | 2 | 2 | 3 | 1 | 2 | 5 | 4 | 3 |
| ε | 3 | 3 | 2 | 3 | 3 | 2 | 2 | 3 |
Диаметр графа равен 3, радиус графа равен 2.
Центральные вершины 3, 6, 7, периферийные вершины 1, 2, 4, 5, 8.
Граф не является эйлеровым.
Пример № 3. Для данного графа найти минимальный остов.
V={a, b, c, d, e, f, g}, E={ab, ag, bc, cd, de, df, ef, fg}, r (ab) = 6, r (ag) = 9, r (bc) = 2, r (cd) = 4, r (de) = 5, r (df) = 3, r (ef) = 7, r (fg) = 8.
Решение.
Представим граф в графическом виде:
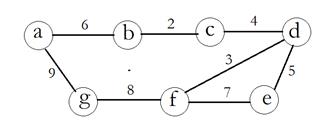
Выбираем ребро с минимальным весом (bc) = 2. Из оставшихся ребер добавляем последовательно с минимальными весами, следим за тем, чтобы не было цикла:
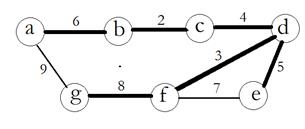
(fd) = 3, (cd) = 4, (de) = 5, (ab) = 6. Ребро (ef) не может быть добавлено, так образуется цикл: fed. Добавляем (fg) = 8. Ребро (ag) не может быть добавлено.
Полученный остов выделе на рисунке.
Задания для совместного решения.
1. Для данных орграфов 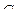 и
и 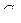 найти
найти 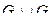 и
и 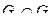 , для
, для 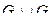 построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
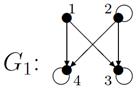 ,
, 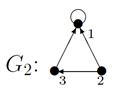
2. Для данного неорграфа найти матрицу смежности, матрицу инцидентности, матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
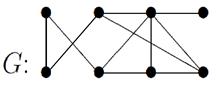
3. Для данного графа найти минимальный остов.
V={a, b, c, d, e, f, g, h}, E={ac, af, ah, bc, bh, ce, ch, de, df, ef, eh,fg, gh}, r (ac) = 2, r (af) = 9, r (ah) = 2, r (bc) = 3, r (bh) = 4, r (ce)= 7, r (ch) = 3, r (de) = 2, r (df) = 8, r (ef) = 5, r (eh) = 9, r (fg) = 1, r (gh) = 2.
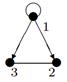
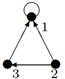
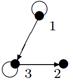
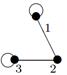
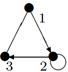
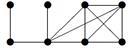
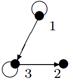
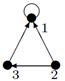
Индивидуальные контрольные задания.
1. Для данных орграфов 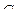 и
и 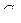 найти
найти 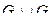 и
и 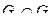 , для
, для 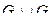 построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
построить матрицу смежности, матрицу инцидентности, матрицу достижимости. С помощью матрицы достижимости определить, является граф связным, найти его сильные компоненты связности.
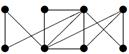
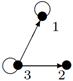
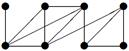
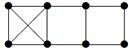
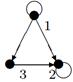
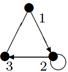
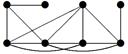
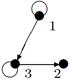
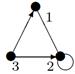
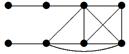
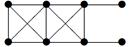
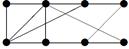
2. Для данного неорграфа найти матрицу смежности, матрицу инцидентности, матрицу расстояний. Определить степени вершин, эксцентриситеты вершин, радиус и диаметр графа, центральные и периферийные вершины. Является ли данный граф эйлеровым, если да, то найти эйлеров цикл.
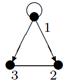
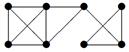
3. Для данного графа найти минимальный остов.
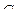
| 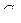
| Задание 2 | Задание 3 | |
| 1 | 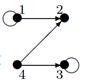
| 
| 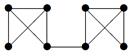
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 5, r ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 3, r ( bh ) = 3, r ( cd ) =1, r ( ch ) = 9, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 11, r ( eh ) = 2, r ( fg ) = 5, r ( fh ) = 8. |
| 2 | 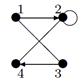
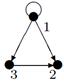
| 
| 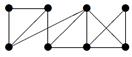
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 5, r ( ag ) = 7, r ( ah ) = 2, ( bc ) = 12, r ( bh ) = 3, r ( cd ) =10, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 11, r ( eh ) = 2, r ( fg ) = 5, r ( fh ) = 7. |
| 3 | 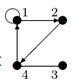
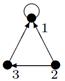
| 
| 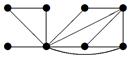
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, r ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 12, r ( bh ) = 5, r ( cd ) =10, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 5, r ( fh ) = 6. |
| 4 | 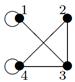
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, ( ag ) = 7, r ( ah ) = 2, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =9, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 5, r ( fh ) = 3. |
| 5 | 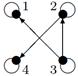
| 
| 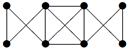
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , fh }, r ( ab ) = 2, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( fh ) = 3. |
| 6 | 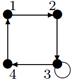
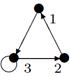
| 
| 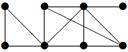
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 2, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 4, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( gh ) = 3. |
| 7 | 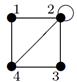
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 1, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 15, r ( gh ) = 3. |
| 8 | 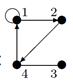
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 6, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 3, r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 9 | 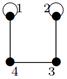
| 
| 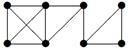
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =4, r ( ch ) = 6 r ( de ) = 9, r ( df ) = 6, r ( ef ) = 1, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 10 | 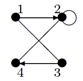
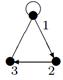
| 
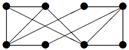
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =6, r ( ch ) = 4, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 2, r ( fg ) = 2, r ( gh ) = 9. |
| 11 | 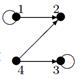
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 9, r ( bc ) = 14, r ( bh ) = 5, r ( cd ) =4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 2, r ( fg ) = 7, r ( gh ) = 9. |
| 12 | 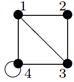
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , ag , ah , bc , bh , cd , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 8, r ( ag ) = 3, r ( ah ) = 5, r ( bc ) = 3, r ( bh ) = 8, r ( cd ) =4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 7, r ( fg ) = 2, r ( gh ) = 9. |
| 13 | 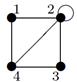
| 
| 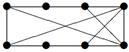
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 4, r ( ch ) = 6, r ( de ) = 9, r ( df ) = 12, r ( ef ) = 5, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 14 | 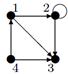
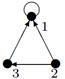
| 
| 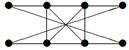
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 2, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 7, r ( ch ) = 6, r ( de ) = 1, r ( df ) = 3, r ( ef ) = 5, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 15 | 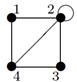
| 
| 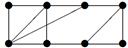
| V ={ a , b , c , d , e , f , g , h }, E ={ ac , af , ah , bc , bh , ce , ch , de , df , ef , eh , fg , gh }, r ( ac ) = 6, r ( af ) = 3, r ( ah ) = 5, ( bc ) = 3, r ( bh ) = 8, r ( ce )= 7, r ( ch ) = 11, r ( de ) = 1, r ( df ) = 3, r ( ef ) = 2, r ( eh ) = 10, r ( fg ) =7, r ( gh ) = 2 |
| 16 | 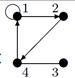
| 
| 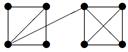
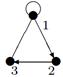
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 3, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 1, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 17 | 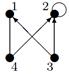
| 
| 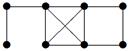
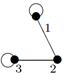
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 5, r ( cd ) =3, r ( de ) = 1, r ( ef ) = 5, r ( eg ) = 2, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
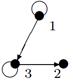
| 18 | 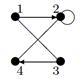
| 
| 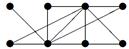
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 4, r ( bf ) = 5, r ( cd ) =3, r ( de ) = 1, r ( ef ) = 5, r ( eg ) = 2, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 19 | 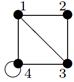
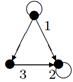
| 
| 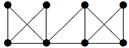
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 5, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 20 | 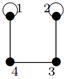
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =6, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 5, r ( gh ) = 2. |
| 21 | 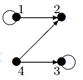
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 1, r ( ad ) = 4, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 6, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 7, r ( gh ) = 2. |
| 22 | 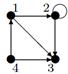
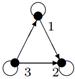
| 
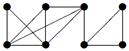
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 1, r ( cd ) =6, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 23 | 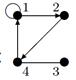
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 1, r ( gh ) = 3. |
| 24 | 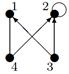
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 4, r ( eg ) = 5, r ( fg ) = 2, r ( fh ) = 3, r ( gh ) = 1. |
| 25 | 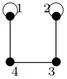
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 3, r ( ef ) = 1, r ( eg ) = 2, r ( fg ) = 1, r ( fh ) = 5, r ( gh ) = 3. |
| 26 | 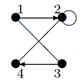
| 
| 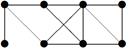
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 1, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 1, r ( ef ) = 2, r ( eg ) = 1, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 1. |
| 27 | 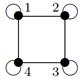
| 
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =2, r ( de ) = 1, r ( ef ) = 2, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 7. |
| 28 | 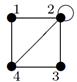
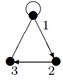
| 
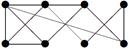
| 
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 2, r ( bd ) = 2, r ( bf ) = 4, r ( cd ) =6, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 7. |
| 29 | 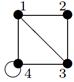
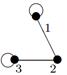
| 
| 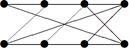
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 5, r ( bd ) = 3, r ( bf ) = 4, r ( cd ) =6, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 5, r ( fg ) = 5, r ( fh ) = 3, r ( gh ) = 1. |
| 30 | 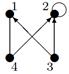
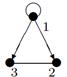
| 
| 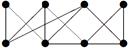
| V ={ a , b , c , d , e , f , g , h }, E ={ ab , ac , ad , bd , bf , cd , de , ef , eg , fg , fh , gh }, r ( ab ) = 4, r ( ac ) = 3, r ( ad ) = 5, r ( bd ) = 3, r ( bf ) = 1, r ( cd ) =2, r ( de ) = 4, r ( ef ) = 1, r ( eg ) = 3, r ( fg ) = 2, r ( fh ) = 3, r ( gh ) = 1. |
Раздел 5. Элементы теории алгоритмов
Тема 5.1.Элементы теории алгоритмов
Практическая работа №16. Работа машины Тьюринга
Примеры выполнения типовых заданий.
Пример №1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 0110100 найти выходное слово.
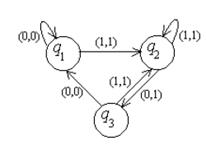
Строим таблицы функций:

Если  , то по диаграмме определяем, что
, то по диаграмме определяем, что  , если
, если  , то
, то
 и т.д.
и т.д.
Пусть дано входное слово 0110100. Найдем выходное слово:
1 шаг.  ,
,  ,
,  .
.
2 шаг.  ,
,  ,
,  .
.
3 шаг.  ,
,  ,
,  .
.
4 шаг.  ,
, 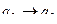 ,
,  .
.
5 шаг.  ,
, 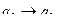 ,
,  .
.
6 шаг. 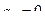 ,
, 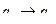 ,
,  .
.
7 шаг. 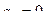 ,
, 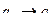 ,
,  .
.
Получаем выходное слово: 0111110.
Пример № 2. Дана машина Тьюринга с внешним алфавитом А = {a0, 1, * }, алфавитом внутренних состояний Q = {q0, q1, q2, q3}, и следующей функциональной схемой:

Задать для нее граф. Применить машину Тьюринга к слову a=11*1, начиная со стандартного начального положения.
Решение.
Граф будет выглядеть следующим образом:
Заменяем содержимое обозреваемой ячейки 1 на а0, машина переходит в новое состояние q2, головка перемещается влево. Дальнейшие действия представлены пошагово в таблице.

| 
| |
| 2 | 
| 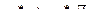
|
| 3 | 
| 
|
| 4 | 
| 
|
| 5 | 
| 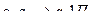
|
| 6 | 
| 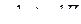
|
| 7 | 
| 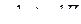
|
| 8 | 
| 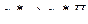
|
| 9 | 
| 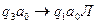
|
| 10 | 
| 
|
| 11 | 
| 
|
 Решение может быть записано в строчку как последовательность конфигураций:
Решение может быть записано в строчку как последовательность конфигураций:

Задания для совместного решения.
 1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 00111010 найти выходное слово.
1. Дан автомат с диаграммой Мура. Составить таблицы функций. Для данного входного слова 00111010 найти выходное слово.
Ответ: 11011001
2. Применить машину Тьюринга из примера №2 к слову a=1*11, начиная со стандартного начального положения.
Ответ: 111
Индивидуальные контрольные задания.
1. Дан автомат диаграммой Мура (или таблицей). Составить таблицы функций (диаграмму). Для данного входного слова найти выходное слово.
2. Дана МТ последовательностью команд (B – пустая ячейка). Составить граф и таблицу соответствия. Применить машину Тьюринга к данному слову, начиная со стандартного начального положения q1.
| Задание 1 | Задание2 | |||
| диаграмма (таблица) | Входное слово | МТ | Входное слово | |
| 1 | 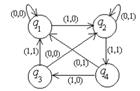
| 01000100 | aq1→aq1R bq1→bq2R Bq1→bq2R aq2→bq3L bq2→aSTOP Bq2→aq3R aq3→aq3L bq3→bq3L Bq3→bq3L | aabba |
| 2 | 
| 11111011 | 0q1→1q1L 1q1→0q2L Bq1→Bq2R 0q2→1q3L 1q2→1STOP Bq2→0q3R 0q3→1q1L 1q3→0q2L Bq3→Bq3L | 011001 |
| 3 | 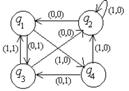
| 11000001 | *q1→1q1R 1q1→*q2L Bq1→Bq2R *q2→1q3R 1q2→1q3L Bq2→*q3R *q3→1q1L 1q3→*STOP Bq3→Bq3R | 11*111 |
| 4 | 
| 00110100 | 0q1→0q1L -q1→-q2R Bq1→Bq2R 0q2→0q3R -q2→0q3L Bq2→-q3L 0q3→0q1R -q3→0STOP Bq3→0q3R | 00--00- |
| 5 | 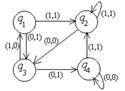
| 10010010 | 1q1→1q1L 2q1→2q2R Bq1→Bq3L 1q2→2STOP 2q2→1q3L Bq2→2q3R 1q3→1q2R 2q3→2q1R Bq3→1q3R | 111221 |
| 6 | 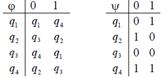
| 00001110 | 1q1→2q2L 2q1→2q1R Bq1→Bq2L 1q2→2STOP 2q2→1q3L Bq2→2q2R 1q3→1q1L 2q3→2q2R Bq3→1q3R | 111221 |
| 7 | 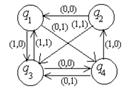
| 01110001 | mq1→tq2R tq1→mq3R Bq1→tq2L mq2→BSTOP tq2→tq3L Bq2→mq2L mq3→mq2L tq3→Bq1R Bq3→tq3R | mttmtm |
| 8 | 
| 10001110 | mq1→Bq2R aq1→mq3R Bq1→aq1L mq2→aSTOP aq2→mq3L Bq2→mq2R mq3→aq2L aq3→Bq1R Bq3→aq2R | mamaam |
| 9 | 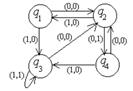
| 01111110 | 0q1→Bq3R kq1→kq1R Bq1→kq1L 0q2→0q2R kq2→kq3L Bq2→Bq1L 0q3→Bq2L kq3→0STOP Bq3→kq2R | kk000k |
| 10 | 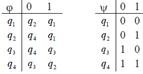
| 10000001 | *q1→+q3R +q1→*q2R Bq1→+STOP *q2→*q2R +q2→+q3L Bq2→+q2R *q3→Bq1L +q3→+q1L Bq3→+q2R | ++**++* |
| 11 | 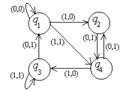
| 00110001 | xq1→xq2R yq1→yq3L Bq1→xq1R xq2→yq1L yq2→Bq2R Bq2→xSTOP xq3→yq1R yq3→yq3L Bq3→xq2L | xxyyxx |
| 12 | 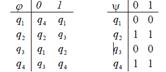
| 11001111 | 0q1→0q2R +q1→0q1R Bq1→+q3R 0q2→+q1L +q2→Bq2R Bq2→+STOP 0q3→0q3L +q3→0q1R Bq3→Bq2R | 00++0+ |
| 13 | 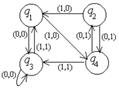
| 10010011 | xq1→xq3L +q1→+q1R Bq1→Bq2L xq2→xq1R +q2→Bq2R Bq2→+q3R xq3→xq1L +q3→+STOP Bq3→+q2L | +++xx+ |
| 14 | 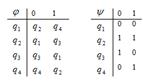
| 00100110 | 0q1→2q2R 2q1→2q2R Bq1→BSTOP 0q2→0q1R 2q2→0q1R Bq2→Bq3L 0q3→0q2R 2q3→2q2L Bq3→0q1L | 002202 |
| 15 | 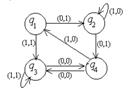
| 00010001 | *q1→1q1L 1q1→*q2R Bq1→Bq2R *q2→1q3R 1q2→1q3L Bq2→*q3L *q3→1q1R 1q3→*STOP Bq3→Bq3R | 1111*1 |
| 16 | 
| 10101100 | 0q1→2q2R 2q1→0q2R Bq1→BSTOP 0q2→0q1R 2q2→0q1R Bq2→Bq3R 0q3→2q2R 2q3→2q2R Bq3→Bq1L | 2202002 |
| 17 | 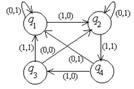
| 00000110 | nq1→nq2L oq1→oq2R Bq1→Bq2R nq2→oq1R oq2→Bq1R Bq2→nq3L nq3→nq2L oq3→BSTOP Bq3→oq1L | oonoon |
| 18 | 
| 11100011 | 0q1→1q3R 1q1→1q2R Bq1→BSTOP 0q2→0q1R 1q2→0q3R Bq2→Bq1L 0q3→0q2R 1q3→1q1L Bq3→0q1R | 110001 |
| 19 | 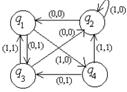
| 00100111 | 0q1→0q1L -q1→-q2R Bq1→Bq2R 0q2→-q3L -q2→0q3L Bq2→-q3L 0q3→-q1R -q3→0STOP Bq3→0q3R | 0-0-0-0-0 |
| 20 | 
| 10101010 | cq1→cq2L uq1→cq1R Bq1→Bq3L cq2→uq1R uq2→Bq3L Bq2→cq2R cq3→cSTOP uq3→uq2L Bq3→uq3R | ccuuuc |
| 21 | 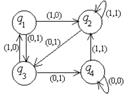
| 01010101 | 1q1→2q2L 2q1→2q3R Bq1→Bq2L 1q2→2STOP 2q2→1q3L Bq2→2q2R 1q3→1q2L 2q3→2q1R Bq3→1q3R | 112211 |
| 22 | 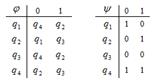
| 01001010 | mq1→tq2L tq1→mq3R Bq1→tq1L mq2→BSTOP tq2→tq3L Bq2→mq2R mq3→mq2L tq3→Bq1L Bq3→tq3R | mmttmt |
| 23 | 
| 00100010 | mq1→Bq3R aq1→mq1R Bq1→aq1L mq2→aq2R aq2→mq3L Bq2→mSTOP mq3→aq2L aq3→Bq1R Bq3→aq2R | amamma |
| 24 | 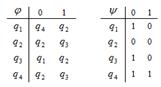
| 11011111 | 0q1→Bq3R kq1→kq2L Bq1→0q1R 0q2→0q2R kq2→kq3L Bq2→Bq2R 0q3→kq1L kq3→0STOP Bq3→kq2R | k0k0k0 |
| 25 | 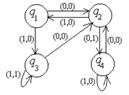
| 00011011 | *q1→+q3L +q1→*q2R Bq1→+STOP *q2→+q1L +q2→+q3R Bq2→*q2L *q3→Bq1L +q3→+q1L Bq3→Bq2R | ***+++ |
| 26 | 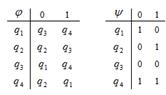
| 11111100 | xq1→xq2R yq1→yq3R Bq1→xq1R xq2→yq1L yq2→Bq2R Bq2→xSTOP xq3→yq1L yq3→Bq3R Bq3→xq2L | xxxyyy |
| 27 | 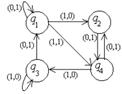
| 01110001 | 0q1→0q2L +q1→Bq3R Bq1→+q2L 0q2→+q1R +q2→Bq2L Bq2→+q2R 0q3→+STOP +q3→0q1L Bq3→0q3R | 0+0++0 |
| 28 | 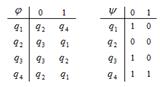
| 01101110 | xq1→+q3L +q1→+q2R Bq1→Bq1L xq2→xq1R +q2→Bq2L Bq2→+q3R xq3→xq1L +q3→xSTOP Bq3→+q2L | x++x+x |
| 29 | 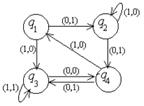
| 11010101 | cq1→cq2L uq1→cq1R Bq1→Bq3L cq2→uq1R uq2→Bq3R Bq2→cq2R cq3→cSTOP uq3→uq2L Bq3→uq3L | uucccu |
| 30 | 
| 01100100 | nq1→nq3L oq1→oq3L Bq1→Bq2L nq2→oq1R oq2→Bq3R Bq2→nq3R nq3→nq2L oq3→oSTOP Bq3→nq2L | onnoon |
Практическая работа №17. Контрольная работа №2 (итоговое тестирование).
Типовой вариант теста.
Вариант 0
| 1. | Какая формула тождественна x « y? | ||||||||||||||||||
А. 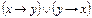
| Б. 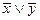
| В. 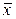 Ú y Ú y
| Г. (x®y)Ù(y®x) | ||||||||||||||||
| 2. | Выбрать операцию алгебры логики, задаваемую таблицей истинности:
| ||||||||||||||||||
А. 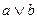
| Б. 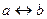
| В. 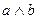
| Г. 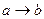
| ||||||||||||||||
| 3. | Выбрать логическую операцию, которая выражена через многочлен Жегалкина: | ||||||||||||||||||
А. 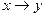
| Б. 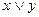
| В. 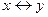
| Г. 
| ||||||||||||||||
| 4 | Представить в виде многочлена Жегалкина | ||||||||||||||||||
А. 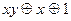
| Б. 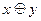
| В. 
| Г. 
| ||||||||||||||||
| 5 | Логическая функция задана таблицей истинности. Найти для нее КНФ.
| ||||||||||||||||||
А. 
| Б. 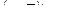
| В. 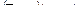
| Г. 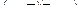
| ||||||||||||||||
| 6 | Логическая функция задана таблицей истинности. Найти для нее ДНФ.
| ||||||||||||||||||
А. 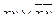
| Б. 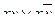
| В. 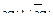
| Г. 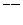
| ||||||||||||||||
| 7 | К какому из классов Поста принадлежит функция | ||||||||||||||||||
А. 
| Б. 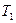
| В.S | Г. ни к одному из перечисленных | ||||||||||||||||
| 8 | Какое из равенств верно? | ||||||||||||||||||
А. x ® y º  Ú y Ú y
| Б. x ® y º x Ú y | В. x ® y º x Ù y | Г. x Û y º x Ú y | ||||||||||||||||
| 9 | Дизъюнкцией двух высказываний х и y называется высказывание… | ||||||||||||||||||
| А. ложное тогда и только тогда, когда оба высказывания х и ложны. | Б. истинное тогда и только тогда, когда истинности высказываний х и y совпадают | В. истинное тогда и только тогда, когда истинны оба высказывания х и y | Г. ложное тогда и только тогда, когда оба высказывания х и y истины. | ||||||||||||||||
| 10 | Найти среди многочленов Жегалкина линейный: | ||||||||||||||||||
А. 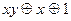
| Б. 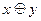
| В. 
| Г. 
| ||||||||||||||||
| 11 | Булевой функцией f (x1, x2, …, xn) называется | ||||||||||||||||||
| А. дизъюнкция простых конъюнкций. | Б. выражения, полученные из переменных x, y,… посредством применения логических операций, а также сами переменные, принимающие значения истинности высказываний | В. произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0» | Г. формула, равносильная исходной формуле логики высказываний и записанная в виде конъюнкции элементарных дизъюнкций переменных. | ||||||||||||||||
| 12 | Какие переменные в предикате ∀x2∃x5P(x1,x2,x3,x4,x5) являются связными? | ||||||||||||||||||
| А. x1,x2,x3,x4,x5 | Б. x2,x5 | В. x1,x3,x4 | Г. Р | ||||||||||||||||
| 13 | Множеству (А∩В)\С соответствует диаграмма | ||||||||||||||||||
А. 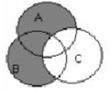
| Б. 
| В. 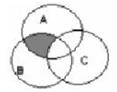
| Г. 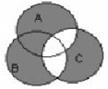
| ||||||||||||||||
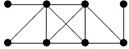
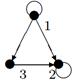
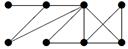
| 14 | Найти граф, соответствующий матрице смежности
| ||||||||||||||||||
А. 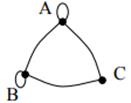
| Б. 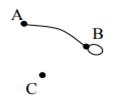
| В. 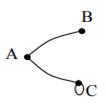
| Г. 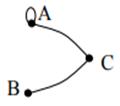
| ||||||||||||||||
| 15 | Если связи между вершинами графа характеризуются определенной ориентацией, то граф называется | ||||||||||||||||||
| А. циклическим | Б. взвешенным | В. конечным | Г. орграфом | ||||||||||||||||
Ответы к тесту:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Г | Г | Г | В | Г | Ф | А | А | А | Б | В | Б | В | В | Г |
Критерии оценивания:
«5» - 14 - 15 правильных ответов
«4» – 11-13 правильных ответов
«3» – 8 -10 правильных ответов
Типовой расчет по курсу «Дискретная математика».
Указания по выполнению типового расчета.
Типовой расчет по математическим дисциплинам выполняется в процессе изучения дисциплин.
Цели и задачи выполнения типового расчета
- Повторение и систематизация изучаемого материала;
- Контроль знаний по различным темам курса;
- Изучение дополнительной литературы и различных источников информации;
- Отработка алгоритмов решения задач;
- Систематизация самостоятельной работы студентов
Алгоритм выполнения типового расчета
Определение варианта работы. Вариант типового расчета определяется согласно порядковому номеру в списке группы по таблице.
- Получение заданий типового расчета.
- Определение списка тем, по которым выполняется типовой расчет.
- Подготовка литературы по необходимым темам.
- Изучение учебной литературы, повторение алгоритмов решения задач, оформления решения.
- Выполнение заданий в черновом варианте, консультация преподавателя.
- Оформление типового расчета, титульного листа.
- Сдача типового расчета на проверку преподавателю.
- Защита типового расчета.
- Доработка недоделок, исправление ошибок, вторичная защита.
Требования к оформлению типового расчета
- При оформлении типового расчета необходимо оформить титульный лист
- Тексты заданий переписываются полностью.
- Решение задач должно быть подробным, развернутым, с необходимыми пояснениями, ссылками на теоретический материал.
- В конце каждого задания должен быть выписан ответ.
- В конце работы должен быть указан список литературы в соответствие с требованиями по оформлению.
Требования при защите типового расчета
- При защите типового расчета студенту могут быть заданы уточняющие вопросы по теоретическому материалу, который применяется в данном расчете.
- При необходимости студент может получить задания, аналогичные тем, которые выполнялись в типовом расчете;
- Студент должен уметь пояснить решение задач, знать определения, теоремы и алгоритмы решения.
Критерии оценивания типового расчета
При оценивании типового расчета учитываются:
- Правильность решения заданий
- Обоснование решение
- Правильность и аккуратность оформления
- Использование дополнительных знаний по предмету
- Исполнительная дисциплина (своевременность сдачи)
- Качество защиты типового расчета (ответы на вопросы, решение заданий)
Типовые задания.
- Докажите тождество используя:
а. определение операций над множествами;
б. с помощью алгебры логики
в. с помощью диаграмм Эйлера.
2. Бинарное отношение Р задано на множестве В = { 1, 2, 3, 4}, Р Í В2. Изобразите Р графически и с помощью матрицы бинарного отношения. Проверьте с помощью матрицы, является ли это отношение рефлексивным, симметричным, транзитивным.
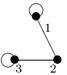
- Даны графы G 1 и G 2. Найдите G 1 Ç G 2 , G 1 È G 2. Для графа G 1 È G 2 найдите матрицы смежности, инцидентности.
- Найдите радиус и диаметр графа. Является ли этот граф эйлеровым?
- Составьте таблицу истинности для формулы.
- Проверьте, являются ли данные формулы эквивалентными с помощью
а) таблицы истинности
б) эквивалентных преобразований.
- С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ.
- Найдите сокращенную, все тупиковые и минимальные ДНФ данной булевой функции.
- Является ли полной система функций?
- Дан автомат диаграммой таблицей соответствия. Составить диаграмму Мура. Для данного входного слова найти выходное слово.
Распределение заданий по вариантам.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 11 | 1 | 12 | 21 | 32 | 43 | 54 | 65 | 76 | 87 | 98 |
| 12 | 2 | 13 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 |
| 13 | 3 | 14 | 23 | 34 | 45 | 56 | 67 | 78 | 89 | 100 |
| 14 | 4 | 15 | 24 | 35 | 50 | 57 | 68 | 79 | 90 | 91 |
| 15 | 5 | 16 | 25 | 36 | 49 | 58 | 69 | 80 | 89 | 93 |
| 16 | 6 | 17 | 26 | 37 | 48 | 59 | 70 | 78 | 88 | 92 |
| 17 | 7 | 18 | 27 | 38 | 47 | 60 | 62 | 76 | 87 | 94 |
| 18 | 8 | 19 | 28 | 39 | 46 | 59 | 64 | 74 | 85 | 95 |
| 19 | 9 | 20 | 29 | 40 | 41 | 58 | 66 | 72 | 86 | 97 |
| 20 | 10 | 11 | 21 | 32 | 43 | 57 | 68 | 79 | 84 | 94 |
| 21 | 1 | 13 | 22 | 31 | 45 | 56 | 70 | 77 | 83 | 96 |
| 22 | 2 | 14 | 23 | 34 | 47 | 55 | 61 | 75 | 81 | 99 |
| 23 | 3 | 15 | 24 | 33 | 49 | 54 | 63 | 73 | 82 | 100 |
| 24 | 4 | 16 | 25 | 36 | 42 | 53 | 65 | 71 | 90 | 99 |
| 25 | 5 | 17 | 26 | 35 | 44 | 52 | 67 | 80 | 85 | 98 |
| 26 | 6 | 18 | 27 | 37 | 46 | 51 | 69 | 71 | 86 | 96 |
| 27 | 7 | 19 | 28 | 36 | 48 | 52 | 70 | 73 | 81 | 97 |
| 28 | 8 | 20 | 29 | 39 | 50 | 53 | 62 | 74 | 82 | 95 |
| 29 | 9 | 11 | 30 | 38 | 41 | 54 | 65 | 72 | 87 | 91 |
| 30 | 10 | 15 | 21 | 32 | 50 | 59 | 64 | 72 | 85 | 99 |
Задание 1

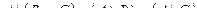
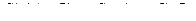
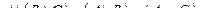
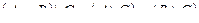
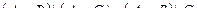
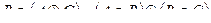
|
Задание 2 | |
| 11 | (1;1) (2;1) (2;2) (2;3) (2;4) (3;3) (4;4) |
| 12 | (1;1) (1;4) (2;2) (2;3) (3;3) (3;2) (4;1) (4;4) |
| 13 | (2;1) (3;1) (3;2) (4;1) (4;3) |
| 14 | (1;1) (1;2) (2;2) (3;3) (4;3) (4;4) |
| 15 | (1;1) (2;4) (2;1) (3;3) (4;2) (4;1) |
| 16 | (1;1) (1;4) (2;1) (3;4) (4;3) (4;1) |
| 17 | (1;3) (1;4) (2;2) (3;3) (4;3) (4;4) |
| 18 | (1;3) (1;2) (2;3) (3;2) (3;4) (4;1) |
| 19 | (1;1) (1;2) (2;2) (3;3) (4;1) (4;4) |
| 20 | (1;1) (1;3) (2;4) (3;1) (3;4) (4;3) (4;2) |
|
Задание 3 | |||||

| 
| 
| 
| ||
| 21 | 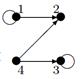
| 
| 26 | 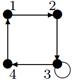
| 
|
| 22 | 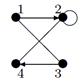
| 
| 27 | 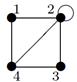
| 
|
| 23 | 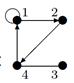
| 
| 28 | 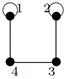
| 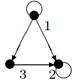
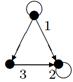
|
| 24 | 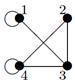
| 
| 29 | 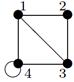
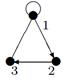
| 
|
| 25 | 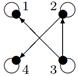
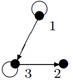
| 
| 30 | 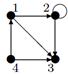
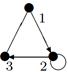
| 
|
|
Задание 4 | |||
| 31 | 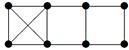
| 36 | 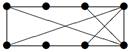
|
| 32 | 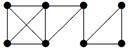
| 37 | 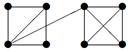
|
| 33 | 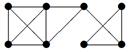
| 38 | 
|
| 34 | 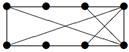
| 39 | 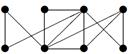
|
| 35 | 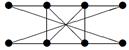
| 40 | 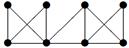
|
|
Задание 5 | |||
| 41 | 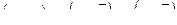
| 46 | 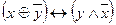
|
| 42 | 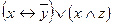
| 47 | 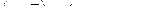
|
| 43 | 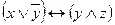
| 48 | 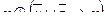
|
| 44 | 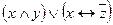
| 49 | 
|
| 45 | 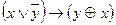
| 50 | 
|
|
Задание 6 | |||||
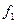
| 
| 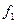
| 
| ||
| 51 | 
| 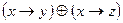
| 56 | 
| 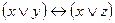
|
| 52 | 
| 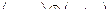
| 57 | 
| 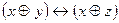
|
| 53 | 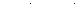
| 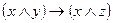
| 58 | 
| 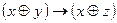
|
| 54 | 
| 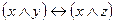
| 59 | 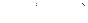
| 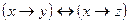
|
| 55 | 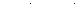
| 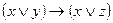
| 60 | 
| 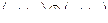
|
|
Задание 7 | |||
| 61 | 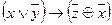
| 66 | 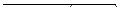
|
| 62 | 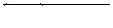
| 67 | 
|
| 63 | 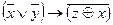
| 68 | 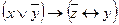
|
| 64 | 
| 69 | 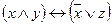
|
| 65 | 
| 70 | 
|
|
Задание 8 | |||
| 71 | 
| 76 | 
|
| 72 | 
| 77 | 
|
| 73 | 
| 78 | 
|
| 74 | 
| 79 | 
|
| 75 | 
| 80 | 
|
|
Задание 9 | |||||
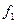
| 
| 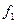
| 
| ||
| 81 | 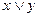
| 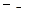
| 86 | 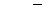
| 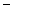
|
| 82 | 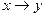
| 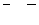
| 87 | 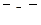
| 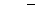
|
| 83 | 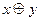
| 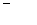
| 88 | 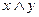
| 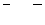
|
| 84 | 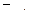
| 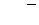
| 89 | 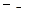
| 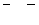
|
| 85 | 
| 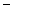
| 90 | 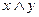
| 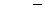
|
|
Задание 10 | |||||
| 91 | 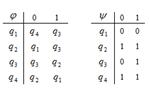
| 11000001 | 96 | 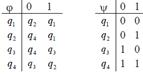
| 11111100 |
| 92 | 
| 00110100 | 97 | 
| 01110001 |
| 93 | 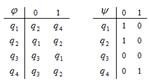
| 10010010 | 98 | 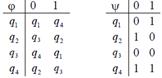
| 01101110 |
| 94 | 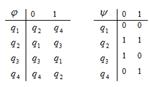
| 00001110 | 99 | 
| 11010101 |
| 95 | 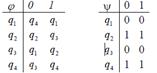
| 01110001 | 100 | 
| 01100100 |
Список используемых источников
1. Артюхина Д.Д. Элементы математической логики: учебное пособие. – Старый Оскол: СТИ НИТУ «МИСиС», 2016. – 160 с.
2. Балюкевич Э.Л., Ковалева Л.Ф., Романников А.Н. Дискретная математика: Учебное пособие, руководство по изучению дисциплины / Московский государственный университет экономики, статистики и информатики, – М., 2007. – 125 с.
3. Дискретная математика. Алгебра логики (Алгебра высказываний): метод, указания к выполнению самостоят, и контрол. работы / сост. Л.В. Балабко. – Архангельск: Изд-во ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», 2011. – 42 с.
4. Дискретная математика: практикум / сост. И.А, Сурикова; Яросл. гос. ун-т им. П.Г.Демидова. – Ярославль: ЯрГУ, 2010. – 76 с.
5. Игошин В.И. Математическая логика и теория алгоритмов: учебное пособие для студ. высш. учеб. заведений – М.: Издательский центр «Академия», 2014. – 448 с.
6. Математическая логика. Типовые расчёты: методические указания и контрольные задания / сост.: Е.С. Лоскутова, А.Д. Нахман. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2008. – 28 с.
7. Новиков Ф.А. Дискретная математика для программистов: учебник для вузов. СПб.: Питер, 2004. – 364 с.
8. Судоплатов С.В., Овчинников Е.В. Элементы дискретной математики: учебник. М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. – 280 с.
9. Усов С.В.Дискретная математика. Учебно-методическое пособие для студентов направления «Информатика и вычислительная техника». – Омск: ОмГУ, 2011. – 60 с.
Краткие теоретические сведения.
Понятие высказывания. Основные логические операции. Формулы логики. Таблица истинности и методика её построения.
Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).
То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.
Пример. “Москва – столица России” – истинное высказывание.
“5 –четное число” – ложное высказывание.
“ 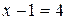 ” – не высказывание (неизвестно, какие значения принимает
” – не высказывание (неизвестно, какие значения принимает 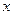 ).
).
“Студент второго курса” не высказывание (не является утверждением).
Высказывания бывают элементарные и составные.
Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.
Пример. “Число 22 четное” – элементарное высказывание.
“Число 22 четное и делится на 11” – составное высказывание.
На множестве всех высказываний определена функция истинности:
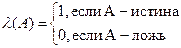
Значение λ(A) называется логическим значением или значением истинности высказывания А.
К высказываниям и буквам можно применять логические связки или логические операции. При этом получаются формулы. Формулы становятся высказываниями при подстановке всех значений букв.
Отрицание («не») есть операция перехода от высказывания А к высказыванию Ā (A), которое истинно тогда и только тогда, когда A ложно;
Конъюнкция («и») есть операция перехода от высказываний А и В к составному высказыванию А∧В, которое истинно тогда и только тогда, когда A и B истинны одновременно;
Дизъюнкция («или») – переход к составному высказыванию A∨B, которое является истинным, если истинно хотя бы одно из высказываний А и В;
Импликация («если …, то») – переход к составному высказыванию А→В, ложному, когда А истинно и В ложно, и истинному в остальных случаях;
Эквиваленция («необходимо и достаточно», «тогда и только тогда») приводит к составному высказыванию А↔В, которое истинно, если А и В одновременно истинны или одновременно ложны.
Таблица 1 – Таблицы истинности основных логических операций
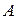
| 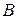
| 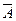
| 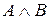
| 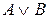
| 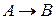
| 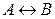
|
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Пользуясь указанными логическими связками, их истинностными таблицами, можно построить сколь угодно сложное высказывание и найти его истинностную таблицу.
Число строк истинностной таблицы, очевидно, равно 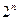 , где n – число переменных.
, где n – число переменных.
При записи формул необходимы приоритеты (очерёдность выполнения операций). Такие приоритеты обозначаются скобками. При их отсутствии сначала выполняется отрицание, затем конъюнкция, дизъюнкция, потом импликация и эквиваленция. Внешние скобки обычно опускают.
Формула называется тавтологией, если она принимает только истинные значения при любых значениях букв. Другими словами, тавтология – это тождественно истинная формула.
Формула называется противоречивой, если она принимает только ложные значения при любых значениях букв. Другими словами, противоречивая – это тождественно ложная формула.
Формула называется выполнимой, если она принимает истинное значение хотя бы на одном наборе переменных.
Формула называется опровержимой, если она принимает ложное значение хотя бы на одном наборе переменных.
Примеры выполнения типовых заданий.
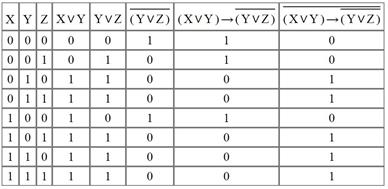
Пример 1. Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
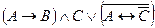
Решение.

Данная формула является выполнимой и опровержимой.
Задания для совместного решения
Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
1. 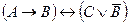
2. 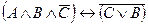
3. 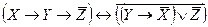
4. 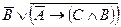
5. 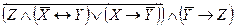
Ответы:
| 1 | 
| 2 | 
| 3 | 
| 4 | 
| 5 | 
|
Индивидуальные контрольные задания.
Составить таблицы истинности для следующих формул и указать вид формулы алгебры логики.
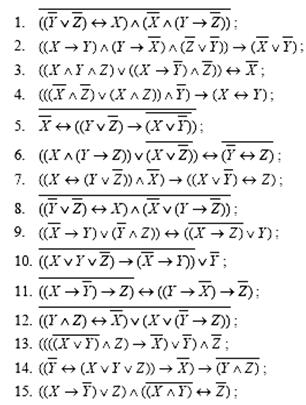
| 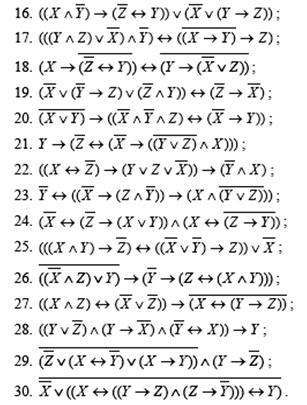
|
Практическая работа №2. Упрощение формул логики с помощью равносильных преобразований.
Дата: 2018-12-28, просмотров: 549.
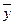
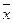
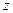
 .
.