Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Кодовая последовательность ЦК при заданной порождающей матрице G_{k , n} ( x ) и заданном информационном блоке Q ( x ) формируется по правилу 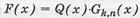, т. е. произведения вектора-строки Q ( x ), содержащего k информационных двоичных символов, на порождающую матрицу G ( x ) размером k×n. При этом, если используется каноническая (приведенно-ступенчатая) G ( x ), то будут формироваться кодовые последовательности систематического разделимого ЦК. Порождающая матрица G ( x ) строится довольно просто, если задан образующий полином Р(х) и длина кодовой последовательности п.

Пример: Сформировать кодовую последовательность ЦК с параметрами , если 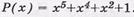 , Q(x)=x+1.

Переводим Р(х) из записи в форме полинома в двоичную форму записи, т.е. 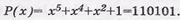Далее формируем первую строку порождающей матрицы G_5,10(х) следующим образом: двоичную последовательность 110101 дополняем справа четырьмя нулями; в результате получаем разрешенную кодовую последовательность вида 1101010000 длиной n=10 двоичных симво­лов. Следующий шаг - выполнение (k-1)=(5-l)=4 циклических сдвига двоичных символов первой строки G ( x ).

В результате получаем следующую порождающую матрицу

               

F(x)=Q(x)*P(x)=(x+1)(x⁵+x⁴+x²+1)=x⁶+x⁵+x³+x+x⁵+x⁴+x²+1=x⁶+x⁴+x³+x²+x+1 (0001011111)

или

 

                                         1101010000

                                         0110101000

F(x)=Q(x)*G_5,10(x)=00011* 0011010100 = 0001011111

                                         0001101010

                                         0000110101

Пример: Рассмотрим способ формирования кодовых последовательностей ЦК с использованием единичной матрицы и остатков от деления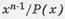

Для рассмотрения сущности формирования кодовых после­довательностей ЦК используем данные предыдущего примера.

Так как k = 5, то используем следующие единичные векторы:

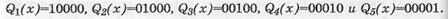
Записываем Q ₁ ( x )... Q ₅ ( x ) в виде единичной подматрицы размером (5x5).

Далее определяем проверочные символы: каждой строки по сле­дующей методике: делим 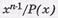и берем остатки от деления для первой строки – от первого такта деления, т.е. R ₁ ( x ), для второй строки – после двух тактов деления, т. е. R ₂ ( x ) и т. д. Полученные символы дописываем к соответствующим строкам единичной подматрицы:

 

                                         10000 10101

                                         01000 11111

F(x)=Q(x)*G_5,10(x)=00011* 00100 01011 = 0001110000

                                         00010 00011

                                         00001 10011

 

Назначение и способы построения провероч­ ной матрицы циклического кода

Проверочные матрицы H_{l , n} ( x ) ЦК могут использоваться для выбора как способов кодирования информации, так и алгоритмов декодирования. Проверочные матрицы ЦК могут быть построены с использованием порождающей матрицы G_{k , n} ( x ), единичной матрицы проверок и проверочного полинома h ( x ).

Сущность способа построения проверочной матрицы Н_l,n ( x ) c использованием канонической порождающей матрицы G_k,n(x) состоит в следующем.

Пусть задана следующая каноническая порождающая матрица ЦК с параметрами ( n , k , do )=(7,4,3) вида:

1000 101

G_4,7(x) = 0100 111

           0010 110

           0001 011

Первый столбец проверочной матрицы Н_3,7(х) для данного кода записываем, используя проверочные символы первой строки G _4,7 ( x ), а второй, третий и четвертый столбцы H _3,7 ( x ) формируем путем записи проверочных символов второй, третьей и четвертой строк G _4,7 ( x ) и далее записываем три столбца единичной подматрицы. В результате получаем следующую проверочную матрицу:

а₁а₂а₃а₄ b₁b₂b₃

1110 100

H_3,7(x) = 0111 010

          1101 001

Ненулевые символы строк проверочной матрицы определяют позиции информационных символов, участвующие в формировании проверочных уравнений. Так для построенной проверочной матрицы H _3,7 ( x ) можно сформировать следующие три проверочных уравнения: b₁= а₁Åa₂Åa₃, b₂= а₂Åa₃Åa₄, b₃= а₁Åa₂Åa_4.

Принцип построения проверочной матрицы с использова­нием единичной подматрицы и остатков от деления аналогичен принципу построения порождающей матрицы. Количество ос­татков от деления х^п+1 на Р(х) должно быть равно количеству строк единичной подматрицы.

Сущность принципа построения проверочной матрицы ЦК с использованием проверочного полинома h ( x ) состоит в следующем. Первоначально определяем проверочный полином как отношение х^п+1 на Р(х), т.е. 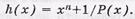Полученный полином переводим в двоичную форму записи, записываем в виде первой строки проверочной матрицы Н _{l , k} (х) и дополняем нулями до количества столбцов, равное п. Далее выполняем ( l -1) циклический сдвиг двоичных символов пер­вой строки.

Пример: Построить проверочную матрицу ЦК с пара­метрами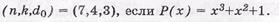

Решение:

1) определяем проверочный полином

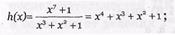
2) переводим h ( x ) в двоичную форму записи h(x) – 11101;

3) записываем 11101 в виде первой строки Н_3,7(х) и дополняем справа двумя нулевыми символами до n=7;

4) выполняя (l-1)=(3-1)=2 циклических сдвига двоичных символов первой строки Н_3,7(х) строим проверочную матрицу Н_3.7(х) следующего вида:

Проверочные уравнения:  b₁= а₁Åa₂Åa₃,

                                           b₂= а₂Åa₃Åa₄,

                                           b₃= а₃Åa₄Åb₁= а₃Åa₄Å а₁Åa₂Åa₃= а₁Åa₂Åa_4.

 

 

Способ формирования кодовых последователь­ ностей циклического кода с использованием образующего полинома

Данный способ формирования кодовых последовательно­стей ЦК находит широкое применение на практике в виду его существенной простоты. При построении ЦК с использованием образующего полинома Р(х) могут быть сформированы кодовые последовательности как систематических, так и несистематиче­ских кодов.

При формировании кодовых последовательностей несисте­ матического ЦК необходимо выполнить умножение передавае­мого информационного блока Q ( x ) степени ( k -1) на порождающий полином P ( x ) с приведением по модулю два коэффициентов при слагаемых с одинаковыми показателями степеней. Таким образом, F_i ( x )= Q ( x )* P ( x ).

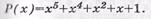Пример: Сформировать кодовую последовательность несистематического ЦК с параметрам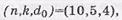и если

 

Решение:

1) выбираем информационный блок Q ( x ) следующего вида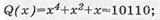

2) формируем кодовую последовательность по правилу

F(x)=Q(x)*P(x)=(x⁴+x²+x)(x⁵+x⁴+x²+x+1)= x⁹+x⁸+x⁷+x⁶+x (1111000010)

В данной кодовой последовательности нет четкого деления на блоки информационных и проверочных символов.

 

Сущность построения систематического ЦК с использова­нием образующего полинома состоит в следующем:

1) передаваемый информационный блок из k двоичных символов представляется многочленом Q ( x ) степени ( k - l );

2) многочлен Q ( x ) умножается на член Р(х) с макси­мальной степенью x^l = x^{n - k} , т.е. Q ( x ) × x^l , что эквивалентно припи­сыванию к Q ( x ) со стороны младших разрядов l = n - k нулевых двоичных символов (разрядов);

3) выполняется деление произведения Q ( x ) × x^l на образующий полином Р(х) до получения остатка R(х) со степенью меньшей максимальной степени образующего полинома Р(х). Данный остаток R(х) представляет собой сформированные проверочные символы;

4) дописать остаток R(х) к произведению Q ( x )* x^l . Следовательно, процесс формирования кодовой последовательности ЦК c использованием образующего полинома можно записать так:

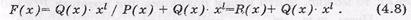
Пример:. Сформировать кодовую последовательность систематического ЦК с параметрами ( n , k , do ) – (13,8,5).

 

 

Решение:

а) так как k=8, то выбираем информационный многочлен 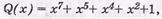 а максимальную степень образующего по­линома принимаем равной l=n - k=13-8 =5. Выбираем табулирован­ный образующий, полином вида Р(х)=х⁵+х³+1;

б) далее в соответствии с вышерассмотренными операциями получаем:

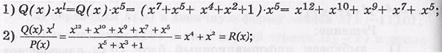
в) следовательно,

F(x) = Q(x)×x^l +R(x) = х¹²+ х¹⁰+ х⁹+ х⁷+ х⁵+ х⁴+ х² = 1011010110100.

 

 

Многотактные фильтры

 

Многотактный фильтр – устройство состоящее из некоторого числа элементов задержки и логических элементов, связанных между собой.

Значение выходного сигнала в некоторый момент t может зависеть от значения входного сигнала в этот момент, а также от значения входных и выходных сигналов в предшествующие моменты.

Многотактный фильтр называется линейным, если отклик фильтра на сумму входных сигналов равен сумме откликов на каждый из входных сигналов в отдельности.

Многотактные фильтры являются синхронными устройствами, т.к. значения всех запоминаемых символов изменяются в один и тот же момент t, называемый тактом, т.е. фиксированный отрезок t, на который элементы задержки задерживают поступающий на вход сигнал, следовательно, выходной сигнал элемента задержки на i-ом такте совпадает с входным на (i-1) такте (предыдущем).

С помощью многотактных линейных фильтров производится:

1. вычисление остатков от деления,

2. умножение сообщения на образующий полином.

Многотактный фильтр, имеющий один вход и один выход и не имеющий цепи обратной связи, производит операцию умножения.

На рисунке приведен пример структурной схемы умножения информационного полинома (на схеме обозначен А(х)) на порождающий полином (на схеме обозначен S(х)). На рисунке а приведена схема с вынесенными сумматорами, а на рисунке б со встроенными.

 

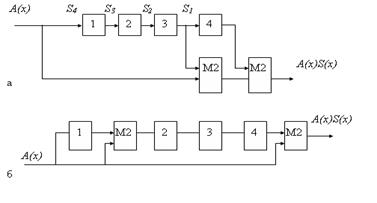
Рис. Структурные схемы для умножения полинома 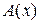 на полином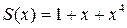

 

Многотактный фильтр, имеющий один вход и один выход, а также цепь обратной связи, выполняет операцию деления полиномов.

На рисунке приведен пример структурной схемы для деления на порождающий полином S(х). Схема для выполнения деления может быть, как и для умножения, реализована в двух вариантах: на регистрах с вынесенными сумматорами (рис. а) и встроенными сумматорами (рис. б)

 

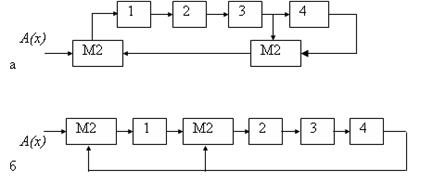
Рис. Структурные схемы для деления на многочлен S ( x )=1+ x + x ⁴