Матричные коды – это такие многомерные помехоустойчи­вые коды, которые формируются на основе использования спе­циальных матриц путем организации проверок на четность ло­гических 1 по строкам и столбцам матрицы. (Примечание: допускается организация проверок (формирование проверочных уравнений) на нечетность, а также одновременно на четность и нечетность).

В соответствии с ГОСТом 20687-82 передаваемые блоки ин­формационных, символов записываются в виде столбцов и строк матрицы выбранного размера (ранга). Первоначальная запись информацион­ных символов по строкам или столбцам не имеет принципиального значения, т.е. не сказывается на характеристиках кода. Матрицы могут быть по форме представления квадратные и прямоугольные, т.е. рангами соответственно 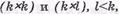где k и l количество соответственно строк и столбцов, представляющие передаваемые информационные символы.

Одновременно с записью информационных символов по строкам (или по столбцам) производится формирование провероч­ного символа (проверки); обозначим передаваемые информацион­ные символы знаком а, а проверочные символы знаком b . В об­щем виде принцип формирования матричного кода можно представить в виде следующей матрицы:

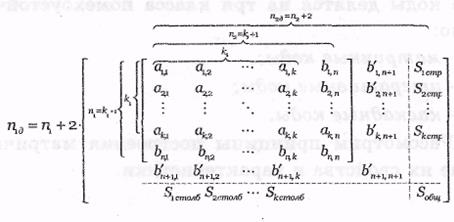
Таким образом, ранг матрицы будет равен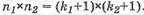

Матрицы могут быть однорядными (в каждой строке и в каждом столбце формируются по одному проверочному символу) и многорядными (в каждой строке и в каждом столбце форми­руются по два, три и более проверочных символов).

Примечание: для синхронных и асинхронных систем связи ГОСТ 20687-86 предусматривает различные правила форми­рования проверочных символов по столбцам, а именно:

- для синхронных систем связи формируется четное число логических 1;

- для асинхронных систем связи формируется нечетное число логических 1.

На приемной стороне, т.е. в декодере, формируется аналогичная матрица рангом 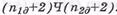. Приемная матрица формируется следующим образом. В каждом столбце и в каж­дой строке по принятым информационным символам формиру­ются проверочные символы ( b_{i , j} ) (проверки на четность), которые записываются в матрице рядом с соответствующими принятыми проверочными символами (смотри b_n,1  и b'_n+1,1 b_1,n и b '_{1, n +1} т.д.). Далее в каждой строке и в каждом столбце из принятых и вновь сформированных проверочных символов формиру­ются синдромные символы по правилу: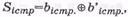

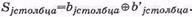
После окончания процедуры формирования синдромных символов могут быть реализованы два алгоритма декодирования матричного кода, а именно:

1) с обнаружением ошибок и повторной передачей пере­данного информационного блока;

2) с обнаружением позиций ошибочных информационных символов и их коррекцией.

Основные свойства одномерного матричного кода:

1) так как формирование проверочных символов осуществляется путем суммирования по модулю два информационных символов, то данный код относится к линейным кодам;

2) в связи с тем, что каждая строка имеет вес w≥d₀, то данный код относится к классу блоковых кодов;

3) так как строки и столбцы матрицы образуют совокуп­ность кодовых последовательностей линейно-независимых отно­сительно операции суммирования по модулю два, то данный код обладает всеми свойствами групповых кодов;

4) по способу передачи кодовых символов матричные коды могут быть как систематическими, так и несистематическими.

Параметры одномерного матричного кода.

1) N_m=n₁×n₂ – длина кодовой последовательности, где 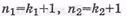– со-

ответственно количество строк и столбцов.  

 При 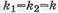,  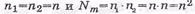двоичных символов;

2) 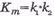 – количество информационных символов, где k₁ и k₂ – соответственно ко­личестве «информационных» строк и «информационных» столбцов. При 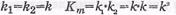двоичных символов;

3)   R_m= K_m/N_m=k₁/n₁×k₂/n₂ – скорость передачи кода,

4) l _т=N_m-K_m -абсолютная избыточность кода,

5) r_т=(1-R_m)*100% - относительная избыточность кода,

6) d _{0 m} - минимальное ко­довое расстояние, 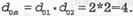 Введение одного проверочного символа в по­следовательность простого безызбыточного кода, т.е. в блок из k информационных символов, позволяет обнаруживать однократ­ные и нечетные ошибки, а в соответствии с теорией кодирова­ния, для обнаружения ошибки d₀ должно быть равно или более  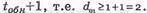Аналогично определяется d₀₂ по столбцам матрицы. Следовательно, одномерный матричный код имеет  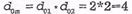и позволяет обнаруживать двукратные ошибки 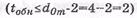или исправлять однократные ошибки

Для обнаружения и коррекции ошибочных информационных символов используются сформированные синдромные сим­волы Sij строк и столбцов, и реализуется следующее правило:

- если при приеме информации ошибочным будет только один информационный символ, то синдромные символы данной строки и столбца будут ненулевыми, т.е. равны 1;

- для коррекции ошибочного символа необходимо опреде­лить его позицию в матрице, которая, как легко установить, находится на пересечении соответствующей строки и столбца с ненулевыми синдромными символами, т.е. S_i и S_j .

7) Р_{н.ош т} – вероятность необнару­женной ошибки

Матричный код с одной провер­кой на четность по строкам и столбцам обладает низкой корректи­рующей способностью. Для повышения корректирующей способности данного кода необходимо запись (кодирование) информации выполнять по строкам, а считывание кодовых символов выполнять по столбцам, или наоборот. В этом случае будет обеспечиваться обнару­жение групповых ошибок кратностью t_n.обн= n_1д двоичных символов. Об­наружение пакетных ошибок кодом обеспечивается за счет перемежения (разноса) кодовых символов; перемежение кодовых символов позволяет преобразовать пакет ошибок в одиночные ошибки.

Достоинствами матричного кода с формированием одиноч­ных проверок на четность по строкам и столбцам являются мини­мальная сложность аппаратурной и программной реализации. Не­ достатками кода являются высокая избыточность и низкая корректирующая способность.

С целью повышения корректирующей способности одно­мерных матричных кодов были разработаны двумерные мат­ричные коды, а именно:

а) матричный код с формированием двух проверочных символов (на чет и нечет) по строкам и столбцам матрицы;

б) матричный код с формированием проверочных симво­лов (на чет) по строкам, столбцам и диагоналям матрицы.

Принцип построения матричного кода с формированием проверок на четность по строкам, столбцам и диагоналям

В соответствии с ГОСТом 20687-85 данный способ форми­рования матричного кода носит название способа формирования матричного кода с диагональными проверками. Сущность дан­ного способа построения матричного кода рассмотрим по сле­дующей условной матрице

Первоначально по информационным символам (на матри­це – это большие точки) формируются проверочные символы по строкам и столбцам (на матрице кружки – под номерами I). Затем формируются проверочные символы с использованием диагональных информационных символов, начиная с информа­ционных символов главной диагонали (на матрице эта про­цедура обозначена сплошными стрелками). Сформированный первый проверочный символ диагонали записывается на по­следнюю позицию первой строки (столбец под номером II). За­тем суммируются по модулю два информационные символы следующей диагонали (на матрице - это будет нижняя диа­гональ и обозначенная штрихпунктирной линией; в принципе можно «двигаться» по матрице и вверх); проверочные символы столбцов не используются в формировании диагональных про­верок. В качестве «недостающих» информационных символов используются проверочные символы строк. Сформированный второй проверочный символ диагональной проверки записыва­ется на последнюю позицию второй строки. Остальные прове­рочные символы формируются аналогичным способом.

На приемной стороне из принятых информационных сим­волов аналогичным способом формируются проверки на чет­ность по строкам, столбцам и диагоналям. Сформированные проверочные символы суммируются по модулю два с принятыми проверочными символами и формируют, таким образом, синдромные символы строк, столбцов и диагоналей.

Обнаружение и коррекция ошибок проводятся следующим образом: первый ошибочный информационный символ определяет­ся на пересечении строки и столбца с ненулевыми синдромными символами, который при считывании инвертируется; второй ошибочный информационный символ определяется и корректируется аналогичным способом, только его позиция определяется на пересечении соответствующих позиций ненуле­вых синдромных символов диагонали и столбца.

Таким образом, данный матричный код обеспечивает кор­рекцию ошибок длинной  бита и, следовательно, 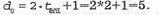 Длина кодовой последовательности  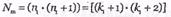двоичных, символов, а количество ин­формационных символов определяется равенством  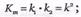при k₁=k₂. В общем виде данный матричный код записывается следующим образом:

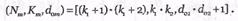
Формирование дополнительных проверок с использовани­ем информационных символов диагоналей матрицы справа на­лево позволяет построить матричный код с минимальным кодо­вым расстоянием 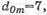т.е. матричный код, корректирующий трехкратные ошибки. Дальнейшим развитием матричных кодов было открытие итеративных кодов.