Важнейшим недостатком систематических линейных блоковых кодов (СЛБК) является высокая трудоемкость их построения при длине кодовой последовательности n≥31 двоичный символ и коррекции ошибок кратностью toш≥3 двоичных символа. Поиск более простых принципов построения СЛБК привел к открытию нового широкого класса групповых линейных блоковых кодов, получивших название циклических кодов (ЦК).
Циклические коды являются подклассом в классе линейных блоковых кодов. Свое название коды получили из-за основной операции построения кодовых последовательностей ( Fi ( x )) – циклического сдвига (перестановки) двоичных символов разрешенных кодовых последовательностей.
Циклическим кодом называется линейный блоковый код, который представляет собой конечное множество, замкнутое относительно операции циклического сдвига кодовых последовательностей, образующих данный код.
Кодовую последовательность ЦК в общем виде можно записать так:
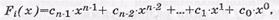
где х - формальная переменная,
п-1, п-2 ,..., 1, 0 — показатели степеней, в которые возводятся основания кодов, и одновременно порядковые номера, которые занимают двоичные символы (разряды) кодовой последовательности, начиная со старшего и заканчивая нулевым;
ci - коэффициенты формальной переменной, которые могут принимать значения или быть равными логической 1 (ненулевой член Fi ( x )) или логического 0 (нулевой член Fi ( x )). Например, 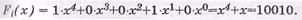
Представление кодовых последовательностей в виде полиномов позволяет установить однозначное соответствие между ними и свести действия над кодовыми последовательностями к действиям над полиномами: умножение, сложение, деление и вычитание этих полиномов производится по обычным правилам алгебры, но коэффициенты С одинаковыми степенями х суммируются по модулю два.
Уточним сущность понятия циклического сдвига или циклической перестановки двоичных символов кодовой последовательности.
Пусть 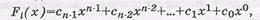 то циклический сдвиг на один разряд дает
то циклический сдвиг на один разряд дает 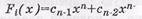
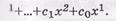 Чтобы степень новой кодовой последовательности Fi ( x ) не превышала (п-1), член сп-1хп заменяется единицей, поэтому
Чтобы степень новой кодовой последовательности Fi ( x ) не превышала (п-1), член сп-1хп заменяется единицей, поэтому 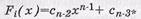
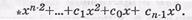
Например, пусть 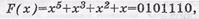 при n =7 двоичных символов. (Заметим, что запись кодовой последовательности в виде многочлена, а затем перевод ее в двоичную форму записи, не всегда определяет длину кодовой последовательности n. Например, при п=5, многочлен F ( x ) = х2+1=101, т.е. n=3, что неверно. В таких случаях надо дописать старшие нулевые символы, т.е. F ( x )= x 2 +1=00101, что дает п=5 двоичным символам).
при n =7 двоичных символов. (Заметим, что запись кодовой последовательности в виде многочлена, а затем перевод ее в двоичную форму записи, не всегда определяет длину кодовой последовательности n. Например, при п=5, многочлен F ( x ) = х2+1=101, т.е. n=3, что неверно. В таких случаях надо дописать старшие нулевые символы, т.е. F ( x )= x 2 +1=00101, что дает п=5 двоичным символам).
Сдвигаем F ( x ) на один разряд (символ) влево, и получаем F ( x ) =1011100=х6+ х4+ х3+х2. Очевидно, что xl ( x 5 + x 3 + x 2 + x )= x 5 + x 4 + x 3 + x 2 . Отсюда вытекает второе определение ЦК, а именно, циклический код – это код, для которого циклический сдвиг двоичных символов разрешенной кодовой последовательности влево или вправо на один, два,...., ( k -1) символов вновь приводит к формированию разрешенной кодовой последовательности.
Таким образом, циклическую перестановку двоичных символов разрешенной кодовой последовательности можно рассматривать как умножение F ( x ) на х при первом сдвиге, на х2 при втором сдвиге и т. д., что можно в общем виде записать или представить так:
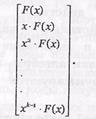
Таким образом, можно сделать следующие выводы:
1. ЦК - это такой линейный код, который обладает свойством цикличности кодовых последовательностей, т.е. когда каждая разрешенная кодовая последовательность содержит ее циклическую перестановку;
2. ЦК относятся к групповым линейным кодам, если они образуются путем умножения каждой последовательности равнодоступного (простого) кода, выраженных в виде многочлена Q ( x ) с максимальной степенью ( k -1), на некоторой полином Р(х) степени l=n - k .
Информационный полином: Q(x)=ak-1xk-1+ ak-2xk-2+…+ a0x0
Порождающий (образующий) полином: P(x)=bl xl+ al -1 xl -1+…+ b0x0
Разрешенные кодовые последовательности кода Краз = 2к образуют циклическую подгруппу Кобщ = 2п, отличающуюся тем, что все элементы подгруппы имеют общее свойство делимости на полином Р(х), получивший название образующего или порождающего полинома.
В качестве образующего полинома используются полиномы, обладающие следующими свойствами:
1. образующий полином Р(х) должен быть делителем двучлена хп+1;
2. образующий полином не должен раскладываться на сомножители более низких степеней, и должен делиться без остатка на самого себя и на 1, т.е. на х°;
3. максимальная степень образующего полинома должна быть равной l = n - k , т.е. соответствовать количеству проверочных символов используемого кода.
Свойства циклических кодов
ЦК обладают всеми свойствами СЛБК, а также имеют, ряд дополнительных свойств.
К основным свойствам ЦК относятся:
1. Вес разрешенной кодовой последовательности wкп≥d0;
2. Вес проверочной части разрешенной кодовой последовательности wпр.ч.≥d0-1;
3. Сдвиг кодовых символов разрешенной кодовой последовательности влево или вправо на один, два,..., ( k -1) символ вновь приводит к разрешенной кодовой последовательности. Если же при циклическом сдвиге всегда будет получатся кодовая последовательность нового кода, то такой код будет называться квазициклическим; данные коды имеют несколько большую корректирующую способность и сложность реализации, чем ЦК;
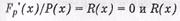 4. Разрешенная кодовая последовательность без ошибок Fp'(x) при делении на полином Р(х) дает нулевой остаток ≠0 при наличии ошибок;
4. Разрешенная кодовая последовательность без ошибок Fp'(x) при делении на полином Р(х) дает нулевой остаток ≠0 при наличии ошибок;
5. Сумма по модулю два символов двух, трех,..., (k-1) разрешенных кодовых последовательностей вновь образует разрешенную кодовую последовательность;
6. Двучлен вида хп+1 должен делиться на порождающий полином Р(х) без остатка и результат дает проверочный полином h ( x ) =(хп+1)/Р(х. Произведение h ( x )* P ( x )=хn+1=0, а потому полиномы h ( x ) и Р(х) рассматривается как ортогональные и операция деления (хп+1)/Р(х) используется в основе построения алгоритмов декодирования;;
7. Двучлен ЦК вида хп-1 можно разложить на множители
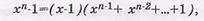
Пример:. Разложить двучлен хп-1=х7-1 на множители.
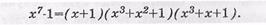 |
Двучлен х7-1 раскладывается на следующие многочлены:
Из данного выражения видно, что можно образовать шесть делителей для двучлена х7-1, путем комбинирования полученных трех сомножителей. Следовательно, для двучлена x 7 -1 существует шесть разных двоичных линейных ЦК со следующими образующими полиномами и параметрами:
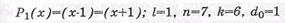 – простой код: l , k , n и tисп ( t исп -кратность исправленных ошибок) - измеряются в двоичных символах;
– простой код: l , k , n и tисп ( t исп -кратность исправленных ошибок) - измеряются в двоичных символах;
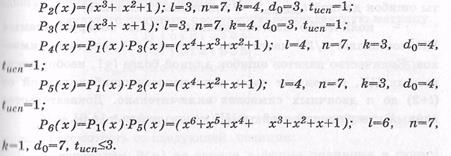
ЦК, задаваемые образующими полиномами Р1(х), P 2 ( x ) и Р3(х), относятся к классу ЦК Хэмминга. ЦК, задаваемые полиномами Р4(х), P 5 ( x ) и Р6(х), являются двойственными кодами Хэ мминга и называются кодами максимальной длины.
Корректирующая способность групповых СЛБК зависит от вида (структуры) образующего полинома, т.е. от количества ненулевых членов данного полинома и его максимальной степени l = n - k . В соответствии с этим можно отметить следующие свойства ЦК:
а) обнаруживающих ошибки:
- ЦК, образующий полином которого имеет более одного члена и не имеет общего множителя х, обнаруживает все одиночные ошибки и любое нечетное число ошибок. Простейшим образующим полиномом ЦК, обладающими данными свойствами, является полином вида Р(х)=1+х;
- ЦК, образующий полином которого имеет вид р(х)=1+хс, обнаруживает любое нечетное число ошибок. Доказательство этого утверждения становится ясным, если образующий полином представить в следующем виде
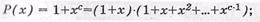
б) обнаруживающих и корректирующих ошибки: в виду того, что полином Р(х)=1+хс нацело делится на 1+х, то согласно предыдущему свойству ЦК обеспечивает обнаружение любого нечетного количества ошибок;
- ЦК, образующий полином которого имеет максимальную степень l =п-к, обнаруживает любой пакет ошибок длиной 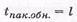 и менее двоичных символов или корректирует пакеты ошибок длиной
и менее двоичных символов или корректирует пакеты ошибок длиной 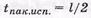 двоичных символов;
двоичных символов;
- количество пакетов длиной l +1, не обнаруживаемых ЦК, составляет 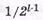 части всех пакетов (l+1) двоичных символов.
части всех пакетов (l+1) двоичных символов.
Количество пакетов ошибок длиной более l +1, необнаруживаемых ЦК, составляет часть всех пакетов ошибок длиной от ( l +2) до n двоичных символов включительно.
Способ построения кодовых последовательно стей с
Дата: 2018-12-28, просмотров: 946.