Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Операция кодирования информации линейным кодом заключается в умножении информационного вектора A_k размерностью k на порождающую матрицу G ( x ); в результате получаем вектор

F(x) = A_k (x) × G(x).

 

Кодовую последовательность на выходе кодера можно записать в виде:

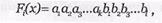
где a₁a₂a₃...а_k - информационные символы (логические 1 и 0),

       b₁b₂b₃...b₁ - проверочные символы (логические 1 и 0).

Проверочные символы b₁b₂b₃...b_l формируются путем суммирования по модулю два информационных символов, стоящих на определенных позициях.

Алгоритм формирования проверочных символов в общем виде можно записать так:

где c_j1c_j2...c_jk- коэффициенты принимающие значение логических 1 и 0.

 

Пример: A_k ( x )=1010

        1 0 0 0 1 0 1                                              

G(x)=0 1 0 0 1 1 1                                                  

        0 0 1 0 1 1 0                                                  

        0 0 0 1 0 1 1                                              

                                                                   1 0 0 0 1 0 1

Следовательно, F ( x )= A_k ( x ) × G ( x )=[1010]* 0 1 0 0 1 1 1 = [1010 011]                                              

                                                                            0 0 1 0 1 1 0                                              

                                                                            0 0 0 1 0 1 1                                                  

 

 

Рассмотрим построение и реализацию устройства кодирования ЛБК (7,4).

Порождающая и проверочная матрицы этого кода имеют вид:

        а₁а₂а₃а₄ b₁b₂b₃

        1 0 0 0 1 0 1                                      1 1 1 0 1 0 0                                                         

G(x)=0 1 0 0 1 1 1                             H(x)=0 1 1 1 0 1 0                                             

        0 0 1 0 1 1 0                                      1 1 0 1 0 0 1                                                              

        0 0 0 1 0 1 1                                                

                                                   

Этот код имеет d=3 и исправляет все одиночные ошибки и обнаруживает двойные. Символы а₁,а₂,а₃,а₄ – информационные символы, b₁,b₂,b₃ – проверочные.

По матрице запишем проверочные уравнения:

b₁= a₁Åa₂Åa₃

b₂= a₂Åa₃Åa₄

b₃= a₁Åa₂Åa₄

Таким образом, кодер состоит из (n-k)=7-4=3 сумматоров по модулю два, выходы которых соответствуют (n-k) проверочным символам.

Устройство кодирования линейного группового кода (7, 4) приведено на рисунке.

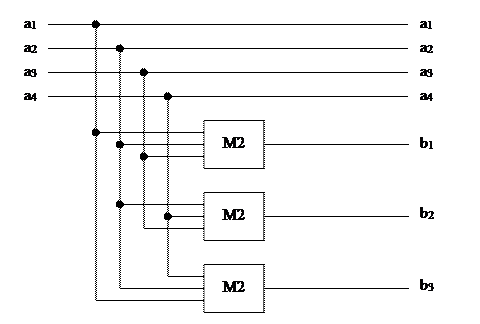
Рисунок – Кодер линейного группового кода (6, 3)

 

Пусть подается сообщение (а₁,а₂,а₃,а₄)=1001. Тогда слово, передаваемое в канал связи, имеет вид (1001 110).

 

Синдромное декодирование

 

Декодирование более сложный процесс, чем кодирование.

Декодирование линейных групповых кодов основано на следующем свойстве: Проверочная H(х) и порождающая G(х) матрицы удовлетворяют соотношению G(х)*H^t(х)=0, где H^t(х) - транспонированная проверочная матрица.

Если в принятом слове F(х) отсутствуют ошибки, то матричное произведение равно нулю.

F(х)*H^t(х)= A_k(x)*G(x)*H^t(х)= A_k(x)*0=0

Ecли же при передаче информации возникли ошибки, то (F+E)*H^t=F*H^t+E*H^t=0+E*H^t=E*H^t=S – синдром, где E – вектор ошибки. Длина синдрома равна (n-k). Ненулевая величина синдрома свидетельствует о наличии ошибки. Если различным ошибкам соответствуют различные синдромы, то по виду синдрома можно определить вид ошибки и, следовательно, исправить ее.

Этапы декодирования:

1. По принятому слову

(3)

 F(x)^* вычисляется синдром S_j (х):

S_j (x)= F(x)^* × H^t(x).

2. По синдрому S_j ( x ) находится вектор ошибок E.

3. Из принятого вектора F(x)^* вычитается вектор ошибок; в результате получаем переданное слово, F(x).

Синдромный декодер состоит из схемы, вычисляющей (n-k)-разрядный синдром, дешифратора и корректирующих сумматоров по модулю два. Схема вычисления синдрома производит умножение принятого вектора на матрицу H^t(x). При отсутствии ошибок синдром равен нулю. Если синдром не равен нулю, то возбуждаются соответствующие выходы дешифратора и сигналы с ошибочных разрядов исправляются на корректирующих сумматорах.

Схема синдромного декодера кода (6, 3) представлена на рисунке.

 

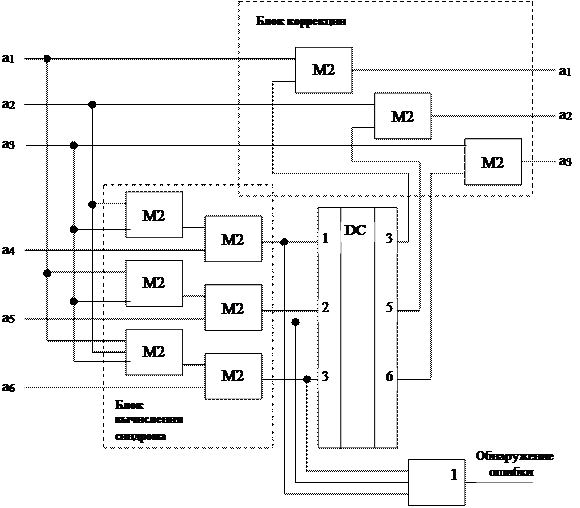Рисунок – Схема синдромного декодера кода (6, 3)

 

Пусть F(x)=111 001, например, ошибка произошла в первом разряде, т.е. принятое слово имеет вид F(x)^*=(011 001).

Вычислим синдром S_j(x)= F(x)^* × H^t(x).

       а₁а₂а₃ а₄а₅а₆

      0 1 1 1 0 0                        011

H(x) =1 0 1 0 1 0            H^t(x)= 101         S_j(x)= F(x)^* × H^t(x)=011

      1 1 1 0 0 1                        111

                                                     100

                                            010

                                            001

Синдром равен 011 (это первая строчка матрицы H^t(x), следовательно, ошибка произошла в первом разряде) и на первом выходе дешифратора должен появиться единичный сигнал, который исправит на первом корректирующем сумматоре ошибочный сигнал на противоположный – правильный. Это обеспечит получение на выходе приемника сигнала A_k(x)=111, который и передался в канал связи.

В том случае, если требуется только обнаружение ошибок, то сигналы с выхода схемы вычисления синдрома заводится на схему ИЛИ. На выходе схемы ИЛИ будет единичный сигнал в случае ненулевого синдрома, что свидетельствует о наличии ошибок в принятом сообщении.

Декодирование по синдрому применяется для коррекции ошибок малой кратности. Основная трудность при декодировании по синдрому связана с ''проблемой селектора'', который по синдрому должен однозначно установить разряды, в которых произошли ошибки, т. е. определить вектор ошибок E.

 

Мажоритарное декодирование

Способ мажоритарного декодирования привлекает как простотой описания, так и невысокой сложностью схемной реализации. Идея мажоритарного декодирования линейного кода базируется на системе проверочных равенств, а именно, в кодах с мажоритарным декодированием каждый символ может быть выражен через другие символы несколькими способами. Это позволяет для определения истинного значения символа воспользоваться принципом большинства (мажоритарным принципом).

Существует три способа построения систем проверочных уравнений при мажоритарном декодировании:

– системы с разделенными проверками;

– системы с l -связанными проверками;

– системы с квазиразделенными проверками.

В системах с разделенными проверками некоторый символ, относительно которого разделяется система уравнений, входит во все уравнения. Любой другой символ входит не более чем в одну проверку. Отсюда следует, что для коррекции t ошибок система должна состоять из (2t + 1) уравнений и иметь на столько же входов мажоритарные элементы.

Пример: Пусть имеется код (6; 3), задаваемый следующей проверочной матрицей:

                                                                    а₁а₂а₃ а₄а₅а₆

                                                              0 1 1 1 0 0

                                                   H(x) =1 0 1 0 1 0

                                                              1 1 1 0 0 1

 

Запишем систему уравнений:

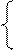а₄= a₂Åa₃

а₅= a₁Åa₃

а₆= a₁Åa₂Åa₃

 

Из этой системы можно записать систему проверочных равенств, где равенство а_i=а_i называется уравнением истинности или тривиальным.

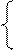 Для a₁: a₁= a₃Åa₅

             а₁ = а₂Åa₃Åa₆=а₄Åa₆

             а₁= a₁

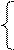Для a₂: a₂= a₃Åa₄

             а₂ = а₁Åa₃Åa₆=а₅Åa₆

             а₂= a₂

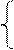Для a₃: a₃= a₂Åa₄

             а₃ = а₁Åa₅

             а₃= a₃

 

Видно, что каждый из принятых символов a_i входит в данные системы один раз, и, следовательно, если он ошибочен, то ошибочным будет одно из трех уравнений системы; два остальных – правильны. По большинству правильных проверок мажоритарный элемент принимает правильное решение об оценке состояния разряда.

С ростом числа корректируемых ошибок растет число уравнений в системе и, следовательно, увеличивается сложность мажоритарного элемента.

Декодер для кода (6,3) требует шесть сумматоров по модулю два и три мажоритарных элемента.

Схема мажоритарного декодера кода (6, 3) представлена на рисунке.

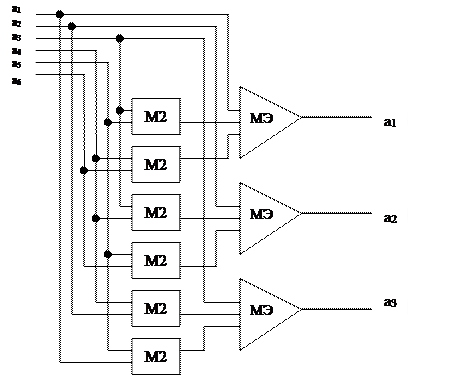
Рисунок  – Схема мажоритарного декодера кода (6, 3)

 

Достоинства мажоритарного декодирования: простота реализации, высокая скорость декодирования.

Недостатки: такие декодеры могут декодировать малый класс кодов.