К настоящему моменту времени разработано большое количество классов помехоустойчивых кодов, которые отличаются принципом построения, основанием кода ( q ), кодовым расстоянием (d₀), избыточностью (r), структурой, функциональным назначением, алгоритмами декодирования, способом передачи кодовых символов и т.д.

Для лучшего понимания и практического использования помехоустойчивых кодов вводят классификацию кодов, по характерным признакам их отличия. Наиболее широко используется следующая структура классификации (рис.):

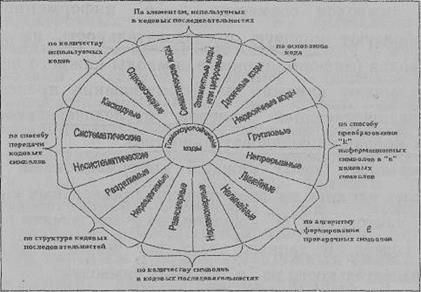
Рис. Структурная схема классификации помехоустойчивых кодов

1. По форме представления передаваемой информации — помехоустойчивый код можно разделить на две группы или на два способа представления информации, а именно: семантические коды и элементные (цифровые, дискретные) коды.

Семантические коды - используют короткие комбинации букв, обозначающие целые фразы, например, SOS - сигнал опасности, ТТТ - сигнал безопасности и т.д., а также сюда вхо­дят, так называемые Z-коды и Q-коды, которые находят приме­нение в радиосвязи, например, ZSU - ваши сигналы неразборчивы, QKM — мне мешают на этой волне и т. д.

Элементные (дискретные) коды - характеризуются тем, что каждому символу источника присваивается определенное число в заданной системе счисления и которое отображается соответствующей кодовой последовательностью, например, 10, 00 или 100, 000; 010 и т.д. Здесь элемент - "1" и "0";

2. По основанию кода или по количеству единичных элементов, используемых для формирования кодовой последовательности, коды делятся на двоичные т.е. q=2 и недвоичные, когда q >2.

3. По способу преобразования " k " информационных символов в " n " кодовых символов делятся на блоковые и непрерывные. В блоковых кодах из "к" информационных символов формируется "l" проверочных символов и " l " проверочных символов совместно с " k "  информационными символами образуют кодовую последовательность из n =( k + l ) кодовых символов (информационные символы каждого входного блока не оказывают влияния на формирование проверочных символов предшествующей кодовой последовательности и последующих кодовых последовательностей).

В непрерывных кодах каждый информационный символ может оказывать влияние на формирование проверочных символов в течение "т" тактов, где " m " - количество ячеек памяти регистра сдвига (RG) кодера. В данных кодах нет четкого деления на кодовые последовательности из "п" кодовых символов;

4. По алгоритму формирования проверочных символов — на линейные и нелинейные. В линейных кодах проверочные символы формируются путем суммирования по модулю два информационных символов, стоящих на определенных позициях. В нелинейных кодах проверочные символы формируются путем суммирования информационных символов по модулю отличному от два;

5. По количеству символов в кодовых последовательностях — на равномерные и неравномерные коды. В равномерных кодах все кодовые последовательности помехоустойчивого кода имеют одинаковую длину, т.е. " n "= const . У неравномерных кодов один и тот же помехоустойчивый код может иметь кодовые последовательности с разной длиной, т.е. "п"≠сопst;

6. По структуре кодовых последовательностей – на разделимые и неразделимые. К разделимым кодам относятся такие помехоустойчивые коды у которых есть четкое деление на блоки из k информационных символов, l - проверочных символов и на кодовые последовательности из п символов; такое деление справедливо для всех кодовых последовательностей. К неразделимым кодам относятся такие коды, у которых нет четкого деления на информационные, проверочные блоки и на кодовые последовательности;

7. По способу передачи кодовых символов – на систематические и несистематические. В систематических кодах в канал связи первоначально передается информационные символы (блок из k информационных символов), а затем блок из l проверочных символов. В систематических кодах сохраняются статистические связи между k информационными символами данной кодовой последовательности. В несистематических кодах нет четкого деления на блоки информационных символов и проверочных и, следовательно, нет статистической связи между информационными символами и в канал связи кодовые символы передаются по "псевдослучайному закону", т.е. может передан(ы) проверочный(е) символ(ы), например, два проверочных символа, а затем переданы три информационных символа, а затем один проверочный, два - информационных и т.д. Примером несистематических кодов являются коды Плоткина и коды с постоянным весом (с равным количеством логических 1).

К систематическим кодам, в первую очередь, относятся двоичные равномерные групповые линейные коды БЧХ, Файра, сверточные коды и др.

8. По количеству используемых помехоустойчивых кодов – на однокаскадные и каскадные. Однокаскадные коды используют только один помехоустойчивый код того или иного класса, а в противном случае помехоустойчивые коды называются каскадными, которые могут быть  2-х каскадные (два кода, например, один тип помехоустойчивого кода - блоковый, а второй - сверточный), 3-х каскадные -  три помехоустойчивых  кода и т. д.

 коды: общие сведения, основные свойства

Среди всех кодов наиболее полно к настоящему времени изучены линейные коды. Эти коды называются также систематическими или групповыми. Рассмотрим эти определения подробнее.

Группой называется множество элементов Г, для которых определена некоторая операция (сложения или умножения) и выполняются следующие аксиомы:

1. Если операция применена к двум элементам группы, то результат операции является также элементом группы, т.е. если а, b принадлежат Г то а+b также принадлежит Г для операции сложения и а*b принадлежит Г для операции умножения.

2. Для любых трех элементов группы a, b, c выполняется ассоциативный закон:

(a+b)+c=a+(b+c) – для операции сложения

a*(b*c)=(a*b)*c – для операции умножения

3. Существует нейтральный элемент. Если в качестве операции взято сложение, то нейтральный элемент называется нулем и удовлетворяет уравнению а+0=а. Если в качестве операции взято умножение, то нейтральный элемент называется единицей и удовлетворяет выражению а*1=а.

4. Каждый элемент группы обладает обратным элементом таким, что а+(-а)=0 для сложения, а*а^-1=1 для умножения.

Группа с операцией сложения называется аддитивной, а с операцией умножения – мультипликативной.

Некоторое подмножество элементов группы Г называется подгруппой Н, если оно удовлетворяет всем аксиомам группы.

Примеры группы:

· Совокупность всех действительных чисел без нуля образует группу, если в качестве операции взято умножение. Нейтральным элементом является 1, а обратным а^-1.

· Совокупность всех действительных чисел образует группу если в качестве операции взято обычное сложение. Нейтральным элементом является 0, а обратным элементом – этот же элемент с другим знаком.

Код называется групповым, если кодовые комбинации образуют некоторую подгруппу группы всех последовательностей длины n. Пусть, например, n=7, т.е. имеется группа семиразрядных двоичных чисел. Среди этих чисел можно выделить следующие шестнадцать, которые удовлетворяют всем аксиомам группы, т.е. образуют подгруппу:

       k  n-k     k   n-k    k   n-k                  

      0001 011    0111 010   1101 001                  

      0010 110    1000 101   1110 100              

      0011 101    1001 110   1111 111                  

      0100 111    1010 011   0000 000                  

      0101 100    1011 000                                   

      0110 001      1100 010                                   

Рассмотренный код позволяет передать шестнадцать различных сообщений. Из рассмотрения кодовых слов можно видеть, что минимальное расстояние Хемминга d_min=3, т.е. код позволяет исправлять любую одиночную ошибку.

Если передаваемые сообщения представляют собой k-разрядные двоичные числа, то групповой код всегда может быть построен таким образом, что эти сообщения будут являться первыми k символами кода, как это сделано для рассмотренного выше примера. Код, построенный таким образом, называется систематическим кодом и обозначается (n;k)-код. Первое число в скобках показывает общее число символов в коде второе – число информационных символов. Для нашего примера обозначение кода будет таким: (7;4). Оставшиеся l=n-k символов называются проверочными. В групповых кодах проверочные символы образуются путем суммирования по модулю два символов, стоящих на определенных позициях кодового слова. Поскольку операция суммирования по модулю два является линейной, то коды, образованные таким образом, называются линейными.

Линейные блоковые коды

Линейным блоковым кодом называется такой помехоустойчивый код, у которого проверочные символы формируются путем суммирования по модулю два информационных символов, расположенных на определенных позициях, а сумма двух кодовых последовательностей и произведение кодовой последовательности на элемент поля образуют также кодовые последовательности.

Основные свойства ЛБК:

1. линейность кода определяется специально выбираемой структурой кода. Линейность кода существенно упрощает процедуру кодирования и декодирования, позволяя выразить каждую кодовую последовательность в виде "линейной" комбинации небольшого числа выделенных кодовых последовательностей, так наливаемых базисных векторов;

2. сумма по модулю два двух кодовых последовательностей также является кодовой последовательностью;

3. линейный блоковый код всегда содержит кодовую последовательность, состоящую целиком из нулей;

4. если сложить по модулю два некоторую кодовую последовательность со всеми кодовыми последовательностями, то снова получится множество всех кодовых последовательностей, расположенных в другом порядке;

5. вес кодовой последовательности (W_кп) всегда должен быть > d₀;

6. вес проверочной части кодовой последовательности (W_пр.ч.кп) должен быть    всегда ≥ (do-l);

7. вес суммы по модулю два двух разрешенных кодовых последовательностей (W_åкп) должен быть всегда ≥ (d₀-l), но допускается ≥ (d₀-2);

8. групповой двоичный линейный блоковый код полностью задается как порождающей G_k,n (х), так и проверочной H_l,n (x) матрицами.