Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Префиксные коды

 

Однозначность декодирования можно обеспечить, не вводя разделительного символа, если строить код так, чтобы он удовлетворял условию, известному под названием "свойство префикса". Оно заключается в том, что ни одна комбинация более кратного кода не должна совпадать с началом ("префиксом") другого кодового слова. Коды, удовлетворяющие этому условию, называют префиксными кодами. Эти коды обеспечивают однозначное декодирование принятых кодовых слов без введения дополнительной информации для их разделения, т. е. всякая последовательность кодовых символов должна быть единственным образом разделена на кодовые слова. Коды, в которых это требование выполнимо, называются однозначно декодируемыми, или кодами без запятой.

Если код префиксный, то, читая принятую последовательность подряд с начала до конца, можно установить, где кончается одно кодовое слово и начинается следующее. Например, если код префиксный и в последовательности встретился код 110, то, очевидно, в коде не должно содержаться слов (1), (11). Закодировано префиксным кодом с а₁ = (00), а₂ = (01), а₃ = (101), а₄ = (100). На рис. 1 представлен граф (кодовое дерево) префиксного кода с сообщением а₁ = (0), а₂ = (1), а₃ = (11), а₄ = (111). Из рис. 1 следует, что если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.

 

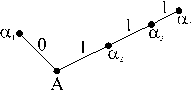
Рис. Кодовое слово непрефиксного кода

Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана.

Код Шеннона-Фано

Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.

 

Пример:

Р(а₁)=0,1 Р(а₂)=0,15 Р(а₃)=0,15 Р(а₄)=0,1 Р(а₅)=0,05

Р(а₆)=0,05 Р(а₇)=0,2 Р(а₈)=0,07 Р(а₉)=0,09 Р(а₁₀)=0,04

 

 

 

 

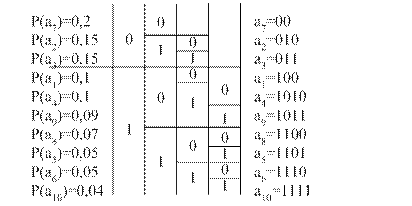
Рис.  Кодовое дерево кода Шеннона – Фано

 

Методика Шеннона – Фано не всегда приводит к однозначному построе­нию кода, поскольку при разбиении на части можно сделать больше по веро­ятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспе­чивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмечен­ных недостатков.

 

Код Хаффмана

 

Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответ­ствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последователь­ное ветвление продолжается до тех пор, пока не дойдем до вероятности каж­дой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.

Пример:

Р(а₁)=0,1 Р(а₂)=0,15 Р(а₃)=0,15 Р(а₄)=0,1 Р(а₅)=0,05

Р(а₆)=0,05 Р(а₇)=0,2 Р(а₈)=0,07 Р(а₉)=0,09 Р(а₁₀)=0,04

 

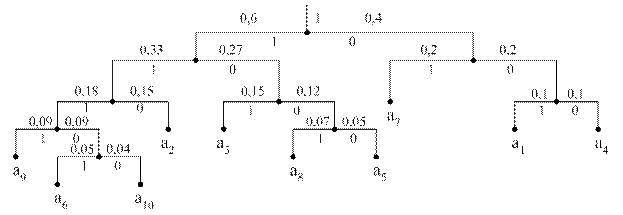
а₁=001 а₂=110 а₃=101 а₄=000 а₅=1000 а₆=11101 а₇=01 а₈=1001 а₉=1111 а₁₀=11100

 

Рис. Кодовое дерево кода Хаффмана

 

Линейные блоковые коды

 

Линейным блоковым кодом называется такой помехоустойчивый код, у которого проверочные символы формируются путем суммирования по модулю два информационных символов, расположенных на определенных позициях, а сумма двух кодовых последовательностей и произведение кодовой последовательности на элемент поля образуют также кодовые последовательности.

Основные свойства ЛБК:

1. линейность кода определяется специально выбираемой структурой кода. Линейность кода существенно упрощает процедуру кодирования и декодирования, позволяя выразить каждую кодовую последовательность в виде "линейной" комбинации небольшого числа выделенных кодовых последовательностей, так наливаемых базисных векторов;

2. сумма по модулю два двух кодовых последовательностей также является кодовой последовательностью;

3. линейный блоковый код всегда содержит кодовую последовательность, состоящую целиком из нулей;

4. если сложить по модулю два некоторую кодовую последовательность со всеми кодовыми последовательностями, то снова получится множество всех кодовых последовательностей, расположенных в другом порядке;

5. вес кодовой последовательности (W_кп) всегда должен быть > d₀;

6. вес проверочной части кодовой последовательности (W_пр.ч.кп) должен быть    всегда ≥ (do-l);

7. вес суммы по модулю два двух разрешенных кодовых последовательностей (W_åкп) должен быть всегда ≥ (d₀-l), но допускается ≥ (d₀-2);

8. групповой двоичный линейный блоковый код полностью задается как порождающей G_k,n (х), так и проверочной H_l,n (x) матрицами.

 

Задание линейных кодов с помощью порождающих и проверочных матриц

 

Линейные коды задаются с помощью порождающей G (x) и проверочной H ( x ) матриц. Эти матрицы связаны основным уравнением кодирования:

G ( x ) × H ( x ) ^T =0.

Матрица G ( x ) содержит k строк и n столбцов, ее элементами являются нули и единицы. В качестве строк матрицы G ( x ) выбираются любые ненулевые линейно независимые n-значные векторы, отстоящие друг от друга не менее чем на заданное кодовое расстояние d ₀.

Векторы v ₁, v ₂, …, v_k называются линейно независимыми, если выполняется условие

c ₁ v ₁ + c ₂ v ₂ +…+ c_k v_k = 0,

где с _i={0, 1}, а сложение выполняется по модулю два. То есть, каким бы образом мы не суммировали различные строки матрицы G ( x ), не получим суммы, равной нулю. Все множество кодовых слов состоит из строк порождающей матрицы и всевозможных комбинаций этих строк, т.е. суммы по модулю два всех строк матрицы G ( x ) сначала попарно, затем по три и так далее до суммы всех k строк.

С точки зрения алгебры все кодовые слова образуют некоторое векторное пространство, базисом которого являются строки матрицы G ( x ).

Поскольку линейно независимые векторы могут быть выбраны произвольным образом, то, очевидно, можно построить множество матриц G ( x ) с одним и тем же кодовым расстоянием d ₀.

Свойство линейной независимости векторов инвариантно относительно двух следующих операций (выполняя эти две операции, кодовое расстояние не меняется):

1) возможна произвольная перестановка строк и столбцов в матрице G ( x );

2) замена i-й строки на сумму i-й и j-й строк и т. д. (эту операцию нельзя осуществлять со столбцами матрицы G( x )).

Производя вышеуказанные операции, любую произвольную матрицу G ( x ) можно привести к так называемому приведенно -ступенчатому (каноническому) виду:

n

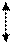
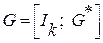
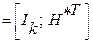k ,                              (1)

 

 

где I_k – единичная подматрица размерностью k × k ,

H^{* T} – транспонированная проверочная матрица (транспонировать – значит поменять местами строки и столбцы).

Исходя из основного уравнения кодирования, проверочная матрица имеет вид

l .

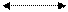
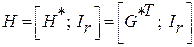                                         (2)

	n

 

 

Пример:

Возьмем порождающую матрицу кода (7,4). В этой матрице количество строк равно 4 (k=4), а количество столбцов 7(n=7).

        1 0 0 0 1 0 1                                                  

G(x)=0 1 0 0 1 1 1                                                  

        0 0 1 0 1 1 0                                                  

        0 0 0 1 0 1 1                                                  

Для того чтобы построить проверочную матрицу, необходимо транспонировать подматрицу G(x)^* и к ней приписать единичную матрицу размером l × l. Проверочная матрица будет иметь размер l×n, l = n-k=7-4=3, т.е. матрица Н(x) имеет размер 3×7. 

          1 1 1 0 1 0 0                                              

H(x)=0 1 1 1 0 1 0                                                  

          1 1 0 1 0 0 1                                                  

 

Синдромное декодирование

 

Декодирование более сложный процесс, чем кодирование.

Декодирование линейных групповых кодов основано на следующем свойстве: Проверочная H(х) и порождающая G(х) матрицы удовлетворяют соотношению G(х)*H^t(х)=0, где H^t(х) - транспонированная проверочная матрица.

Если в принятом слове F(х) отсутствуют ошибки, то матричное произведение равно нулю.

F(х)*H^t(х)= A_k(x)*G(x)*H^t(х)= A_k(x)*0=0

Ecли же при передаче информации возникли ошибки, то (F+E)*H^t=F*H^t+E*H^t=0+E*H^t=E*H^t=S – синдром, где E – вектор ошибки. Длина синдрома равна (n-k). Ненулевая величина синдрома свидетельствует о наличии ошибки. Если различным ошибкам соответствуют различные синдромы, то по виду синдрома можно определить вид ошибки и, следовательно, исправить ее.

Этапы декодирования:

1. По принятому слову

(3)

 F(x)^* вычисляется синдром S_j (х):

S_j (x)= F(x)^* × H^t(x).

2. По синдрому S_j ( x ) находится вектор ошибок E.

3. Из принятого вектора F(x)^* вычитается вектор ошибок; в результате получаем переданное слово, F(x).

Синдромный декодер состоит из схемы, вычисляющей (n-k)-разрядный синдром, дешифратора и корректирующих сумматоров по модулю два. Схема вычисления синдрома производит умножение принятого вектора на матрицу H^t(x). При отсутствии ошибок синдром равен нулю. Если синдром не равен нулю, то возбуждаются соответствующие выходы дешифратора и сигналы с ошибочных разрядов исправляются на корректирующих сумматорах.

Схема синдромного декодера кода (6, 3) представлена на рисунке.

 

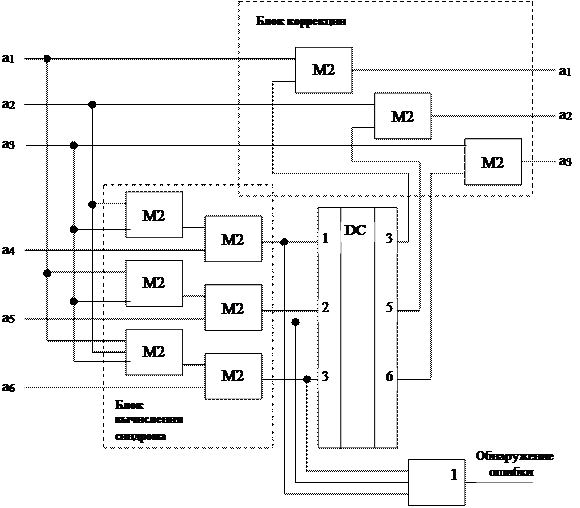Рисунок – Схема синдромного декодера кода (6, 3)

 

Пусть F(x)=111 001, например, ошибка произошла в первом разряде, т.е. принятое слово имеет вид F(x)^*=(011 001).

Вычислим синдром S_j(x)= F(x)^* × H^t(x).

       а₁а₂а₃ а₄а₅а₆

      0 1 1 1 0 0                        011

H(x) =1 0 1 0 1 0            H^t(x)= 101         S_j(x)= F(x)^* × H^t(x)=011

      1 1 1 0 0 1                        111

                                                     100

                                            010

                                            001

Синдром равен 011 (это первая строчка матрицы H^t(x), следовательно, ошибка произошла в первом разряде) и на первом выходе дешифратора должен появиться единичный сигнал, который исправит на первом корректирующем сумматоре ошибочный сигнал на противоположный – правильный. Это обеспечит получение на выходе приемника сигнала A_k(x)=111, который и передался в канал связи.

В том случае, если требуется только обнаружение ошибок, то сигналы с выхода схемы вычисления синдрома заводится на схему ИЛИ. На выходе схемы ИЛИ будет единичный сигнал в случае ненулевого синдрома, что свидетельствует о наличии ошибок в принятом сообщении.

Декодирование по синдрому применяется для коррекции ошибок малой кратности. Основная трудность при декодировании по синдрому связана с ''проблемой селектора'', который по синдрому должен однозначно установить разряды, в которых произошли ошибки, т. е. определить вектор ошибок E.

 

Мажоритарное декодирование

Способ мажоритарного декодирования привлекает как простотой описания, так и невысокой сложностью схемной реализации. Идея мажоритарного декодирования линейного кода базируется на системе проверочных равенств, а именно, в кодах с мажоритарным декодированием каждый символ может быть выражен через другие символы несколькими способами. Это позволяет для определения истинного значения символа воспользоваться принципом большинства (мажоритарным принципом).

Существует три способа построения систем проверочных уравнений при мажоритарном декодировании:

– системы с разделенными проверками;

– системы с l -связанными проверками;

– системы с квазиразделенными проверками.

В системах с разделенными проверками некоторый символ, относительно которого разделяется система уравнений, входит во все уравнения. Любой другой символ входит не более чем в одну проверку. Отсюда следует, что для коррекции t ошибок система должна состоять из (2t + 1) уравнений и иметь на столько же входов мажоритарные элементы.

Пример: Пусть имеется код (6; 3), задаваемый следующей проверочной матрицей:

                                                                    а₁а₂а₃ а₄а₅а₆

                                                              0 1 1 1 0 0

                                                   H(x) =1 0 1 0 1 0

                                                              1 1 1 0 0 1

 

Запишем систему уравнений:

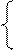а₄= a₂Åa₃

а₅= a₁Åa₃

а₆= a₁Åa₂Åa₃

 

Из этой системы можно записать систему проверочных равенств, где равенство а_i=а_i называется уравнением истинности или тривиальным.

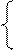 Для a₁: a₁= a₃Åa₅

             а₁ = а₂Åa₃Åa₆=а₄Åa₆

             а₁= a₁

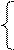Для a₂: a₂= a₃Åa₄

             а₂ = а₁Åa₃Åa₆=а₅Åa₆

             а₂= a₂

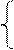Для a₃: a₃= a₂Åa₄

             а₃ = а₁Åa₅

             а₃= a₃

 

Видно, что каждый из принятых символов a_i входит в данные системы один раз, и, следовательно, если он ошибочен, то ошибочным будет одно из трех уравнений системы; два остальных – правильны. По большинству правильных проверок мажоритарный элемент принимает правильное решение об оценке состояния разряда.

С ростом числа корректируемых ошибок растет число уравнений в системе и, следовательно, увеличивается сложность мажоритарного элемента.

Декодер для кода (6,3) требует шесть сумматоров по модулю два и три мажоритарных элемента.

Схема мажоритарного декодера кода (6, 3) представлена на рисунке.

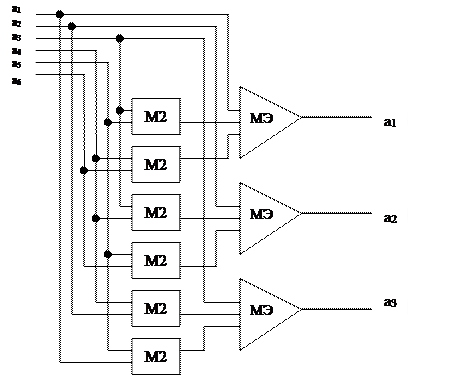
Рисунок  – Схема мажоритарного декодера кода (6, 3)

 

Достоинства мажоритарного декодирования: простота реализации, высокая скорость декодирования.

Недостатки: такие декодеры могут декодировать малый класс кодов.

 

Свойства циклических кодов

ЦК обладают всеми свойствами СЛБК, а также имеют, ряд дополнительных свойств.

К основным свойствам ЦК относятся:

1. Вес разрешенной кодовой последовательности w_кп≥d₀;

2. Вес проверочной части разрешенной кодовой по­следовательности w_пр.ч.≥d₀-1;

3. Сдвиг кодовых символов разрешенной кодовой после­довательности влево или вправо на один, два,..., ( k -1) символ вновь приводит к разрешенной кодовой последовательности. Ес­ли же при циклическом сдвиге всегда будет получатся кодовая последовательность нового кода, то такой код будет называться квазициклическим; данные коды имеют несколько большую корректирующую способность и сложность реализации, чем ЦК;

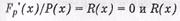4. Разрешенная кодовая последовательность без ошибок Fp'(x) при делении на полином Р(х) дает нулевой остаток ≠0 при наличии ошибок;

5. Сумма по модулю два символов двух, трех,..., (k-1) разрешенных кодовых последовательностей вновь образует разрешенную кодовую последовательность;

6. Двучлен вида х^п+1 должен делиться на порождающий полином Р(х) без остатка и результат дает проверочный полином h ( x ) =(х^п+1)/Р(х. Произведение h ( x )* P ( x )=хⁿ+1=0, а пото­му полиномы h ( x ) и Р(х) рассматривается как ортогональные и операция деления (х^п+1)/Р(х) используется в основе построения алгоритмов декодирования;;

7. Двучлен ЦК вида х^п-1 можно разложить на множители

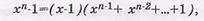
Пример:. Разложить двучлен х^п-1=х⁷-1 на множители.

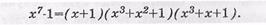Двучлен х⁷-1 раскладывается на следующие мно­гочлены:

 

Из данного выражения видно, что можно образовать шесть делителей для двучлена х⁷-1, путем комбинирования полученных трех сомножителей. Следовательно, для двучлена x ⁷ -1 существует шесть разных двоичных линейных ЦК со следующими образующими полиномами и параметрами:

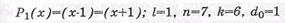 – простой код: l , k , n и t_исп ( t _исп -кратность исправленных ошибок) - измеряются в двоичных символах;

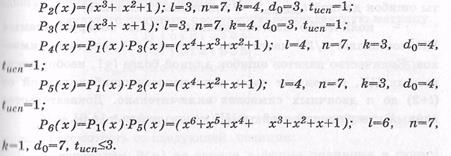
ЦК, задаваемые образующими полиномами Р₁(х), P ₂ ( x ) и Р₃(х), относятся к классу ЦК Хэмминга. ЦК, задаваемые поли­номами Р₄(х), P ₅ ( x ) и Р₆(х), являются двойственными кодами Хэ мминга и называются кодами максимальной длины.

Корректирующая способность групповых СЛБК зависит от вида (структуры) образующе­го полинома, т.е. от количества ненулевых членов данного по­линома и его максимальной степени l = n - k . В соответствии с этим можно отметить следующие свойства ЦК:

а) обнаруживающих ошибки:

- ЦК, образующий полином которого имеет более одного члена и не имеет общего множителя х, обнаруживает все одиноч­ные ошибки и любое нечетное число ошибок. Простейшим обра­зующим полиномом ЦК, обладающими данными свойствами, является полином вида Р(х)=1+х;

- ЦК, образующий полином которого имеет вид р(х)=1+х^с, обнаруживает любое нечетное число ошибок. До­казательство этого утверждения становится ясным, если обра­зующий  полином  представить  в  следующем  виде

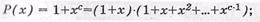
б) обнаруживающих и корректирующих ошибки: в виду того, что полином Р(х)=1+х^с нацело делится на 1+х, то согласно предыдущему свойству ЦК обеспечивает обнаружение любого нечетного количества ошибок;

- ЦК, образующий полином которого имеет максималь­ную степень l =п-к, обнаруживает любой пакет ошибок длиной 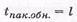 и менее двоичных символов или корректирует паке­ты ошибок длиной 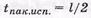двоичных символов;

- количество пакетов длиной l +1,  не обнаруживаемых ЦК, составляет 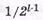части всех пакетов (l+1) двоичных симво­лов.

Количество пакетов ошибок длиной более l +1, необнаруживаемых ЦК, составляет часть всех пакетов ошибок длиной от ( l +2) до n двоичных символов включительно. 

 

Способ построения кодовых последовательно­ стей с

Многотактные фильтры

 

Многотактный фильтр – устройство состоящее из некоторого числа элементов задержки и логических элементов, связанных между собой.

Значение выходного сигнала в некоторый момент t может зависеть от значения входного сигнала в этот момент, а также от значения входных и выходных сигналов в предшествующие моменты.

Многотактный фильтр называется линейным, если отклик фильтра на сумму входных сигналов равен сумме откликов на каждый из входных сигналов в отдельности.

Многотактные фильтры являются синхронными устройствами, т.к. значения всех запоминаемых символов изменяются в один и тот же момент t, называемый тактом, т.е. фиксированный отрезок t, на который элементы задержки задерживают поступающий на вход сигнал, следовательно, выходной сигнал элемента задержки на i-ом такте совпадает с входным на (i-1) такте (предыдущем).

С помощью многотактных линейных фильтров производится:

1. вычисление остатков от деления,

2. умножение сообщения на образующий полином.

Многотактный фильтр, имеющий один вход и один выход и не имеющий цепи обратной связи, производит операцию умножения.

На рисунке приведен пример структурной схемы умножения информационного полинома (на схеме обозначен А(х)) на порождающий полином (на схеме обозначен S(х)). На рисунке а приведена схема с вынесенными сумматорами, а на рисунке б со встроенными.

 

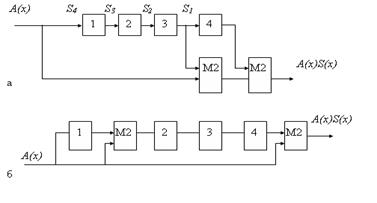
Рис. Структурные схемы для умножения полинома 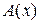 на полином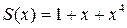

 

Многотактный фильтр, имеющий один вход и один выход, а также цепь обратной связи, выполняет операцию деления полиномов.

На рисунке приведен пример структурной схемы для деления на порождающий полином S(х). Схема для выполнения деления может быть, как и для умножения, реализована в двух вариантах: на регистрах с вынесенными сумматорами (рис. а) и встроенными сумматорами (рис. б)

 

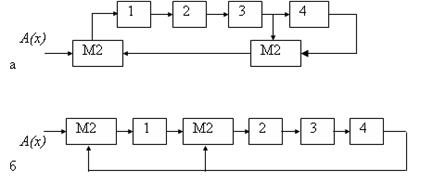
Рис. Структурные схемы для деления на многочлен S ( x )=1+ x + x ⁴

 

Задание систематических сверточных кодов

 

Систематические СК задаются:

I. с помощью порождающей матрицы – G_¥(х);

II. с помощью проверочной матрицы – H_¥(х);

III. с помощью разностных треугольников;

IV. с использованием совершенных разностных множеств.

 

I. Задание систематических СК с помощью порождающей матрицы G _¥(х)

 Порождающая матрица систематического СК имеет более сложное построение, чем у группового кода. Это определяется из-за полубесконечной структуры порождающей матрицы СК, имеющей вид:

где "0" - области матрицы, состоящие полностью из нулевых двоичных символов,

т - количество порождающих матриц вида

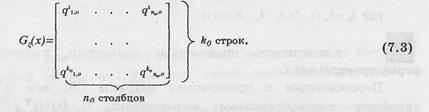
где 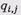– коэффициенты равны либо 1, либо 0.

 

Систематический ССК задаются следующей порождающей матрицей G _¥(х):

 

 

II. Задание систематических СК с помощью проверочной матрицы H _¥(х)

 

Проверочная матрица Н _¥ (х) СК, как и порождающая матрица, является полубес­ко­нечной:

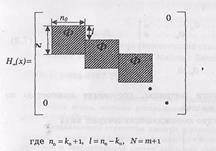
 - совокупность проверочных подматриц, имеющих форму треугольника.

Порождающая и проверочная матрицы СК, как и у линейных кодов, связаны выражением: G _¥(х) ×H^T _¥(х)= H _¥(х) ×G^T _¥(х) =0.

 Для систематического ССК с алгоритмом порогового декодирования проверочная матрица H _¥ задается следующим образом:

 

 

(n₀-k₀) строк

Из данной проверочной матрицы следует, что для ССК с 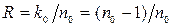 проверочная матрица Н ¥(х) содержит (n₀–k₀) строк и k₀ столбцов проверочных треугольников. Для ССК с 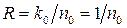, n₀= 2;3; …, проверочная матрица Н ¥(х)содержит k₀=1, т.е. один столбец и n₀ строк проверочных треугольников.

 

Каждый из проверочных треугольников Н ^D_i,_k0+i, i=1,2, …; k₀=1,2, …, проверочной матрицы Н _¥ (х)  общем случае имеет вид:

,

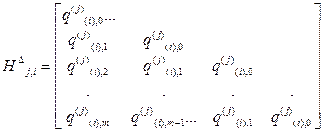где q – коэффициенты, равные либо 1, либо 0; j, i – номера соответственно строки и столбца матрицы Н_¥(х), которыми определяется проверочный треугольник; 0, …m – порядковые номера степеней, в которые возводятся соответствующие коэффициенты порождающего полинома.

Основную информацию о самоортогональных сверточных кодах ССК несут коэффициенты левого столбца и нижней строки проверочного треугольника.

Пример: задан проверочный треугольник:

 

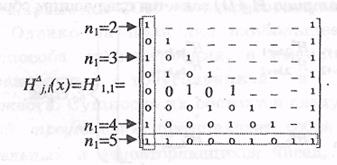
По данному проверочному треугольнику можно определить параметры ССК с алгоритмом ПД:

1. Поскольку задан один проверочный треугольник, то k₀=1, n₀=k₀+1=2,. 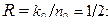 r=( n₀- k₀)/ n₀ ×100%=(1- R) ×100%=50%.

2. Так как k₀=1, то ССК задается одним порождающим полиномом, определяемым коэффициентами левого столбца и нижней строки проверочного треугольника.

g(x)=1+x²+x⁶+x⁷

3. Количество ненулевых членов порождающего полинома определяет число проверочных уравнений: J=4. Следовательно, ССК может исправлять 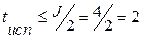 ошибки и обнаруживать  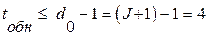ошибки.

d₀=J+1=4+1=5

4. Строки проверочного треугольника, которые начинаются с ненулевых двоичных символов, формируют проверочные уравнения, размеры данных проверок и номера позиций информационных и проверочных символов, участвующих в формировании проверочных уравнений. Размеры проверок в проверочном треугольнике обозначены цифрами перед стрелками и определяются количеством ненулевых символов в строке. Для данного примера имеем:

s₀=е₀ⁱ+e₀^p (i– информационный символ, р – проверочный)

s₂=е₀ⁱ+e₂ⁱ+e₂^p

s₆=е₀ⁱ+e₄ⁱ+e₆ⁱ+e₆^p

s₇=е₀ⁱ+e₁ⁱ+e₅ⁱ+e₇ⁱ+e₇^p

5. Длина кодового ограничения n_A и эффективная длина кодового ограничения n_e СК равны, соответственно,

n_A =(m+1)n₀=(7+1)2=16 двоичных символов;

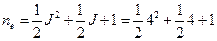=8+2+1=11 двоичных символов.

На практике наибольшее применение получили два способа построения проверочных треугольников:

- с помощью разностных треугольников

- с помощью совершенных разностных множеств.

 

III . Задание систематических СК с помощью разностных треугольников

 

Разностный треугольник представляет собой совокупность целых, действи­тель­ных и неповторяющихся чисел, записанных в форме треугольника. Для ССК с R = k₀/n₀ количество разностных треугольников равно числу k₀. Для всех разностных треугольников общим числом является “0”, который не указывается в совокупности чисел, однако учитывается при выборе степеней ненулевых членов порождающих полиномов. Степени ненулевых членов порождающих полиномов по заданным или построенным разностным тре­уголь­ни­кам можно найти путем выбора чисел:

· левого крайнего столбца разностного треугольника, считывая их сверху вниз и дополняя числом “0”,

· верхней строки разностного треугольника в такой последовательности: первое число – показатель степени второго ненулевого члена порождающего полинома; суммирование первого и второго чисел первой строки разностного треугольника определяет показатель степени третьего ненулевого члена порождающего полинома и т.д.

Пример: Определить параметры ССК с алгоритмом ПД при следующем разностном треугольнике:

 

 

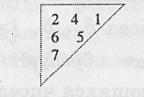
1. Так как задан один разностный треугольник, то k₀=1, n₀=k₀+1=2, 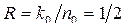, код имеет один порождающий полином.

2. Выписывая числа левого крайнего столбца разностного треугольника, определяем показатели степеней порождающего полинома: (0,2,6,7). Следо­ва­тель­но, порождающий полином ССК имеет вид: g(х)=1+x²+x⁶+x⁷. При втором способе –0; 2; 2+4=6; 2+4+1=7. Как правило, в литературе разностные треугольники табулированы и представлены, например, так: ((2,4,1), (3,5,2)). Это означает, что ССК имеет соответственно параметры: k₀=2, n₀=k₀+1=3, 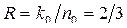и g₁(x)=1+x²+x⁶+x⁷ и g₂(x)=1+x³+x⁸+x¹⁰.

Разностный треугольник ССК может быть построен, если задан прове­роч­ный треугольник, и наоборот.

Пример: По проверочному треугольнику построить разностный.

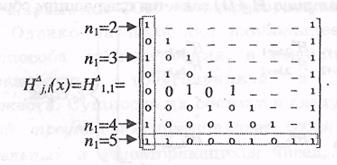
Числа крайнего левого столбца разностного треугольника определяются как результат операции вычитания порядковых номеров строк проверочного треугольника, которые начинаются с “1”. Для первого столбца получаем следующие числа: 3–1=2 (3 – номер позиции третьей строки, 1 – номер позиции первой строки); 7–1=6 и 8–1=7. Для получения чисел второго столбца за вычитаемое берем номер позиции третьей строки: 7–3=4 и 8–3=5. Для получения чисел третьего столбца за вычитаемое берем номер позиции седьмой строки: 8–7=1.

Числа, входящие в разностные треугольники, должны быть целыми, действительными и неповторяющимися. Только в этом случае будет сформирована система ортогональных (раздельных) проверок. Для получения совокупности таких чисел известно достаточно много способов их нахождения, но наиболее эффективным является способ, основанный на теории совершенных разностных множеств.

 

V. Задание систематических СК с использованием

 совершенных разностных множеств

 

Совершенное разностное множество – это совокупность целых, дей­стви­тель­ных и неповторяющихся чисел d₁, d₂, … d _x, причем d₁< d₂< d _x и разности этих чисел 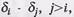 полученных по некоторому mod x ( x ¹2), также образующих совокупность целых, действительных и неповторяющихся чисел.

Данную совокупность полученных разностных чисел можно использовать в качестве исходных чисел для формирования разностных треугольников и выбора соответствующих порождающих полиномов ССК.

При выборе чисел для построения разностных треугольников необходимо выбирать числа с наименьшим их значением по номиналу, т.к. максимальное значение числа в построенных разностных треугольниках определяет максимальную степень m порождающих полиномов ССК.

Рассмотрим построение ССК с алгоритмом ПД с использованием совер­шен­ных разностных множеств.

Пусть, например, имеется совокупность b=3-х целых, действительных и неповторяющихся чисел (b=1,2,3) и эта совокупность образует b²+ b=3²+3=12 разностей по модулю b²+ b+1=3²+3+1=13, которые равны следующим числам:

1 – 0º1	12 – 8º4	2 – 8º7	0 – 3º1
3 – 1º2	0 – 8º5	8 – 0º8	1 – 3º11
3 – 0º3	8 – 2º6	8 – 12º9	0 – 1º12

Полученную совокупность разностных чисел можно разбить на следующие подмножества:

 

1	2	6	4
3	8	10	5
9	12	11	7

.

j

 

Каждый из столбцов данного множества можно использовать для построения разностного треугольника. Следовательно, можно построить k₀=4 разностных треугольника и четыре ССК с 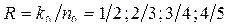, с J=4 и с 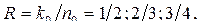с J=5, разбив данное множество на три подмножества.

 Отметим, что с использованием теории совершенных разностных множеств были рассчитаны и табулированы показатели степеней ненулевых членов порождающих полиномов ССК с 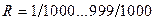  для J=2…16.

 

Структурная схема кодера

 

КРИ-1/k₀ – коммутатор распределения информации;

ФПС_кодера – формирователь проверочных символов кодера;

КОИ-n₀/1 – коммутатор объединения информации.

 

Структурная схема декодера

 

КРИ-1/k₀ – коммутатор распределения информации;

ФПС_{декодера} – формирователь проверочных символов декодера;

ФСС – формирователь символов синдрома;

АСП – анализатор синдромной последовательности;

ПЭ – пороговый элемент;

КОИ-n₀/1 – коммутатор объединения информации.

 

 

Первичные коды и эффективное кодирование

 

Первичные коды – специальный класс кодов, которые учитывают исключение избыточности информации из передаваемых сообщений с целью увеличения скорости передачи информации.

Статистическое кодирование информации (кодирование источника со­общений или сжатие информации) связано с преобразованием выходной ин­формации дискретного источника в последовательность букв заданного ко­дового алфавита. Естественно, что правила кодирования следует выбирать таким образом, чтобы с высокой вероятностью последовательность на выходе источника могла быть восстановлена по закодированной последовательности, а также, чтобы число букв кода, требуемых на одну бу­кву источника, было по возможности меньшим. В теории информации пока­зывается, что минимальное число двоичных букв кода на одну букву источ­ника, требуемых для представления выхода источника, задается энтропией источника.

Энтропия Н(А) источника сообщений А определяется как математиче­ское ожидание количества информации:

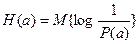,                             (1)

где Р(а) – вероятность того, что источник превышает сообщение “а” из ан­самбля А. Здесь математическое ожидание обозначает усреднение по всему ансамблю сообщений. При этом должны учитываться все вероятностные свя­зи между различными сообщениями.

Чем больше энтропия источника, тем больше степень неожиданности передаваемых им сообщений в среднем, т.е. тем более неопределенным явля­ется ожидаемое сообщение. Поэтому энтропию часто называют мерой неоп­ределенности сообщения. Можно характеризовать энтропию так же, как меру разнообразия выдаваемых источником сообщений. Если ансамбль содержит К различных сообщений, то Н(а)≤logK, причем равенство имеет место толь­ко тогда, когда все сообщения передаются равновероятно и независимо. Чис­ло К называется объемом алфавита источника.

Для двоичного источника, когда К=2, энтропия максимальна при Р(а₁)=Р(а₂) 0,5 и равна 1оg 2=1 бит. Энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объ­еме алфавита и тех же безусловных вероятностях сообщений. Для источника с объемом алфавита К=32, когда буквы выбираются равновероятно и неза­висимо друг от друга, энтропия источника Н(А)=logК=5бит. Таким источ­ником, например, является пишущая машинка русского алфавита при хаотическом порядке нажатии клавиш. Если же буквы передаются не хаотически, а составляют связный русский текст, то они оказываются неравновероятными (буква А передается чаще, чем буква Ф, и т.п.) и зависимыми (после гласных не может появиться знак "ь"; мала вероятность сочетания более трех гласных подряд и т.п.). Анализ ансамблей текстов рус­ской художественной прозы показывает, что в этом случае энтропия менее 1,5 бит на букву. Еще меньше, около 1 бит на букву, энтропия ансамбля поэтических произведений, так как в них имеются дополнительные вероятност­ные связи, обусловленные ритмом и рифмами. Если же рассматривать в качестве источника сообщений поток телеграмм, то его энтропия обычно не пре­вышает 0,8 бит на букву, поскольку тексты довольно однообразны.

 

Избыточность источника         æ 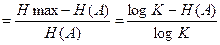                     (2)

показывает, какая доля макси­мально возможной при этом алфавите энтропии не используется источником.

 

 

С реднее число кодовых символов на одну букву источника (средняя длина сообщения):

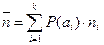, где                                            (4)

                             P(a_i) – вероятность сообщения a_i,

                             n_i – количество двоичных символов в сообщении.

Коэффициент сжатия для первичного кода ,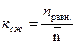  

где n_равн.= log₂К – количество двоичных символов в кодовом слове при равномерном кодировании сообщений (К – количество сообщений).

 

Префиксные коды

 

Однозначность декодирования можно обеспечить, не вводя разделительного символа, если строить код так, чтобы он удовлетворял условию, известному под названием "свойство префикса". Оно заключается в том, что ни одна комбинация более кратного кода не должна совпадать с началом ("префиксом") другого кодового слова. Коды, удовлетворяющие этому условию, называют префиксными кодами. Эти коды обеспечивают однозначное декодирование принятых кодовых слов без введения дополнительной информации для их разделения, т. е. всякая последовательность кодовых символов должна быть единственным образом разделена на кодовые слова. Коды, в которых это требование выполнимо, называются однозначно декодируемыми, или кодами без запятой.

Если код префиксный, то, читая принятую последовательность подряд с начала до конца, можно установить, где кончается одно кодовое слово и начинается следующее. Например, если код префиксный и в последовательности встретился код 110, то, очевидно, в коде не должно содержаться слов (1), (11). Закодировано префиксным кодом с а₁ = (00), а₂ = (01), а₃ = (101), а₄ = (100). На рис. 1 представлен граф (кодовое дерево) префиксного кода с сообщением а₁ = (0), а₂ = (1), а₃ = (11), а₄ = (111). Из рис. 1 следует, что если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.

 

Рис. Кодовое слово непрефиксного кода

Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана.

Код Шеннона-Фано

Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.

 

Пример:

Р(а₁)=0,1 Р(а₂)=0,15 Р(а₃)=0,15 Р(а₄)=0,1 Р(а₅)=0,05

Р(а₆)=0,05 Р(а₇)=0,2 Р(а₈)=0,07 Р(а₉)=0,09 Р(а₁₀)=0,04

 

 

 

 

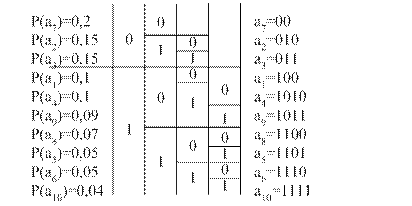
Рис.  Кодовое дерево кода Шеннона – Фано

 

Методика Шеннона – Фано не всегда приводит к однозначному построе­нию кода, поскольку при разбиении на части можно сделать больше по веро­ятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспе­чивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмечен­ных недостатков.

 

Код Хаффмана

 

Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответ­ствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последователь­ное ветвление продолжается до тех пор, пока не дойдем до вероятности каж­дой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.

Пример:

Р(а₁)=0,1 Р(а₂)=0,15 Р(а₃)=0,15 Р(а₄)=0,1 Р(а₅)=0,05

Р(а₆)=0,05 Р(а₇)=0,2 Р(а₈)=0,07 Р(а₉)=0,09 Р(а₁₀)=0,04

 

а₁=001 а₂=110 а₃=101 а₄=000 а₅=1000 а₆=11101 а₇=01 а₈=1001 а₉=1111 а₁₀=11100

 

Рис. Кодовое дерево кода Хаффмана