В ЛБК сумма по модулю два любого конечного числа разрешенных кодовых последовательностей также является разрешенной кодовой последовательностью. Поэтому, выбрав k исходных разрешенных кодовых последовательностей, которые называют базисными и суммируя их посимвольно в i различных сочетаниях, можно построить все 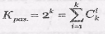 разрешенных кодовых последовательностей.
разрешенных кодовых последовательностей.
Чтобы каждое сочетание порождало новую разрешенную последовательность и чтобы в конечном итоге их общее число равнялось 2к необходимо, чтобы выполнялись следующие условия (правила):
1) исходные (базисные) кодовые последовательности должны выбираться различными;
2) нулевая кодовая последовательность (состоящая из одних 0) не должна выбираться;
3) исходные кодовые последовательности должны быть линейно-независимыми и образовывать алгебраическую группу по отношению к операции суммирования по модулю два и в том смысле они являются групповыми кодами;
4) вес (число 1) каждой исходной кодовой последовательности должен быть не менее d0 и в общем случае вес кодовой последовательности равен числу ненулевых символов;
5) вес приписываемой проверочной части строки к исходной информационной части строки должен быть не менее d0-1;
6) кодовое расстояние между любыми парами исходных кодовых последовательностей должен быть не менее d0;
7) минимальное кодовое расстояние d0 ЛБК равно наименьшему кодовому расстоянию из всей совокупности полученных кодовых расстояний (d) при попарном суммировании по модулю два двоичных символов сравниваемых последовательностей. Минимальное кодовое расстояние d0 также будет определять и минимальный вес кодовых последовательностей конкретного, т. е. проектируемого или выбираемого кода (Wmin=d0).
Задание линейных кодов с помощью порождающих и проверочных матриц
Линейные коды задаются с помощью порождающей G (x) и проверочной H ( x ) матриц. Эти матрицы связаны основным уравнением кодирования:
G ( x ) × H ( x ) T =0.
Матрица G ( x ) содержит k строк и n столбцов, ее элементами являются нули и единицы. В качестве строк матрицы G ( x ) выбираются любые ненулевые линейно независимые n-значные векторы, отстоящие друг от друга не менее чем на заданное кодовое расстояние d 0.
Векторы v 1, v 2, …, vk называются линейно независимыми, если выполняется условие
c 1 v 1 + c 2 v 2 +…+ ck vk = 0,
где с i={0, 1}, а сложение выполняется по модулю два. То есть, каким бы образом мы не суммировали различные строки матрицы G ( x ), не получим суммы, равной нулю. Все множество кодовых слов состоит из строк порождающей матрицы и всевозможных комбинаций этих строк, т.е. суммы по модулю два всех строк матрицы G ( x ) сначала попарно, затем по три и так далее до суммы всех k строк.
С точки зрения алгебры все кодовые слова образуют некоторое векторное пространство, базисом которого являются строки матрицы G ( x ).
Поскольку линейно независимые векторы могут быть выбраны произвольным образом, то, очевидно, можно построить множество матриц G ( x ) с одним и тем же кодовым расстоянием d 0.
Свойство линейной независимости векторов инвариантно относительно двух следующих операций (выполняя эти две операции, кодовое расстояние не меняется):
1) возможна произвольная перестановка строк и столбцов в матрице G ( x );
2) замена i-й строки на сумму i-й и j-й строк и т. д. (эту операцию нельзя осуществлять со столбцами матрицы G( x )).
Производя вышеуказанные операции, любую произвольную матрицу G ( x ) можно привести к так называемому приведенно -ступенчатому (каноническому) виду:
|

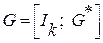
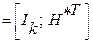 k , (1)
k , (1)
где Ik – единичная подматрица размерностью k × k ,
H* T – транспонированная проверочная матрица (транспонировать – значит поменять местами строки и столбцы).
Исходя из основного уравнения кодирования, проверочная матрица имеет вид

|
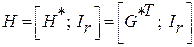 (2)
(2)
|
Пример:
Возьмем порождающую матрицу кода (7,4). В этой матрице количество строк равно 4 (k=4), а количество столбцов 7(n=7).
1 0 0 0 1 0 1
G(x)=0 1 0 0 1 1 1
0 0 1 0 1 1 0
0 0 0 1 0 1 1
Для того чтобы построить проверочную матрицу, необходимо транспонировать подматрицу G(x)* и к ней приписать единичную матрицу размером l × l. Проверочная матрица будет иметь размер l×n, l = n-k=7-4=3, т.е. матрица Н(x) имеет размер 3×7.
1 1 1 0 1 0 0
H(x)=0 1 1 1 0 1 0
1 1 0 1 0 0 1
Дата: 2018-12-28, просмотров: 857.