Основные понятия турбулентного потока: мгновенная местная скорость, пульсации скоростей и давлений, осредненные скорости и их распределение по сечению. Касательные напряжения в турбулентном потоке. Потери напора. Формула Дарси-Вейсбаха. Коэффициент гидравлического трения. Ламинарный подслой. Шероховатость стенок: абсолютная и относительная. Гидравлически гладкие и шероховатые трубы. Исследования Никурадзе. Формулы для определения коэффициента Дарси и области их применения. Определение потерь напора в трубах некруглого сечения и открытых каналах.
Указания к теме 4.4.
Турбулентное течение характеризуется беспорядочным, хаотичным движением частиц жидкости. Их скорость непрерывно меняется по величине
и направлению.
Для турбулентного течения характерны такие понятия, как "пульсация скорости","мгновенная" и "осредненная" скорости /последнюю не путать со средней скоростью/ .
Каждому моменту времени соответствует для каждой частицы своя по величине и направлению мгновенная /местная/ скорость. Изменение во времени этой скорости в данной точке жидкости и есть пульсация скорости. Несмотря на кажущуюся беспорядочность изменения мгновенных скоростей при турбулентном течении, оказывается, что они в данной точке колеблются около некоторой постоянной скорости, называемой осредненной.
Осредненные скорости в данных точках практически постоянны и направлены вдоль потока. Поэтому при турбулентном режиме движения жидкости условно можно рассматривать как параллельно-струйное, что дает возможность применять уравнение Бернулли.
Если для ламинарного течения характерны касательные напряжения вязкостного трения :
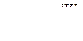 ,
,
то в турбулентном потоке появляются дополнительные напряжения - турбулентные касательные напряжения
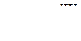
Здесь η - коэффициент турбулентной вязкости, который в отличие от коэффициента вязкости μ не может быть отнесен к категории физических констант, так как является функцией величин, меняющихся с геометрией и средней скоростью потока жидкости.
Потери напора на трение по длине трубы при турбулентном движении
определяются по формуле Дарси, однако коэффициент трения λ определяют по другим зависимостям, чем в ламинарном потоке. В общем случае λ зависит от числа Рейнольдса Re и относительной шероховатости 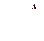 где d - диаметр трубы, а Δ - абсолютная шероховатость стенок.
где d - диаметр трубы, а Δ - абсолютная шероховатость стенок.
Характер влияния Rе и ε на сопротивление труб виден на графике Никурадзе, который получен по результатам экспериментов на трубах с искусственной paвномерной шероховатостью.
На графике можно выделить три зоны:
1.Зона гладкого сопротивления /зона гладких труб или Блазиуса/, в которой величина λ зависит только от числа Re и определяется по формуле Блазиуса:
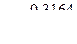
2. Переходная зона от гидравлически гладких к шероховатым трубам /зона доквадратичного сопротивления/. В этой зоне λ зависит одновременно от Re и от ε /так как в этой зоне толщина ламинарного подслоя уменьшается, вершины выступов шероховатости создают дополнительную турбулентность и сопротивления в потоке/. Для реальных труб рекомендуется формула Альтшуля:
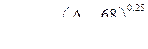
3. Зона гидравлически шероховатых труб /зона квадратичного сопротивления или автомодельная/. В этой зоне λ зависит от шероховатости ε /при больших числах Рейнольдса Rе, толщина ламинарного подслоя практически равна нулю, а каждый выступ способствует вихреобразованию/. Для этой зоны рекомендуется формула Шифринсона
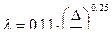
Вопросы для самопроверки.
1.Чем отличаются эпюры скоростей при ламинарном и турбулентном течениях?
2. Каково соотношение между средней и максимальной скоростями при турбулентном течении?
3. Чему равен коэффициент Кориолиса при турбулентном течении?
4. Дайте объяснение понятиям "гидравлически гладкие" и "гидравлически шероховатые" трубы. Почему одна и та же труба может быть в одном случае гидравлически гладкой, в другом - гидравлически шероховатой?
5. Объясните основные линии и зоны сопротивления на графике Никурадзе.
6. От чего зависит коэффициент сопротивления в каждой зоне? Напишите формулы для определения коэффициентов сопротивления.
7. Как связаны потери энергии со средней скоростью в каждой из зон сопротивления?
8. Почему гидравлические потери в турбулентном потоке больше, чем в ламинарном?
Литература: 1, 3
Задачи.
1. Определить потери напора на трение по длине h дл при движении воды по стальной трубе диаметром d, длиной l, со скоростью υ, кинематический коэффициент вязкости ν.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, м | 100 | 125 | 150 | 175 | 75 | 50 | 75 | 100 | 125 | 150 |
| d, мм | 100 | 150 | 200 | 100 | 150 | 200 | 100 | 150 | 200 | 100 |
| υ, м/с | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
| ν, см/с2 | 0,011 | 0,012 | 0,013 | 0,014 | 0,015 | 0,016 | 0,011 | 0,012 | 0,013 | 0,014 |
2. Определить режим движения воды в трубопроводе диаметром d при скорости течения υ; кинематический коэффициент вязкости ν.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| d, мм | 100 | 150 | 200 | 100 | 150 | 200 | 100 | 150 | 200 | 100 |
| υ, м/с | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
| ν, см/с2 | 0,011 | 0,012 | 0,013 | 0,014 | 0,015 | 0,016 | 0,011 | 0,012 | 0,013 | 0,014 |
Дата: 2018-12-28, просмотров: 506.