В общем случае движение элементарного объема жидкости является суммой поступательного, вращательного и деформационного движений. Последнее обусловлено изменением формы объема жидкости.
Учет всех этих факторов практически невозможен. Поэтому в гидравлике рассматривают в основном два вида движения — поступательное и вращательное (вихревое).
В поступательном движении, основываясь на принятом способе описания Эйлера, введем следующие понятия: линия и трубка тока, элементарная струйка.
Линия тока — линия в каждой точке которой в данный момент времени вектор скорости жидкости совпадает с касательной  (рис. 3.2, а] к этой линии.
(рис. 3.2, а] к этой линии.
В установившемся движении линия тока является траекторией частицы жидкости.
Трубка тока — поверхность, образованная линиями тока, проведенными в данный момент времени через все точки бесконечно малого замкнутого контура, нормального к линиям тока и находящегося в области, занятой жидкостью (рис. 3.2, б).
Элементарная струйка — часть движущейся жидкости, ограниченная трубкой тока (рис. 3.2, б).
Элементарная струйка обладает рядом важных свойств, которые будут использованы при дальнейших выводах: частицы жидкости не выходят из струйки и не входят в нее через боковую поверхность; это объясняется тем, что боковая поверхность струйки образована линиями тока, а следовательно, в любой точке векторы скоростей направлены по касательным; скорости частиц во всех точках одного и того же поперечного сечения струйки одинаковы, что объясняется малостью поперечного сечения;
при установившемся движении форма струйки остается неизменной во времени.
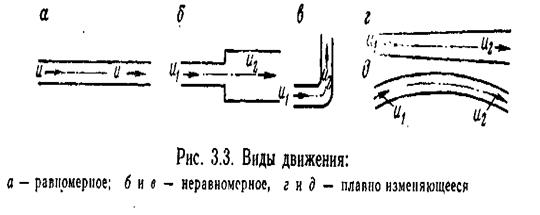
Равномерное и неравномерное движение.
В зависимости от характера изменения скорости по длине пространства, заполненного жидкостью, установившееся движение может быть: равномерным, при котором скорость по длине остается постоянной (рис. 3.3, а); неравномерным, если скорость по длине изменяется по величине и (или) направлению (рис. 3.3, б, в); плавно изменяющимся, если скорость по длине хотя и изменяется, но это изменение происходит плавно (рис. 3.3, г, д). С достаточной для практики точностью в последнем случае можно применять законы равномерного движения.
Вихревое движение.
Движению жидкости часто сопутствует вихревое движение, вызванное вращением элементарного объема. Угловая скорость вращения со элементарного объема жидкости называется вихрем, а линия, касательная во всех точках к векторам вихря 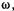 вихревой
вихревой
линией (рис. 3.4, а). Поверхность, образованная вихревыми линиями, проведенными через все точки элементарного замкнутого контура, называют вихревой трубкой, а жидкость, заключенную внутри вихревой трубки, — вихревой нитью — шнуром (рис. 3.4, б).
Расчетным вихрем является вектор угловой скорости вращения частиц относительно мгновенной оси. Физический вихрь — группа частиц, вращающихся как твердое тело вокруг некоторой мгновенной оси.
Мгновенная ось вращения может быть неподвижной или перемещающейся в пространстве. Перемещающиеся вихри наблюдаются сзади какого-либо тела, движущегося в жидкости, в виде колец дыма и пара, выходящих из труб. В природе они часто встречаются в виде смерчей. Изучение перемещающихся вихрей имеет большое значение при конструировании и исследовании лопастных машин, самолетов и при транспортировании жидкостью твердых тел.
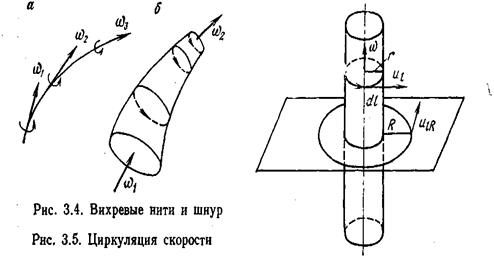
В гидромеханике широко применяется понятие циркуляции скорости — кинематической характеристики течения жидкости или газа, служащей мерой завихренности,
l Циркуляцией скорости Г вдоль замкнутого контура называется криволинейный интеграл

где  — проекция скорости на касательную к контуру;
— проекция скорости на касательную к контуру; 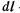 — элемент длины контура (рис. 3.5).
— элемент длины контура (рис. 3.5).
Размерность 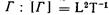 , единица в системе СИ — м2/с.
, единица в системе СИ — м2/с.
Если принять за контур окружность радиуса г, а скорость 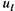 постоянной по окружности, то
постоянной по окружности, то 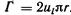 . На поверхности вихревой трубки и{ = ω*r.Тогда
. На поверхности вихревой трубки и{ = ω*r.Тогда
 |
 где F =πr2 — поперечное сечение вихревой трубки.
где F =πr2 — поперечное сечение вихревой трубки.
Циркуляция 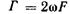 вдоль произвольного замкнутого контура, проведенного на поверхности вихревой трубки и охватывающего трубку один раз, называется интенсивностью вихря (вихревой трубки). Интенсивность вихря постоянна вдоль всей вихревой трубки.
вдоль произвольного замкнутого контура, проведенного на поверхности вихревой трубки и охватывающего трубку один раз, называется интенсивностью вихря (вихревой трубки). Интенсивность вихря постоянна вдоль всей вихревой трубки.
Можно сформулировать весьма важную теорему Гельмгольца: вихревые нити в жидкости не могут оканчиваться внезапно, они или простираются концами в бесконечность, или замыкаются в кольца, или опираются на границы жидкости, например на твердые тела.
 |
Циркуляция скорости, если пренебречь рассеиванием энергии, при удалении от вихря остается неизменной
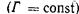 Следовательно, скорость по замкнутому контуру радиуса R (рис. 3.5), обусловленная вихрем, определится по зависимости.
Следовательно, скорость по замкнутому контуру радиуса R (рис. 3.5), обусловленная вихрем, определится по зависимости.
Виды потоков.
Поток можно представить как совокупность элементарных струек. Такое представление о потоке является струйной моделью потока.
Потоки можно разделить на напорные, безнапорные и струи.
Напорным называется поток, ограниченный со всех сторон твердыми стенками (рис. 3.6, а). Примером такого потока является движущаяся вода в водопроводе или шахтном водоотливном трубопроводе, масло в маслопроводе, движущийся воздух в выработках шахты и т. д.
Безнапорным называется поток, ограниченный твердыми стенками не со всех сторон и имеющий по всей длине свободную поверхность (рис. 3,6, б). Примером такого потока является вода в реке, водоотливной канавке шахты и т. д.
Струей называется поток жидкости, ограниченный поверхностями разрыва скоростей (ABCD на рис. 3,6, в), т. е. поверхностью в движущейся жидкости, при переходе через которую касательные к этой поверхности векторы скорости скачкообразно изменяют свою величину. Примером такого потока может служить струя воды из пожарного брандспойта или гидромонитора.
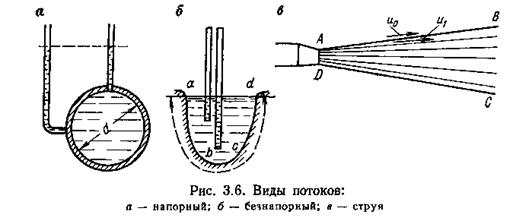
3.3.2. Живое сечение. Расход. Средняя скорость
Живое сечение ω— поверхность АВ в пределах потока (рис. 3.7, а), нормальная в каждой своей точке к проходящей через нее линии тока. При равномерном или плавно изменяющемся движении живое сечение является плоским.
Размерность 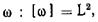 единица в системе СИ — м2.
единица в системе СИ — м2.
Периметр смачивания 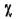 — длина контура живого сечения по твердым стенкам русла; для рис. 3,6, а
— длина контура живого сечения по твердым стенкам русла; для рис. 3,6, а 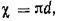 для рис. 3, 6, б — кривая abed по сечению потока.
для рис. 3, 6, б — кривая abed по сечению потока.
Размерность 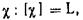 единица в системе СИ — м.
единица в системе СИ — м.
Гидравлический радиус R — отношение площади живого сечения к смоченному периметру:

Размерность R: [R] = L, единица в системе СИ – м.
Для круглого сечения (см. рис. 3.6, а)

Количество жидкости, проходящее через живое сечение в единицу времени, называется расходом.
В элементарной струйке (рис. 3.7, б) скорость одинакова во всех точках бесконечно малого живого сечения 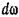 . За весьма малое время
. За весьма малое время 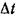 сечение ab переместится в положение
сечение ab переместится в положение 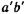 на длину
на длину 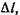 описав объем
описав объем 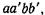 равный
равный 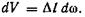
Элементарный расход
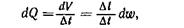
где 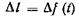 — функция, для которой существует предел отношения
— функция, для которой существует предел отношения 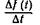 при
при 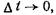 поэтому она дифференцируется по t
поэтому она дифференцируется по t
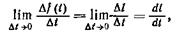
где 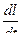 — первая производная пути по времени — скорость частиц u.
— первая производная пути по времени — скорость частиц u.
Тогда расход через живое сечение элементарной струйки будет

В разных точках живого сечения потока АВ (рис. 3.7, а) скорости различны, поэтому для установления расхода необходимо взять определенный интеграл по сечению АВ:

Размерность Q: 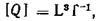 единица в системе СИ — м3/с.
единица в системе СИ — м3/с.
В выражении (3.8) расход определяет объем жидкости, проходящей в единицу времени через данное живое сечение, поэтому он называется объемным расходом.
Если перемещается жидкость переменной плотности, то удобнее определять массовый расход Qm, который выражает массу жидкости, проходящей в единицу времени через данное живое сечение
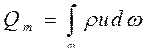 (3.9)
(3.9)
Размерность 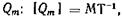 единица в системе СИ — кг/с.
единица в системе СИ — кг/с.
Аналитически интегралы (3.8) и (3.9) могут быть решены только в том случае, если известны 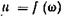 или
или 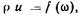 например при ламинарном движении [см. (5.17)].
например при ламинарном движении [см. (5.17)].
В других случаях этот интеграл может быть решен графически па основе экспериментальных данных. Для этого живое сечение потока разбивают на равновеликие площади 
(рис. 3.8), определяют скорость и в каждой площади Лео и расход:
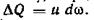
Объемный расход через живое сечение 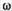 будет равен сумме расходов через намеченные площади
будет равен сумме расходов через намеченные площади
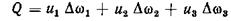
или в общем случае

Объемный расход является одним из основных параметров потока и определяет количество жидкости (газа), транспортируемой в единицу времени по трубопроводу или потребляемой различными установками. Поэтому в инженерных расчетах значение  расхода обычно является заданным. В большинстве случаев неизвестно изменение скорости по живому сечению, вследствие чего введено понятие средней скорости, которая определяется как частное от деления объемного расхода на живое сечение потока,
расхода обычно является заданным. В большинстве случаев неизвестно изменение скорости по живому сечению, вследствие чего введено понятие средней скорости, которая определяется как частное от деления объемного расхода на живое сечение потока,

Размерность v : 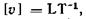 единица в системе СИ — м/с. Объемный расход может быть определен через среднюю скорость
единица в системе СИ — м/с. Объемный расход может быть определен через среднюю скорость

Соответственно массовый расход

Если известна эпюра скоростей в пределах живого сечения, то средняя скорость

Уравнение неразрывности.
Уравнение неразрывности (сплошности) является математическим выражением закона сохранения массы в гидромеханике.
В движущейся жидкости выделим параллелепипед объема dV (рис. 3.11) с бесконечно малыми ребрами dx, dy, dz.
За время dt в него входит масса 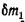 и выходит
и выходит 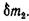 Приращение массы в направлении оси ох (рис. 3.9)
Приращение массы в направлении оси ох (рис. 3.9)
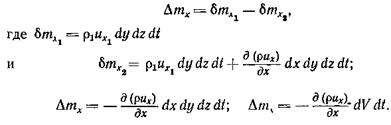
По аналогии для других осей:
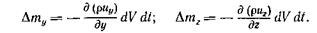
Приращение массы в параллелепипеде
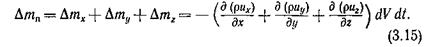
Изменение массы в объеме do за время dt может быть только за счет изменения плотности, следовательно,

Приравняем выражения (3.15) и (3.16)
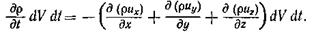
После элементарного преобразования и сокращения получим уравнение неразрывности в форме Эйлера
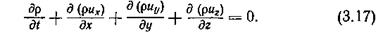
Для установившегося движения 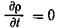 уравнение неразрывности примет вид
уравнение неразрывности примет вид
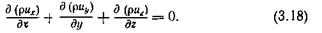
Если жидкость несжимаемая, то 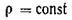 и уравнение неразрывности будет
и уравнение неразрывности будет
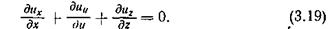
Выделим в потоке объем жидкости abdc (рис. 3.10, а) весьма малой длины, при которой можно считать живые сечения входа ас и выхода bd одинаковыми и равными ω.
Так как средняя скорость v параллельна оси х, то vx=v vy =0; vz =0. Используя уравнение (3.18), получим 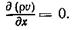
Следовательно, 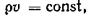 а поскольку живое сечение ω=const то произведение этих величин
а поскольку живое сечение ω=const то произведение этих величин 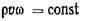 и основное условие
и основное условие


неразрывности (постоянства массового расхода) поймет вид

Если жидкость несжимаемая 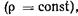 то по уравнению (3.19)
то по уравнению (3.19) 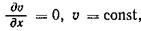 а следовательно, условие неразрывности выразится формулой
а следовательно, условие неразрывности выразится формулой

Если живое сечение потока изменяется (pис. 3.10. б), то при
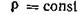
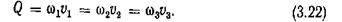
Из соотношения (3.22) ясно, что скорости изменяются обратно пропорционально живым сечениям. Если плотность изменяется по длине, то
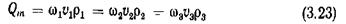
Последнее справедливо для газов, если скорость меньше скорости звука, и для капельной жидкости при отсутствии кавитации.
Уравнение Бернулли.
Основным уравнением гидродинамики является уравнение Бернулли. Для струйки идеальной жидкости оно имеет вид
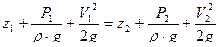 /2/
/2/
где z – геометрический напор;
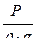 - пьезометрический напор;
- пьезометрический напор;
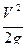 - скоростной напор.
- скоростной напор.
Все члены уравнения /2/ имеют линейную размерность. Геометрический смысл уравнения Бернулли заключается в том, что сумма всех трех напоров для идеальной жидкости есть величина постоянная и равная гидродинамическому напору. Физический смысл уравнения Бернулли заключается в том, что каждый член представляет собой удельную энергию соответственно потенциальную положения относительно Земли, потенциальную давления и кинетическую, отнесенную к единице объема. Полная удельная энергия в любом сечении струйки идеальной жидкости постоянна.
Вопросы для самопроверки к темам 3.1. и 3.2.
1. Дайте определения и укажите, чем установившееся движение
жидкости отличается от неустановившегося, равномерное от неравно
мерного, напорное от безнапорного, вихревое от потенциального. Приведите примеры этих движений.
2. Что такое линия тока, трубка тока, элементарная струйка,
вихревая линия и вихревая трубка?
3. Чем отличается линия тока от траектории частицы жидкости.
Когда они совпадают?
4. Каков геометрический смысл членов уравнения Бернулли?
Каков их энергетический смысл?
5. Как изменится кинетическая и потенциальная энергия потока
идеальной жидкости при внезапном расширении трубы?
6. Назовите причину появления вихрей в идеальной жидкости.
Литература: 1, 4.
Задачи.
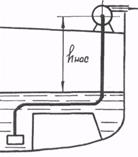
1. Найти высоту hнас установки насоса над поверхностью воды в трюме, если вакуум во всасывающем трубопроводе не превышает h м вд. ст. Известно, что производительность насоса Q , диаметр трубопровода d, суммарные гидравлические потери напора  .
.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| h, м.вд.ст. | 6 | 7 | 8 | 6 | 7 | 8 | 6 | 7 | 8 | 6 |
| Q, л/с | 50 | 60 | 40 | 30 | 40 | 50 | 60 | 50 | 30 | 40 |
| d, мм | 250 | 250 | 200 | 150 | 200 | 250 | 200 | 200 | 150 | 150 |
2. На трубопроводе диаметром d=100 мм, по которому перекачивается нефтепродукт 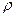 =800 кг/м3,
=800 кг/м3, 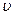 = 0,1 см 2 /с установлен вентиль. Показание дифференциального ртутного манометра h. Определить коэффициент сопротивления вентиля
= 0,1 см 2 /с установлен вентиль. Показание дифференциального ртутного манометра h. Определить коэффициент сопротивления вентиля  и вписать эквивалентную длину для него lэ, если расход Q , а труба гидравлически гладкая.
и вписать эквивалентную длину для него lэ, если расход Q , а труба гидравлически гладкая.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| h, мм | 2 | 2,5 | 3 | 2 | 2,5 | 3 | 2 | 2,5 | 3 | 2 |
| Q, л/с | 34 | 36 | 32 | 38 | 40 | 36 | 38 | 34 | 38 | 36 |
Примеры решения задач
Задача 1.
В гидравлической системе определить расход протекающей жидкости Q, при температуре t=100 при полностью открытом запорном вентиле А (ξвен=2), если давление в емкости Рм=0,48 МПа и высота уровня жидкости Н0=10 м. Материал – трубы стальные, новые. Как изменится расход жидкости Q, если вентиль А будет открыт (ξвен=4), h=6 м, d=0.1 м2, l1/2=9м, l2 =9м, L1 =16м, L2 =8м, dc=0,08м, R=0,2м, D=0.16м2
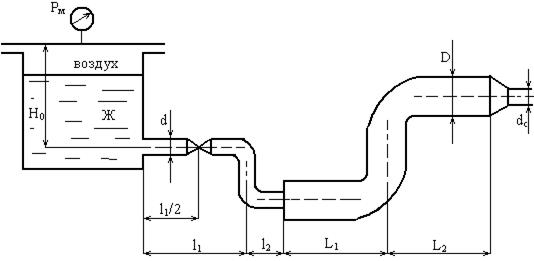
Решение.
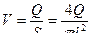 . Запишем уравнение Бернулли для заданной системы.
. Запишем уравнение Бернулли для заданной системы. 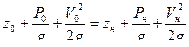 ,
, 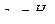 ,
,  ,
, 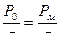 ,
, 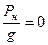 ,
, 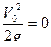 тогда
тогда 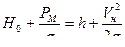 отсюда
отсюда 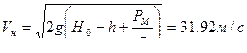 ,
, 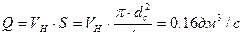 ,
, 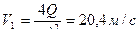 ,
, 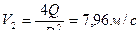 Потеря напора на входе:
Потеря напора на входе: 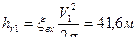 , потеря на сужение
, потеря на сужение 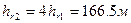 .
.
Задача 2.
Вода течет по трубе диаметром D = 20 мм, имеющая отвод (d = 8 мм). Пренебрегая потерями напора, определить расход жидкости в отводе Q, если расход в основной трубе Q = 1,2 л/с, высота H = 2м, h = 0,5 м. Режим течения считать турбулентным.
Примечание: считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъем жидкости на высоту h.
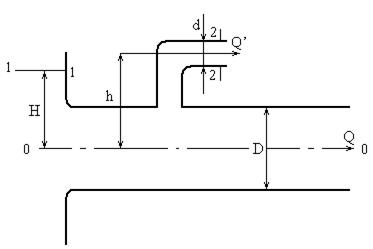
Решение.
1. Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0
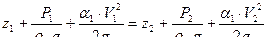
 , т.к. течение турбулентное.
, т.к. течение турбулентное.  ,
,  ,
, 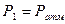 ,
, 
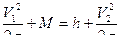
2. Определяем скорость V1
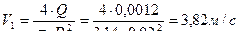 ;
; 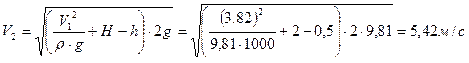
3. 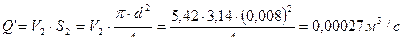
Задача 3.
Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 50 мм, если избыточное давление воздуха в баке Р0 = 16 кПа; высота уровня Н0 = 1 м; высота подъема керосина в пьезометре, открытом в атмосферу Н = 1,75 м. Потерями энергии пренебречь. Плотность керосина ρ=800 кг/м3
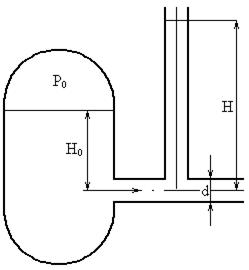
Решение.
1. 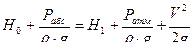 ,
, 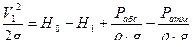 ,
,
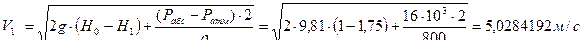
2. 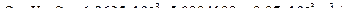
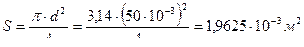
Задача 4.
Из напорного бака вода течет по трубе диаметром d1 = 20 мм и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2 = 10 мм. Избыточное давление воздуха в баке Р0’ = 0,18 МПа, высота Н = 1,6 м. Пренебрегая потерями энергии, определить скорость течения воды в трубе V1 и на выходе из насадка V2.
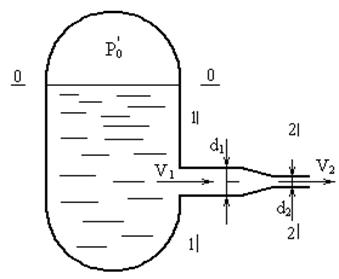
Решение.
1. Составим уравнение Бернулли для сечений 0-0 и 2-2
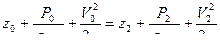
 ,
, 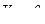 ,
, 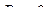 ,
,  ,
, 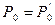 ,
, 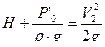 ;
; 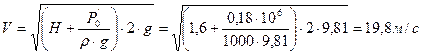
2. Расход жидкости через сечения 1-1 и 2-2 одинаковы:

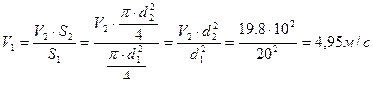
Задача 5.
Определить расход воды, выходящий из бака через короткую трубку (насадок) диаметром d = 30 мм и коэффициент сопротивления ξ = 0,5, если показание ртутного манометра hрт = 1,47 м, H1 = 1 м, H0 = 1,9 м, l = 0,1 м.
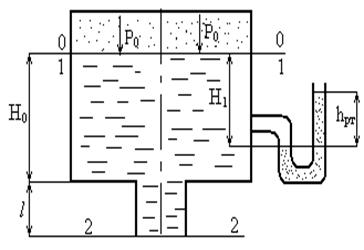
Решение.
1. Найдем давление Р0
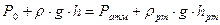 ;
;  ;
; 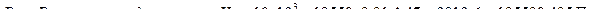
2. Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0
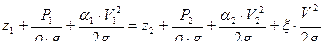
 , т.к. течение турбулентное.
, т.к. течение турбулентное.  ,
,  ,
, 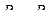 ,
, 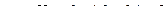 ,
,  ,
,
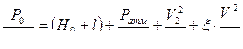 ;
; 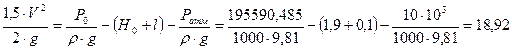
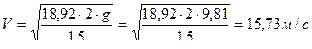 ;
; 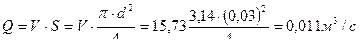
Задача 6.
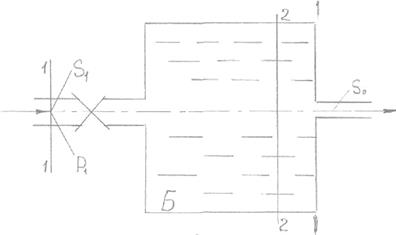
Вода под избыточным давлением Р1 = 0,3 МПа подается по трубе с площадью поперечного сечения S1 = 5 см2 к баллону Б, заполненного водой. На трубе перед баллоном установлен кран К с коэффициентом местного сопротивления ξ = 5. Из баллона Б вода вытекает в атмосферу через отверстие площадью S0 = 1 см2. Коэффициент расхода отверстия равен μ=0,63. Определить расход воды Q.
Указание: записать уравнение Бернулли для сечения 1-1 и 2-2 и основную формулу для расхода при истечении.
Решение.
Уравнение Бернулли для сечении 1-1 и 2-2 имеет вид:
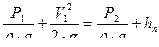 , где потери на кране К выразим как потери на местном сопротивлении согласно уравнению неразрывности расход во всех сечениях одинаковый и равен
, где потери на кране К выразим как потери на местном сопротивлении согласно уравнению неразрывности расход во всех сечениях одинаковый и равен 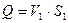 следовательно
следовательно 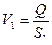 ;
; 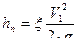
Основная формула для расхода при истечении 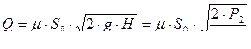 т.к. расчетный напор
т.к. расчетный напор 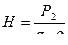 Из этого уравнения выражаем давление
Из этого уравнения выражаем давление  :
: 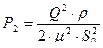
Подставим его в уравнение Бернулли и выразим в нем скорость V1 через расход, получим: 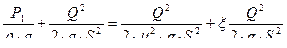 ;
; 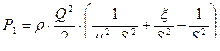 , отсюда определим расход
, отсюда определим расход
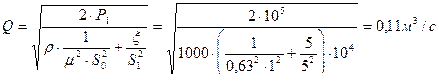
Задача 7.
Для измерения расхода воды, которая подается по трубе А в бак Б установлен водомер внутри В. Определить максимальный расход, который можно пропускать через данный расходомер при условии отсутствия в нем кавитации, если температура воды t = 600 С давление насыщенных паров соответствует hнп =2 м вод. ст. Уровень воды в баке поддерживается постоянным, равным H = 1,5 м, h = 0,5 м. Размеры расходомера d1 = 50 мм, d2= 20 мм. Атмосферное давление принять равным 760 мм.рт.ст. Коэффициент сопротивления диффузора ξдиф = 0,2
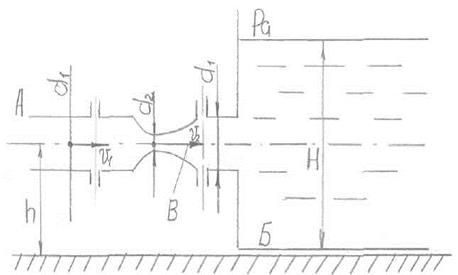
Решение.
Кавитация возникает в самом узком участке при падении давления, а нем до давления насыщенных паров (начнут образоваться пузыри насыщенного пара). Уравнение Бернулли для самого узкого участка и для точки в сосуде на уровне h имеет вид
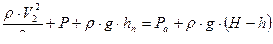
Давление образования кавитации 
Потери на диффузоре рассчитываем как потери на местном сопротивлении
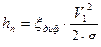
Скорости V1 и V2 связаны с уравнением неразрывности
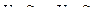 =>
=> 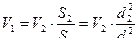
Подставим все соотношения в уравнение Бернулли
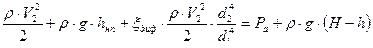
Отсюда скорость течения: 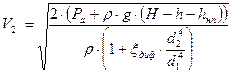
Расход равен 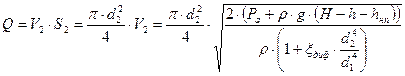
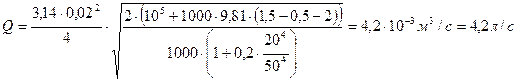
Дата: 2018-12-28, просмотров: 730.