Ламинарный и турбулентный режимы движения жидкости. Критическая скорость. Число Рейнольдса и его физический смысл.
Указания к теме 4.2.
При движении потока реальной жидкости происходят потери напора, так как часть удельной энергии потока затрачивается на преодаление различных гидравлических сопротивлений. Гидравлические сопротивления и соответственно им потери напора делятся на два режима течения жидкости. Ламинарный режим характеризуется параллельно струйным упорядоченным движением частиц жидкости, малыми расходами и скоростями режима течения. Для этого режима движения все основные закономерности могут быть установлены не только экспериментально, но и выведены аналитически. Для круглых труб значение критического числа Рейнольдса принято считать равным Reкр = 2320
Турбулентное движение жидкости, являющееся наиболее распространенным в природе и технике, представляет в то же время одно из сложнейших гидравлических явлений. Несмотря на многочисленные исследования в этой области строгая теория турбулентного режима движения до настоящего времени еще не создана, поэтому при решении практических задач наряду с использованием отдельных теорий и положений приходится широко пользоваться экспериментальными данными и эмпирическими формулами. Если скорость жидкости в трубе увеличить сверх определенного предела, то отдельные частицы жидкости будут двигаться уже не параллельно друг другу, как при ламинарном режиме, а перемешиваться в поперечном направлении. Такой вид движения называется турбулентным.
Турбулентный режим наблюдается при Re>10000. В интервале от Re>2320 до Re<10000 наблюдается так называемый переходной или неустойчивый турбулентный режим.
Число Рейнольдса Re характеризует соотношение сил инерции и трения /вязкости в потоке жидкости и определяется по формуле
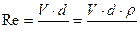
Верхняя критическая скорость – скорость, при которой происходит переход от турбулентного режима к ламинарному. Нижняя критическая скорость - наоборот.
Вопросы для самопроверки.
1. Чем отличается структура потока при ламинарном и турбулентном режимах движения?
2. Поясните физический смысл и практическое значение критерия Рейнольдса,
3. Влияет ли температура жидкости и давление в ней на число Рейнольдса?
4. Что называют критической скоростью и как ее определить?
Литература: 1, 3,4.
Примеры решения задач
Задача 1.
Определить силу прессования F, развиваемую гидравлическим прессом у которого диаметр большего плунжера D = 0,6 м, меньшего d = 0,15 м. Больший плунжер расположен выше меньшего на величину Н = 1м, рабочая жидкость – вода, температура которой 200С, усилие, приложенное к рукоятке R = 100 Н, а = 0,7 м, b = 0,08 м.
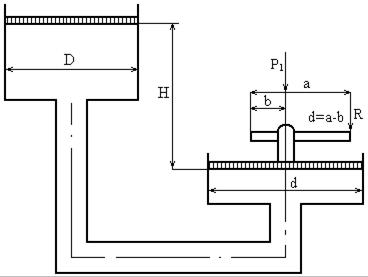
Решение.
Если к концу рукоятки насоса прилагается усилие R, то на поршень действует сила 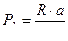 . Эта сила создает в поршне насоса давление
. Эта сила создает в поршне насоса давление 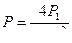 , которое, так как цилиндры соединены, в цилиндре с диаметром D создает усилие
, которое, так как цилиндры соединены, в цилиндре с диаметром D создает усилие 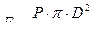 , т.е.
, т.е. 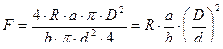
Вследствие трения в поршнях действительное усилие будет несколько меньшим, поэтому в полученную формулу вводится коэффициент полезного действия η, равный обычно 0,8 – 0,85 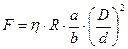
Примем η = 0,8 получим 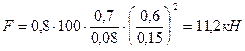
Тема 4.3. Ламинарное течение жидкости в круглых трубах.
Касательные напряжения трения при ламинарном движении жидкости. Распределение скоростей по живому сечению потока. Средняя и максимальная скорости течения. Начальный участок потока. Расход жидкости. Потери напора на трение по длине трубопровода /формула Пуазейля/. Коэффициент сопротивления трению. Определение потерянного напора /формула Дарси-Вейсбаха/. Ламинарное течение в плоских и кольцевых зазорах.
Указания к теме 4.3.
1. В настоящей главе предлагаются задачи установившегося ламинарного движения жидкости в плоских и кольцевых зазорах, а также в трубах различной формы поперечного сечения. Можно считать, что ламинарное течение в подобного рода трубопроводах и зазорах устанавливается всегда, когда число Рейнольдса 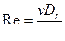 меньше критического его значения, находящегося в интервале
меньше критического его значения, находящегося в интервале 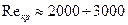 (здесь
(здесь 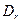 - гидравлический диаметр поперечного сечения потока;
- гидравлический диаметр поперечного сечения потока; 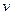 — средняя по сечению скорость).
— средняя по сечению скорость).
Метод решения задач ламинарного движения заключается в составлении дифференциального уравнения движения элемента жидкости, преобразовании этого уравнения с помощью подстановки выражения закона жидкостного трения Ньютона и интегрировании его при заданных граничных условиях задачи.
2. Простейшим случаем ламинарного движения является фрикционное безнапорное течение, вызванное перемещением бесконечно широкой пластинки по слою жидкости постоянной толщины, расположенному на неподвижной плоскости (рис. VIII—1). Определим силу трения на пластинке и расход жидкости через поперечное сечение зазора, если известно, что пластинка перемещается параллельно неподвижной плоскости с постоянной скоростью 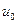 , толщина слоя b и динамическая вязкость жидкости
, толщина слоя b и динамическая вязкость жидкости 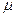 .
.
Для решения выделим в слое жидкости бесконечно малый элемент с гранями d х и dу (рис. VIII—2). Ширину грани, перпендикулярную плоскости чертежа, примем равной В. Рассмотрим, приложенные к этому элементу силы и составим уравнение его движения. К элементу в направлении оси х приложены только касательные силы трения 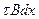 и
и 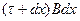 , поэтому уравнение равномерного движения имеет вид:
, поэтому уравнение равномерного движения имеет вид: 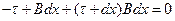 , откуда
, откуда 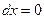 или
или 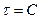 , где С— постоянная.
, где С— постоянная.
Воспользуемся теперь законом жидкостного трения Ньютона, согласно которому касательное напряжение, возникающее в слое жидкости, пропорционально угловой скорости деформации сдвига элементов этого слоя.
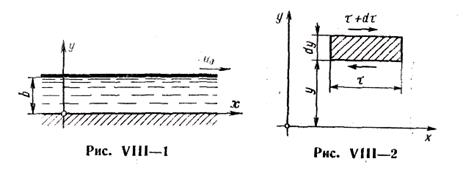
Для равномерного плоскопараллельного, движения закон Ньютона имеет вид:
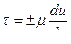 (1)
(1)
где 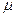 — динамическая вязкость; и — скорость движения слоя.
— динамическая вязкость; и — скорость движения слоя.
В рассматриваемом случае при выбранном направлений осей координат следует взять знак плюс ( 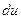 >0 при
>0 при 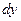 > 0), поэтому первый интеграл уравнения движения имеет вид:
> 0), поэтому первый интеграл уравнения движения имеет вид: 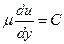 . Интегрируя вторично, получаем:
. Интегрируя вторично, получаем: 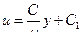 . Постоянные С и С 1 , найдем из условий на границах потока: и = 0 при у = 0; и = u 0 при у = b . Отсюда С 1 = 0 и
. Постоянные С и С 1 , найдем из условий на границах потока: и = 0 при у = 0; и = u 0 при у = b . Отсюда С 1 = 0 и 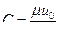 . После подстановки этих значений в интеграл получим:
. После подстановки этих значений в интеграл получим:
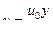 (2)
(2)
Найденный закон распределения скоростей потока по сечению зазора является линейным (рис. VIII—3). | Касательное напряжение, постоянное по сечению зазора,
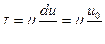 и сила трения на пластинке, площадь которой равна F :
и сила трения на пластинке, площадь которой равна F :
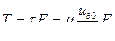 (3)
(3)
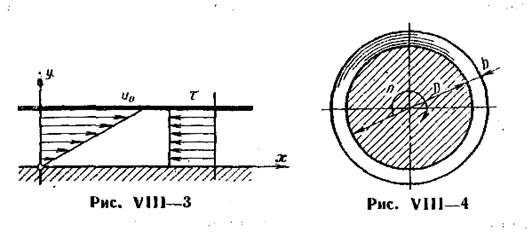
Расход жидкости через поперечное сечение зазора шириной:
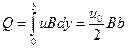 (4)
(4)
Очевидно, что средняя скорость такого фрикционного течения равна половине скорости движения пластинки, т. е. 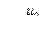 .
.
При выводе предполагалось, что температура в слое неизменна и, следовательно, вязкость жидкости постоянна.
Приведенные рассуждения позволяют вычислить момент трения на вращающемся с постоянной угловой скоростью валу (рис. VIII—4), концентрически расположенном в подшипнике с малым относительным зазором 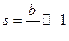 ,где b — радиальный зазор; В—диаметр вала.
,где b — радиальный зазор; В—диаметр вала.
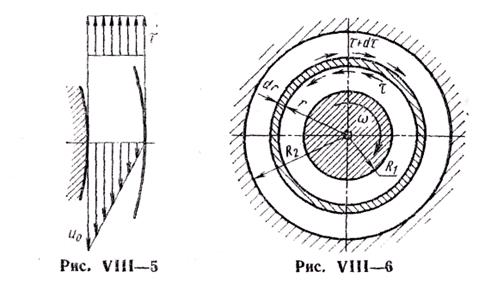
При малом относительном зазоре кривизной слоя жидкости можно пренебречь, рассматривая движение жидкости в зазоре как плоскопараллельное. Эпюры скоростей и касательных напряжений будут тогда такими, как показано на рис. VIII—5, и момент трения (формула И. П. Петрова)
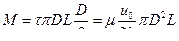 (5)
(5)
где и0 — окружная скорость вала; b—длина подшипника. Заметим, что фрикционное движение жидкости в зазоре между валом и подшипником имеет ламинарный характер для чисел Рейнольдса, определяемых неравенством 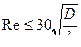 , если вращается вал, а подшипник неподвижен. В случае же вращения наружного цилиндра
, если вращается вал, а подшипник неподвижен. В случае же вращения наружного цилиндра
при неподвижном внутреннем ламинарное движение сохраняется в области чисел Рейнольдса 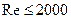 , причем число Рейнольдса определяется как
, причем число Рейнольдса определяется как
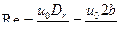
3. Если зазор между соосными цилиндрами одного порядка с диаметром одного из них, то предыдущее решение неприменимо. Рассмотрим общее решение такой задачи, определив закон распределения скоростей в зазоре и момент трения на внутреннем цилиндре, если последний расположен соосио с наружным и вращается с постоянной угловой скоростью.
Выделим кольцевой бесконечно малый элемент жидкости, размер которого в радиальном направлении равен dr , а по образующей l (рис. VIII—6).
Поскольку движение жидкости в зазоре является фрикционным, внешними силами, приложенными к выделенному кольцу, являются только касательные силы трения: 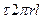 на его внутренней поверхности и
на его внутренней поверхности и 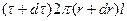 — на наружной.
— на наружной.
Составляя уравнение моментов сил трения относительно оси вращения, получаем:
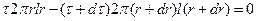
После несложных преобразований и исключения членов более высокого порядка малости последнее уравнение приводится к виду:
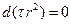 или
или 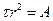 (6)
(6)
где А — постоянная.
Рассматриваемое плоское движение является криволинейным, поэтому выражение закона Ньютона (VIII—1) для жидкостного трения здесь неприменимо.

Получим выражение закона Ньютона для этого случая движения. Выделим во вращающейся жидкости два слоя на радиусах r иr + dr(рис.VIII—7) и определим скорость сдвига одного слоя относительно другого. За некоторый промежуток времени t точка А внутреннего слоя переместится в А 1 , а точка В, которую примем для простоты рассуждений лежащей на продолжении радиуса точки А, переместится в В2.
Если скорость внутреннего слоя жидкости принять равной и, и скорость наружного слоя u + du , то очевидно дуга АА 1 = ut , а дуга ВВ 1 =( u + du ) t . Следовательно, сдвиг наружного слоя относительно внутреннего
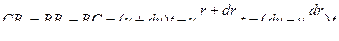 ,
,
а скорость сдвига 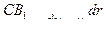 .
.
Поэтому касательное напряжение, пропорциональное угловой скорости деформации сдвига
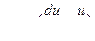 (7)
(7)
Полученное выражение представляет собой обобщенный закон Ньютона в
полярных координатах.
Подставляя в уравнение (6) выражение 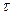 , получим линейное дифференциальное уравнение
, получим линейное дифференциальное уравнение 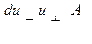 , интеграл которого
, интеграл которого 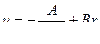 .
.
Граничные условия задачи: при 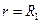
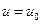 и при
и при 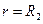
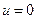 (см. рис. VIII—6), поэтому распределение скоростей
(см. рис. VIII—6), поэтому распределение скоростей
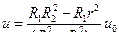 (8)
(8)
Касательное напряжение 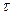 на внутреннем цилиндре
на внутреннем цилиндре
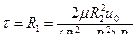 (9)
(9)
и момент трения
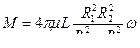 (10)
(10)
Если бы мы предположили распределение скоростей
в зазоре линейным: 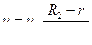 , то имели бы по формуле Петрова следующий момент трения:
, то имели бы по формуле Петрова следующий момент трения: 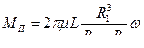 .
.
Отношение приближенного и точного выражений моментов:
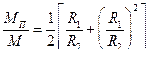
4.Рассмотрим напорное ламинарное движение жидкости в трубе круглого поперечного сечения, вызываемое перепадом давлений по длине трубы.
Выделив объем жидкости в виде горизонтального цилиндра, соосного с трубой (рис. VIII—8), и составив уравнение равновесия приложенных к нему сил, приходим к следующему дифференциальному уравнению: 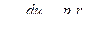 , где и — скорость жидкости на этом радиусе; р — перепад давлений на длине трубы l;
, где и — скорость жидкости на этом радиусе; р — перепад давлений на длине трубы l; 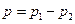 ; r — радиус выделенного цилиндра.
; r — радиус выделенного цилиндра.
Интегрируя дифференциальное уравнение, получаем закон распределения скоростей по сечению трубы:
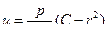

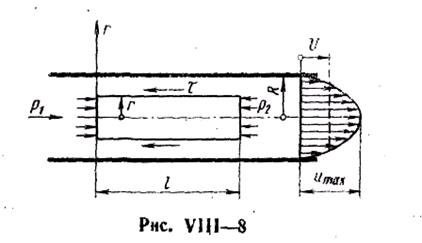
Определяя постоянную С из граничного условия, что скорость частиц жидкости на стенке равна нулю находим
(11)
где R — радиус трубы.
Скорости распределяются в поперечном сечении трубы по параболическому закону, максимум скорости имеет место на оси трубы:
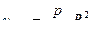 .
.
Средняя скорость v равна половине максимальной скорости:
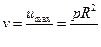
Заменяя в этом выражении R через D /2 и р через 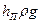 , где
, где 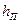 — потеря напора и
— потеря напора и 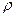 — плотность жидкости получаем:
— плотность жидкости получаем:
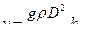
Решая это уравнение относительно 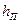 , находим выражение потерь напора при ламинарном течении в трубе:
, находим выражение потерь напора при ламинарном течении в трубе:
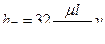 .
.
Так как 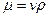 , получаем
, получаем
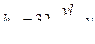 (12)
(12)
Формулу (12) можно привести к виду:
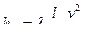 (13)
(13)
где 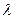 — коэффициент сопротивления трения (
— коэффициент сопротивления трения ( 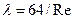 , здесь
, здесь 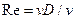 ).
).
Расход жидкости через поперечное сечение трубы (формула Пуазейля):
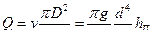 (14)
(14)
Следует заметить, что полученные выше зависимости, справедливые для стабилизированного ламинарного течения, неприменимы для входного участка трубы, где происходит формирование ламинарного потока. Длина входного начального участка ламинарного течения зависит от диаметра трубы и числа Рейнольдса и определяется выражением:
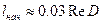 .
.
Для приближенного вычисления потерь на начальном участке можно пользоваться формулой (13), принимая 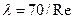 .
.
5. Более сложным случаем ламинарного движения является осевое течение жидкости под действием перепада давлений в кольцевом зазоре, образованном двумя соосно расположенными цилиндрическими поверхностями (рис. VIII—19).
Чтобы найти закон распределения скоростей по сечению зазора, выделим бесконечно малый кольцевой элемент, рассмотрим действующие на него силы и составим уравнение его движения:
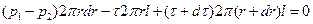 .
.
Обозначая р 1—р 2 = р и пренебрегая членом 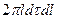 , имеющим более высокий порядок малости по сравнению с остальными членами, после несложных преобразований получаем ; следующее дифференциальное уравнение:
, имеющим более высокий порядок малости по сравнению с остальными членами, после несложных преобразований получаем ; следующее дифференциальное уравнение: 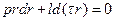 ,
,
интегрируя которое (с учетом того, что 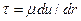 ), находим
), находим
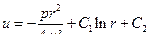
Постоянные С 1 и С2 находятся из граничных условий при 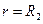
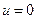 и при
и при 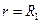 и = 0.
и = 0.
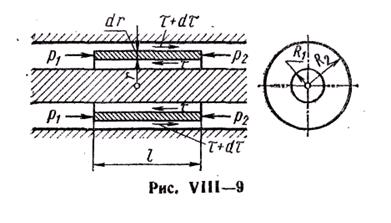
Закон распределения скоростей по поперечному сечению кольцевого зазора будет следующим:
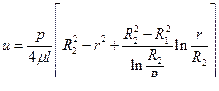 (15)
(15)
Произведя далее интегрирование скорости по сечению зазора, получим выражение для расхода жидкости:
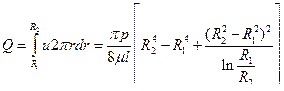 (16)
(16)
При R 1 =0 выражение (16) переходит в формулу Пуазейля для труб круглого поперечного сечения:
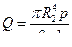
6. При решении задачи о плоском ламинарном течении в зазоре между неподвижными параллельными пластинками (рис. VIII—10) из рассмотрения равномерного движения выделенного элемента жидкости приходим к следующему дифференциальному уравнению:
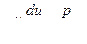 ,
,
где 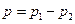 — перепад давлений на длине зазора l. Интеграл этого уравнения с учетом граничного условия (равенства нулю скорости на стенках) дает
— перепад давлений на длине зазора l. Интеграл этого уравнения с учетом граничного условия (равенства нулю скорости на стенках) дает
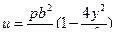 (17)
(17)
где b — зазор между пластинками.
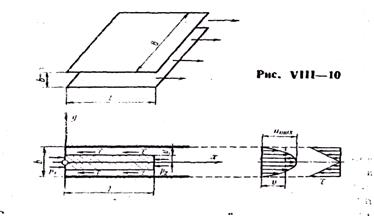
Закон распределения скоростей по высоте зазора — параболический (в пространстве — параболический цилиндр), средняя скорость
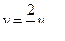 или
или 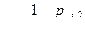
Из последней формулы легко получить выражение для расхода жидкости в зазоре между пластинками
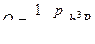 (18)
(18)
и для потери напора
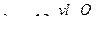 , (19)
, (19)
где В — ширина зазора.
Формулу (19) можно привести к виду
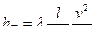 ,
,
где 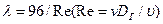 ;
; 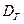 — гидравлический диаметр (
— гидравлический диаметр ( 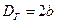 ).
).
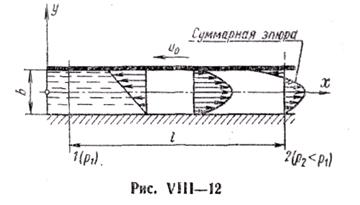
Если одна из пластинок перемещается параллельно другой с постоянной скоростью и0, то течение жидкости в зазоре будет более сложным, представляя собой сумму двух течений: фрикционного, наведенного перемещением верхней пластинки, и напорного, вызванного перепадом давлений р = р 1 — р2.
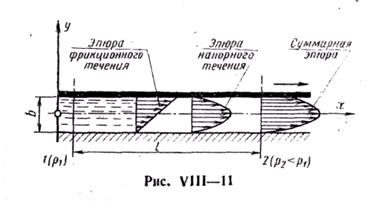
Следовательно, эпюра скоростей представляет сумму отдельных эпюр составляющих движений и имеет вид, показанный на рис. VIII—11. Ее уравнение (при расположении начала координат в середине зазора)
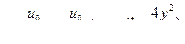 (20)
(20)
где 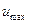 — максимальная скорость напорного течения на оси зазора.
— максимальная скорость напорного течения на оси зазора.
Имея функцию 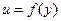 , можно легко подсчитать расход через поперечное сечение зазора и силу трения на пластинке.
, можно легко подсчитать расход через поперечное сечение зазора и силу трения на пластинке.
При перемещении пластинки со скоростью и0, т. е. в противоположном направлении (рис. VIII—12), закон изменения скоростей по сечению зазора будет иметь вид:
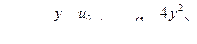 (21)
(21)
7. Полученным решением можно воспользоваться для определения утечек в зазоре между поршнем и цилиндром, если только зазор b мал по сравнению с диаметром D и если поршень расположен в цилиндре соосно.
При неподвижном поршне имеем по формуле (18) после подстановки 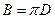
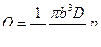 (22)
(22)
а при движущемся с постоянной скоростью 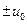
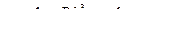 , (23)
, (23)
где знак второго слагаемого зависит от направления движения поршня.
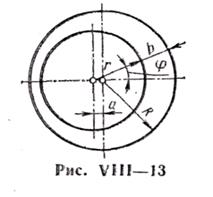
Если поршень расположен в цилиндре с некоторым эксцентриситетом (рис. VIII —13), то зазор b между ними будет величиной переменной в зависимости от угла 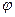 , причем при малом зазоре
, причем при малом зазоре
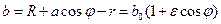 ,
,
где 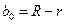 ;
; 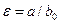 — эксцентриситет.
— эксцентриситет.
Рассматривая приближенно каждый элемент зазора, отвечающий приращению угла 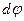 , как плоский зазор, получаем следующее значение элементарного расхода:
, как плоский зазор, получаем следующее значение элементарного расхода:
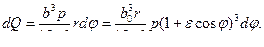
Интегрируя последнее выражение по всей окружности, находим расход в зазоре:
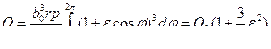 , (24)
, (24)
где 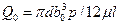 — расход в зазоре при соосном расположении поршня в цилиндре.
— расход в зазоре при соосном расположении поршня в цилиндре.
Из полученной формулы для Q следует, что при максимальном эксцентриситете, т. е. при 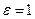 ,
,
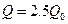
Заметим, что при турбулентном режиме расход при наибольшем эксцентриситете возрастает приблизительно в 1,2 раза по сравнению с расходом при концентричном кольцевом зазоре.
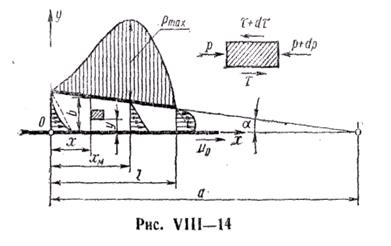
8. Рассмотрим течение в клиновом зазоре, вызванное перемещением горизонтальной плоскости относительно поверхности неподвижного башмака, который расположен по отношению к этой плоскости под небольшим углом (рис. VIII—14).
Такой случай имеет место в подшипниках и подпятниках скольжения, и поэтому рассматриваемая ниже задача разъясняет существо процесса, происходящего в смазочном слое.
Пусть угол клина равен 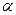 и нижняя плоскость движется вправо с постоянной скоростью и0.
и нижняя плоскость движется вправо с постоянной скоростью и0.
Определим расход жидкости в зазоре и закон распределения давления вдоль клина, предполагая поток плоскопараллельным.
Связывая оси координат с неподвижным башмаком и располагая начало координат на уровне нижней движущейся плоскости, выделим в зазоре бесконечно малый элемент жидкости и составим уравнение его движения. Пренебрегая силами инерции по сравнению с силами давления и трения, получаем:
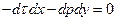 или
или 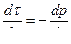 .
.
Так как при заданном направлении осей координат ( 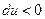 при
при 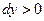 )
) 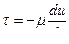 , получим
, получим 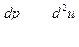 .
.
Дважды интегрируя последнее выражение, находим
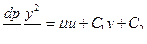
Для определения постоянных С1 и С2 используем следующие граничные условия:
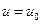 при у = 0; u =0 при у = b .
при у = 0; u =0 при у = b .
В итоге получим 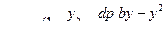
Расход жидкости в зазоре (на единицу его ширины)
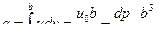 .
.
Из последнего выражения следует, что расход жидкости через поперечное сечение клина представляет сумму фрикционного расхода и расхода, обусловленного градиентом давления 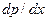 вдоль оси х. При некотором значении координаты х = хм градиент
вдоль оси х. При некотором значении координаты х = хм градиент 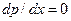 , и эпюра скоростей в этом сечении клина будет линейной. Для всех координат х < хм,
, и эпюра скоростей в этом сечении клина будет линейной. Для всех координат х < хм, 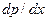 > 0, и суммарный расход жидкости равен разности расходов фрикционного и напорного течения; этому случаю соответствует левая эпюра скоростей.
> 0, и суммарный расход жидкости равен разности расходов фрикционного и напорного течения; этому случаю соответствует левая эпюра скоростей.
Для всех координат 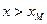 ,
, 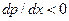 и суммарный расход будет равен сумме составляющих расходов; эпюра скоростей в поперечном сечении клина показана на рис. VIII—14 справа.
и суммарный расход будет равен сумме составляющих расходов; эпюра скоростей в поперечном сечении клина показана на рис. VIII—14 справа.
Полагая далее 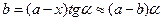 , получим следующий закон распределения давлений по длине башмака:
, получим следующий закон распределения давлений по длине башмака:
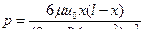 (25)
(25)
Кривая распределения давлений показана на рис. VIII —14. Исследуя полученную функцию 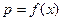 на экстремум, находим, что максимум давления имеет место при
на экстремум, находим, что максимум давления имеет место при 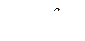 и равен
и равен

Зная закон распределения давлений, можно вычислить подъемную силу на башмаке и координату, центра давления.
8. Случай течения между параллельными пластинками можно приближенно распространить и на задачу о радиальном течении в торцовом зазоре, образованном двумя плоскими дисками (рис. VIII—15). Определим расход жидкости в зазоре, если последний равен b , а избыточное давление подводимой жидкости на внутреннем радиусе r 0 равно р0.
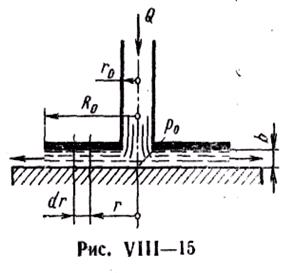
Применяя для кольцевого элемента бесконечно малой радиальной длины выведенное ранее уравнение течения между параллельными пластинками, учитывая осевую симметрию течения и пренебрегая силами инерции по сравнению с силами давления и трения, можем написать 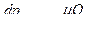 , откуда
, откуда 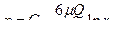
Так как при 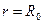 р = 0, то
р = 0, то 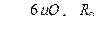 .
.
Получили закон распределения давления по радиусу зазора. Так как при 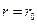 р = р0, то очевидно,
р = р0, то очевидно, 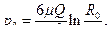 откуда искомый расход
откуда искомый расход
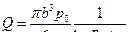 (26)
(26)
Разобранная задача встречается при расчете торцовых уплотнений машин, а также при расчете дисковых фрикционных насосов.
10. При установившемся ламинарном течении в цилиндрической трубе с некруглым поперечным сечением
задача сводится к решению дифференциального уравнения Пуассона при условии равенства нулю скорости на границе потока (частный случай дифференциального уравнения Навье — Стокса);
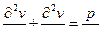
где v — скорость потока, 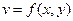 ; р — перепад давления; х, у — координаты в плоскости поперечного сечения потока;
; р — перепад давления; х, у — координаты в плоскости поперечного сечения потока; 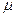 — вязкость жидкости; l — длина трубы.
— вязкость жидкости; l — длина трубы.
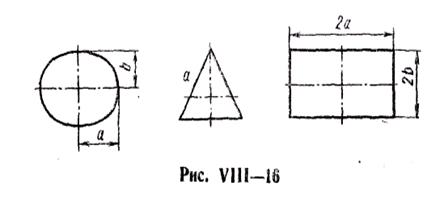
Решение задачи оказывается сложным, поэтому дадим здесь только окончательные формулы определения расхода для трех поперечных сечений (рнс. VIII—16):
а) для трубы эллиптического поперечного сечения:
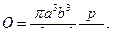 (27)
(27)
где а и b — полуоси эллипса;
б) для трубы, имеющей поперечное сечение в форме
равностороннего треугольника со стороной а,
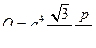 (28)
(28)
в) для трубы прямоугольного поперечного сечения
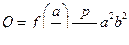 , (29)
, (29)
где 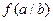 — функция, значения которой даны ниже (2а и 2 b — стороны прямоугольника):
— функция, значения которой даны ниже (2а и 2 b — стороны прямоугольника):
| a/b | 2 | 1,2 | 1,5 | 2 | 3 | 5 | 10 |
| f (a/b) | 2,25 | 2,2 | 2,08 | 1,83 | 1,4 | 0,93 | 0,5 |
Для труб некруглого сечения расчет удобно также вести по общей формуле (13): 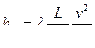 или
или 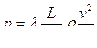 , где
, где 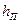 — потеря напора;
— потеря напора; 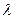 — коэффициент сопротивления трения;
— коэффициент сопротивления трения; 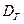 — гидравлический диаметр сечения; у — средняя скорость потока; р — потеря давления;
— гидравлический диаметр сечения; у — средняя скорость потока; р — потеря давления; 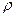 — плотность жидкости.
— плотность жидкости.
Значения 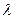 для кольцевых и прямоугольных сечений даны ниже в виде произведения
для кольцевых и прямоугольных сечений даны ниже в виде произведения 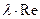 :
:
Кольцевое сечение
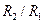
| 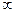
| 103 | 102 | 20 | 10 | 5 | 2,5 | 1 |
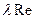
| 34 | 74,7 | 80,1 | 86,3 | 98,4 | 92,3 | 94,7 | 96 |
Прямоугольное сечение
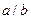
| 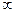
| 20 | 10 | 8 | 6 | 4 | 2 | 1 |
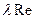
| 96 | 89,9 | 84,7 | 82,3 | 78,8 | 72,9 | 62,2 | 56,9 |
11. Вязкость жидкости изменяется при изменении давления температуры. Эти зависимости выражаются формулами 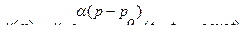 и
и 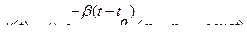 , где
, где 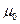 — вязкость при давлении р0 и температуре
— вязкость при давлении р0 и температуре 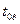 ;
; 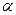 и
и 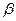 — опытные коэффициенты, различные для различных жидкостей.
— опытные коэффициенты, различные для различных жидкостей.
При одновременном учете влияния давления и температуры
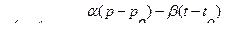 (30)
(30)
Формула (30) позволяет решать задачи ламинарного течения, в которых необходимо учитывать переменность вязкости.
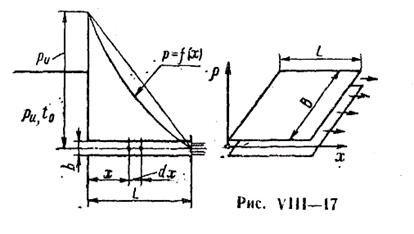
Рассмотрим, например, ламинарное течение жидкости в' зазоре между двумя параллельными пластинками (рис. VIII —17) под действием избыточного давления 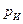 при начальной температуре
при начальной температуре 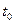 . Определим закон изменения давления вдоль зазора, а также расход жидкости через него.
. Определим закон изменения давления вдоль зазора, а также расход жидкости через него.
Так как при движении жидкости работа сил трения переходит в тепло, то между давлением и температурой жидкости в каждом сечении зазора существует определенная зависимость.
Пусть в некотором сечении х от входа избыточное давление р и температура t. Тогда, считая, что все тепло, выделяемое в результате внутреннего трения, воспринимается жидкостью и не передается стенкам, можно записать:
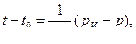
где С — удельная теплоемкость; 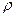 — плотность жидкости. Обозначая
— плотность жидкости. Обозначая 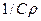 через k , получаем:
через k , получаем:
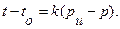
Подставляя этот результат в формулу (30) и учитывая, что на выходе давление атмосферное (р0 = 0), получаем:

или
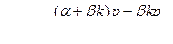
Выделив элементарный участок зазора длиной d х, можем записать по формуле (19)
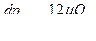
где Q — расход жидкости; В — ширина зазора; b— высота зазора.
Разделяя переменные
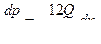
после интегрирования и несложных преобразований получаем следующий закон распределения давления по длине зазора (см. эпюру давлений на рис. VIII—17):
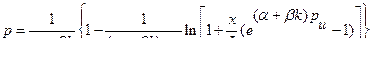
и расход
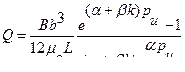
Введем обозначение 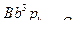 , где
, где 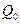 — расход через зазор, вычисленный в предположении
— расход через зазор, вычисленный в предположении 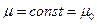 .
.
Таким образом, окончательно получим:
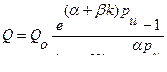 (31)
(31)
Вопросы для самопроверки.
1. Укажите закон распределения касательных напряжений при ламинарном движении.
2. Изобразите закон распределения касательных напряжений и эпюру скоростей в сечении трубопровода при ламинарном движении.
3. Каково соотношение максимальной и средней скоростями при ламинарном течении?
4. Чему равно значение коэффициента Кориолиса при ламинарном движении?
5. От каких параметров зависят потери на трение?
6. В чем состоят особенности движения жидкости на начальном участке ламинарного течения? Как определить длину этого участка и потере в нем?
7.Каковы особенности движения жидкости в плоских и цилиндрических зазорах?
Литература: 1, 2, 3
Задачи.
1. Определить расход воды, протекающей по трубопроводу в пункт А и В, если напор Н в резервуаре постоянен. Длина отдельных частей трубопровода l 1 , l 2 , l 3; диаметр d 1 = d 2 и d 3. Температура жидкости Т. Местными потерями пренебречь. Материал труб – чугун.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| H, м | 1,5 | 2,0 | 2,5 | 3,0 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 2,0 |
| l1, м | 5 | 6 | 7 | 6 | 4 | 4 | 5 | 6 | 4 | 3 |
| l2, м | 7 | 5 | 6 | 7 | 5 | 6 | 6 | 7 | 7 | 8 |
| l3, м | 8 | 8 | 5 | 6 | 4 | 3 | 4 | 5 | 6 | 7 |
| d1=d2, мм | 50 | 60 | 70 | 50 | 40 | 60 | 70 | 80 | 50 | 60 |
| d3, мм | 70 | 80 | 50 | 60 | 70 | 80 | 60 | 50 | 70 | 70 |
2.Определить высоту Н уровня воды в резервуаре, при которой в случае отбора из узловой точки А расход QA,в концевом сечении трубопровода (где давление равно атмосферному) расход будет равен QB.
Длины, диаметры и коэффициенты сопротивления трения для ветвей трубопровода приведенены в таблице данных.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| QA, л/с | 35 | 40 | 45 | 50 | 55 | 30 | 34 | 40 | 45 | 50 |
| QB, л/с | 50 | 55 | 45 | 40 | 35 | 30 | 40 | 50 | 35 | 45 |
| l1, м | 300 | 250 | 200 | 150 | 100 | 300 | 250 | 200 | 150 | 100 |
| l2, м | 150 | 200 | 250 | 300 | 100 | 150 | 200 | 250 | 300 | 150 |
| l3, м | 250 | 300 | 100 | 150 | 200 | 250 | 300 | 100 | 150 | 200 |
| l4, м | 100 | 150 | 200 | 250 | 300 | 100 | 150 | 200 | 250 | 300 |
| d1, мм | 225 | 250 | 275 | 300 | 100 | 125 | 150 | 175 | 200 | 225 |
| d2, мм | 125 | 150 | 175 | 200 | 225 | 250 | 275 | 300 | 100 | 125 |
| d3, мм | 150 | 175 | 200 | 225 | 250 | 275 | 300 | 100 | 125 | 150 |
| d4, мм | 175 | 200 | 225 | 250 | 300 | 100 | 125 | 150 | 175 | 200 |
| λ1 | 0.03 | 0.032 | 0.036 | 0.038 | 0.04 | 0.042 | 0.03 | 0.032 | 0.036 | 0.038 |
| λ2 | 0.038 | 0.04 | 0.042 | 0.03 | 0.032 | 0.036 | 0.038 | 0.04 | 0.042 | 0.03 |
| λ3 | 0.032 | 0.036 | 0.038 | 0.04 | 0.042 | 0.03 | 0.032 | 0.036 | 0.038 | 0.04 |
| λ4 | 0.042 | 0.03 | 0.032 | 0.036 | 0.038 | 0.04 | 0.042 | 0.03 | 0.032 | 0.036 |
3. Определить расход воды Q поступающей под напором Н из резервуара А в резервуар В по сифонному трубопроводу, состоящему из стальных труб диаметром d и длиной l. Какова максимально возможная высота h расположения сифона, если предельно допустимая в этом узле вакуумметрическая высота равна h вак .
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| H, м | 5 | 6 | 7 | 8 | 9 | 10 | 4 | 5 | 6 | 7 |
| l, м | 100 | 125 | 150 | 175 | 75 | 50 | 75 | 100 | 125 | 150 |
| d, мм | 100 | 150 | 200 | 100 | 150 | 200 | 100 | 150 | 200 | 100 |
| hвак, мм | 10 | 12 | 15 | 10 | 15 | 12 | 10 | 15 | 12 | 15 |
4. Из резервуара А и В с одинаковыми уровнями воды по трубам(l1, d1, l2, d2) поступающей в магистральную трубу длиной l3, d3 ,а затем сливается в резервуар С. Определить расход Q3 воды, поступающей в резервуар С при напоре Н и коэффициенте сопротивления задвижки. Принять λ1= λ3. Кроме потерь в задвижке другие потери не учитывать.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l1, м | 200 | 250 | 300 | 100 | 150 | 200 | 250 | 300 | 150 | 250 |
| l2, м | 150 | 200 | 250 | 300 | 100 | 150 | 200 | 250 | 300 | 150 |
| l3, м | 250 | 300 | 100 | 150 | 200 | 250 | 300 | 100 | 150 | 200 |
| d1, мм | 225 | 250 | 275 | 300 | 100 | 125 | 150 | 175 | 200 | 225 |
| d2, мм | 125 | 150 | 175 | 200 | 225 | 250 | 275 | 300 | 100 | 125 |
| d3, мм | 150 | 175 | 200 | 225 | 250 | 275 | 300 | 100 | 125 | 150 |
| λ1= λ3 | 0,02 | 0,025 | 0,03 | 0,025 | 0,02 | 0,03 | 0,02 | 0,025 | 0,03 | 0,02 |
| λ2 | 0,025 | 0,03 | 0,025 | 0,02 | 0,025 | 0,03 | 0,02 | 0,03 | 0,025 | 0,02 |
| ζ | 12 | 14 | 16 | 18 | 12 | 12 | 14 | 16 | 18 | 14 |
Примеры решения задач
Задача 1.
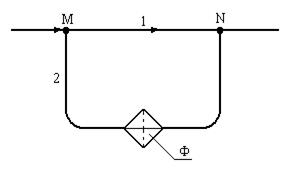
Трубопровод с расходом жидкости Q=0,32 л/с в т. М разветвляется на два трубопровода, первый размерами l 1=1.0 м, d1= 10мм, второй размерами l 2=2.0 м, d2= 8мм. В т. N эти трубопроводы сливаются. Во 2 – ом трубопроводе установлении фильтр Ф, сопротивление которого эквивалентно трубе длиной l эк=200 d2. Определить расход и потерю давления в каждом трубопроводе при ρ=900 кг/м3 и ν=1Ст= 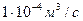 .
.
Решение.
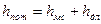 ,
, 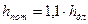
Составляем 2 функции 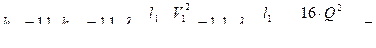

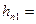
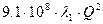
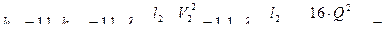
 ,
, 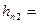
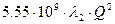
Задаемся значениями расхода (Q) от 0,1 ÷ 0,5 л/с
Составляем таблицу значений.
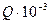 , м3/с , м3/с
| 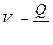 , м/с , м/с
| 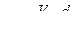
| λ1 | 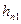 , м , м
|
| 0,1 | 1,27 | 127 | 0,5 | 4,55 |
| 0,2 | 2,55 | 255 | 0,25 | 9,1 |
| 0,3 | 3,82 | 382 | 0,16 | 13,1 |
| 0,4 | 5,09 | 509 | 0,13 | 19 |
| 0,5 | 6,37 | 637 | 0,1 | 22,75 |
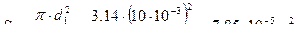 ,
, 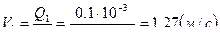
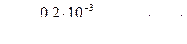 ,
, 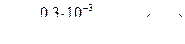 ,
, 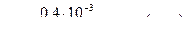 ,
,
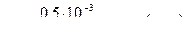 ,
, 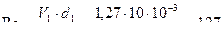 ,
, 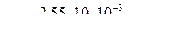 ,
,
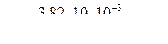 ,
, 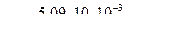 ,
, 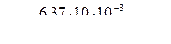
Значение числа Рейнольдса показывает нам, что течение ламинарное. Значит λ1 находится по формуле 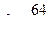 , тогда
, тогда 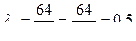 ,
,  ,
,
 ,
,  ,
, 
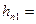
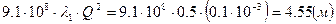 ,
,
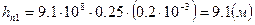 ,
, 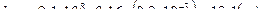 ,
,
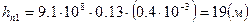 ,
, 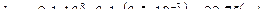
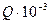 , м3/с , м3/с
| 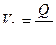 , м/с , м/с
| 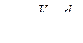
| λ2 | 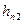 , м , м
|
| 0,1 | 2 | 160 | 0,4 | 22,4 |
| 0,2 | 4 | 320 | 0,2 | 44,8 |
| 0,3 | 6 | 480 | 0,13 | 65,5 |
| 0,4 | 8 | 640 | 0,1 | 89,6 |
| 0,5 | 10 | 800 | 0,08 | 112 |
 ,
, 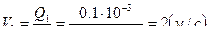
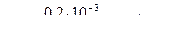 ,
, 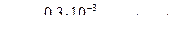 ,
, 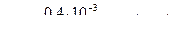 ,
,
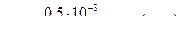 ,
, 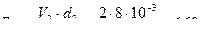 ,
,  ,
,
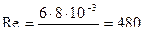 ,
, 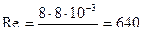 ,
, 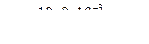
Значение числа Рейнольдса показывает нам, что течение ламинарное. Значит λ1 находится по формуле 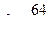 , тогда
, тогда 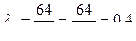 ,
, 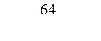 ,
, 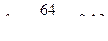 ,
, 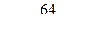 ,
, 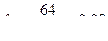
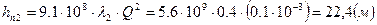 ,
,
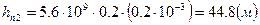 ,
, 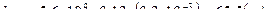
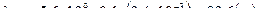 ,
, 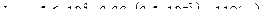
При параллельном соединений суммируется расход Q при постоянном напоре Н. Q1=0.25 л/с, Q2= 0,05 л/с, 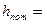 12 м.
12 м.
Задача 2.
Из резервуаров А и Б с одинаковым уровнем воды по трубам (L1 = 200 м, d1=200 мм, L2 = 100 м, d2 = 100 мм) вода поступает в магистральную трубу длиной L3 = 600 м, d3 = 200 мм, а затем сливается в резервуар С. Определить расход Q3 воды поступающей в резервуар С. Принять λ1 = λ3 = 0,02, λ2 = 0,025. Кроме потерь в задвижке другие местные потери напора не учитывать.
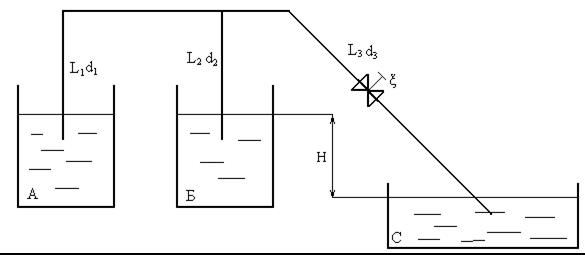
Решение.
Запишем потери для каждой ветви трубопровода: для ветви 1 и 2 будут только потери по длине, для 3 еще и местные сопротивления
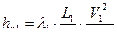 ;
; 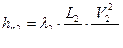 ;
; 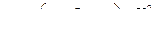
Из уравнения расхода 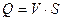 выразим
выразим 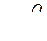 получим
получим
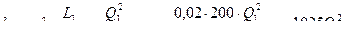
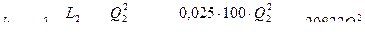
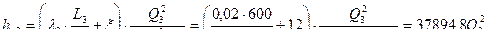
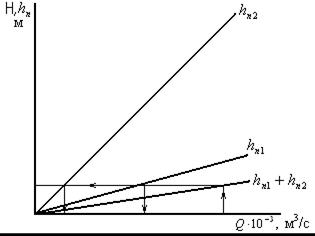
| Q | 0,004 | 0,008 | 0,012 | 0,016 | 0,02 |
| hn1 | 0,017 | 0,066 | 0,15 | 0,26 | 0,41 |
| hn2 | 0,33 | 1,33 | 2,9 | 5,3 | 8,3 |
| hn3 | 0,6 | 2,4 | 5,4 | 9,7 | 15,1 |
Из графика получим расход Q3 = 0,02048 л/
Дата: 2018-12-28, просмотров: 703.