Тема 4.1. Динамика реальной жидкости.
Уравнения Бернулли для струйки и потока реальной жидкости. Их геометрическое и энергетическое толкование. Коэффициент Кориолиса. Общие сведения о гидравлических потерях напора. Потери напора в судовых системах и особенности их определения. Примеры практического использования уравнения Бернулли: трубка Пито - Прандтля, расходомер Вентури.
Указания к теме 4.1.
Уравнение Бернулли для струйки реальной жидкости имеет вид
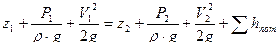
Уравнение Бернулли для сечений потока реальной жидкости имеет вид
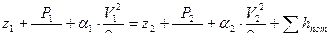
где α - коэффициент Кориолиса /учитывает неравномерность распределения скоростей по сечению и представляет собой отношение действительной кинетической энергии потока к энергии, вычисленной по средней скорости;
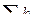 - сумма гидравлических потерь напора /потерь энергии/ между сечениями.
- сумма гидравлических потерь напора /потерь энергии/ между сечениями.
Все члены данного уравнения имеют тот же смысл, что и в уравнении для идеальной жидкости, однако уравнение для реальной жидкости, в отличии от уравнения для идеальной жидкости, представляет собой не закон сохранения энергии, а баланс энергии.
Гидравлические потери бывают двух типов: потери по длине и в местных сопротивлениях.
Потерями по длине называются потери обусловленные трением жидкости о стенки трубопровода.
Местными сопротивлениями называются сопротивления движению жидкости, обусловленные конструктивными элементам трубопроводов, вызывающими резкую деформацию потока.
Вопросы для самопроверки.
1. Дайте определение средней скорости потока реальной жидкости.
2. В чем заключается Физический смысл коэффициента α?
3. Что такое расход? Укажите способы определения расхода.
4. Чем отличаются уравнения Бернулли для идеальной и реальной
жидкости, для элементарной струйки и потока?
5. В каком случае пьезометрическая и напорная линии параллельны? Когда они по ходу движения сближаются или удаляются?
6. Почему гидравлический уклон потока реальной жидкости всегда положителен?
Литература: 1, 3
Задачи.
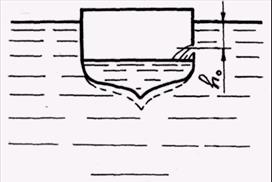
1. Судно получило пробоину (диаметр отверстия d = 25 см), находящуюся ниже ватерлинии на глубине h0 /рис.20/ . Для потери плавучести судна достаточно принять 6 тонн воды. Площадь затопления трюма S = 1500 м2. Через какое время t судно потонет, если коэффициент расхода μ.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| h0, м | 3 | 4 | 5 | 3,5 | 4,5 | 5,5 | 3 | 4 | 5 | 6 |
| 6, т | 900 | 1000 | 1100 | 1200 | 900 | 1000 | 1000 | 1100 | 900 | 1200 |
| μ | 0,61 | 0,6 | 0,62 | 0,62 | 0,61 | 0,60 | 0,60 | 0,20 | 061 | 0,61 |
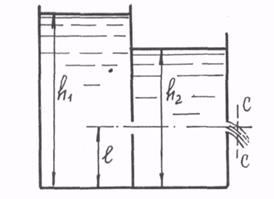
2. В вертикальной стенке, разделяющей резервуар на два отсека, имеющей круглое отверстие диаметром d1=5 см, происходит истечение жидкости. Уровень воды в левом отсеке резервуара поддерживается постоянным (h1= const), расход через отверстие Q. Определить глубину h2 воды в правом отсеке и диаметр d2 отверстия в наружной стенке, а также скорость струи в сжатом сечении С-С. Центры
отверстий расположены на высоте l=1 м от дна. Решить задачу из предположения, что отверстия малые, с совершенным сжатием струи.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Q, л/с | 3,0 | 3,1 | 3,2 | 2,5 | 2,6 | 2,7 | 2,8 | 3,0 | 3,2 | 3,6 |
| h1, м | 2,4 | 2,5 | 2,7 | 2,0 | 2,2 | 2,4 | 2,5 | 2,6 | 2,8 | 2,5 |
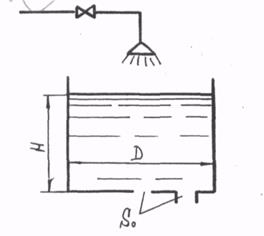
3. Цилиндрический бак диаметром D=1 м имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком. Определить:
а) какой диаметр должны иметь отверстия, чтобы при поступлении в бак воды в количестве Q уровень поддерживался на высоте Н;
б) за какое время t произойдет опорожнение бака через цилиндрический насадок после прекращения притока воды
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Q, л/с | 28 | 30 | 32 | 26 | 24 | 30 | 28 | 32 | 30 | 281,0 |
| H, м | 1,0 | 1,2 | 1,4 | 1,0 | 1,0 | 1,4 | 1,2 | 1,5 | 1,0 | 1,3 |
Примеры решения задач
Задача 1.
Определить без учета местных сопротивлений напор для обеспечения пропуска расхода масла в количестве Q=0,5 л/с по трубопроводу постоянного сечения d= 25мм длиной l=75 м. Кинематический коэффициент вязкости ν= 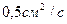 .
.
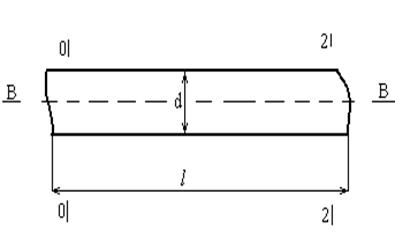
Решение.
Составляем уравнение Бернулли для сечения 00 и 22 относительно плоскости ВВ.
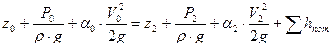 после преобразований получим
после преобразований получим 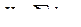 ,
,
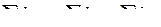 где
где 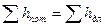 ,
, 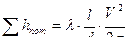 , Q=VS, где
, Q=VS, где
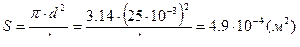 ,
, 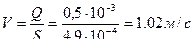 ,
,
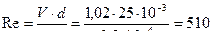 Значение числа Рейнольдса показывает нам, что течение ламинарное.
Значение числа Рейнольдса показывает нам, что течение ламинарное. 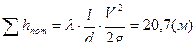
Задача 2.
При истечении из резервуара в атмосферу по горизонтальной трубе d=300мм и длиной 2l = 92 м, уровень воды в пьезометре, установлен на середине длины трубы, hn = 4,5 м. Определить расход Q и коэффициент гидравлического трения трубы λ, если статический напор в баке постоянен и равен H= 10м. Сопротивлениями воды в трубе пренебречь.
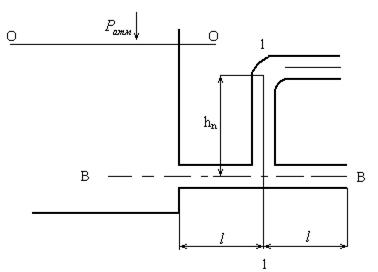
Решение.
Составляем уравнение Бернулли для сечений 0-0 и 1-1 относительно оси В-В
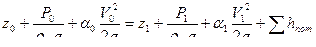 ,
, 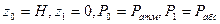 , V0=0 и V1= ?
, V0=0 и V1= ?
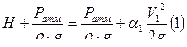 , так как режим турбулентный, то α=1
, так как режим турбулентный, то α=1
Найдем Рабс из формулы пьезометрической высоты 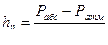
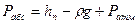 , подставляем
, подставляем 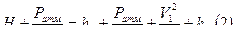 ,
, 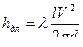 , абсолютная шероховатость труб Δ = 0,05 мм,
, абсолютная шероховатость труб Δ = 0,05 мм, 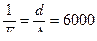 , по таблице находим λ = 0,013, подставив потери в формулу 2 найдем скорость.
, по таблице находим λ = 0,013, подставив потери в формулу 2 найдем скорость. 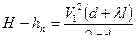 ,
, 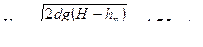 , находим расход Q=VS,
, находим расход Q=VS, 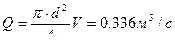
Задача 3.
Определить расход в трубе с краном, если длина трубы l = 30 м, d=200мм, высота воды в напорном баке H= 4м, λ=0,03.
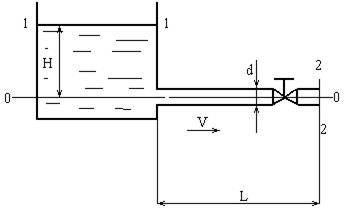
Решение.
Записываем уравнения Бернулли для сечения 1-1 и 2-2 относительно 0-0: 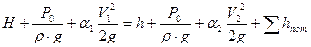 , так как диаметр трубы << диаметра напорного бака, то скоростью убывания жидкости в баке V1 можно пренебречь. Коэффициент Кориолиса α2=1 получаем
, так как диаметр трубы << диаметра напорного бака, то скоростью убывания жидкости в баке V1 можно пренебречь. Коэффициент Кориолиса α2=1 получаем 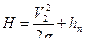 , где V2 – скорость на выходе из трубы. Потери складываются из потерь по длине и по местным сопротивлениям. Потери по местным сопротивлением состоят из потерь на выходе и на кране.
, где V2 – скорость на выходе из трубы. Потери складываются из потерь по длине и по местным сопротивлениям. Потери по местным сопротивлением состоят из потерь на выходе и на кране. 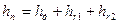 , потери по длине
, потери по длине 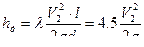 , местные потери на выходе: ξ1=0,5 (определяем по таблице)
, местные потери на выходе: ξ1=0,5 (определяем по таблице) 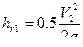 , местные потери на кране ξ2=5,
, местные потери на кране ξ2=5, 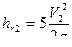 ,
, 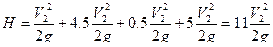 =>
=> 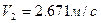 расход определяется по формуле Q=V2S2,
расход определяется по формуле Q=V2S2, 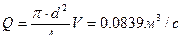 .
.
Задача 4.
Определить расход жидкости, вытекающей из трубы диаметром d=16 мм через плавное расширение (диффузор) и далее по трубе диаметром D=20мм в бак. Коэффициент сопротивления диффузора ξ = 0,2 (отнесен к скорости в трубе), показание манометра Рм = 20 кПа, высота h = 0,5 м, Н=5м. Плотность жидкости ρ=1000 кг/м3. Учесть потери на внезапное расширение, потери на трение пренебречь, режим течения считать турбулентным.
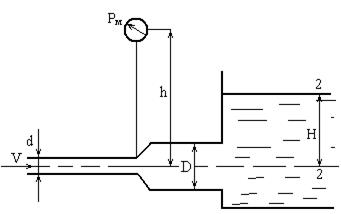
Решение.
1. Составим уравнение Бернулли относительно сечений 1-1 и 2-2
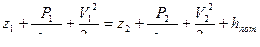
где 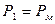 ;
;  ;
; 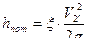 ;
;  ;
; 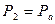 ;
; 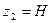 ;
; 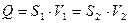 ;
; 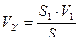
Получим: 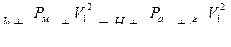 ;
; 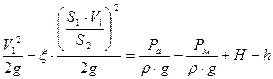
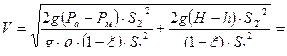
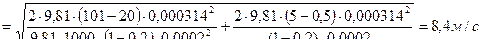
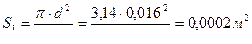
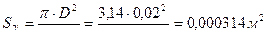
2. Определяем расход Q:
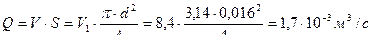
Задача 5.
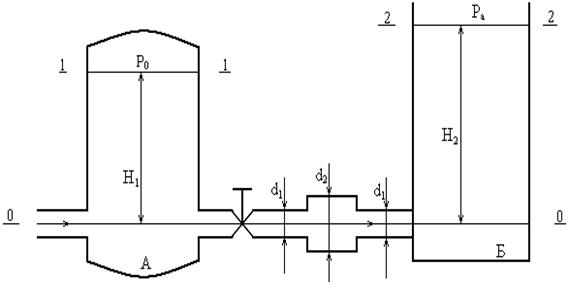
Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления ξв = 3 по трубе. Размеры: d1 = 40мм = 0,04 м,
d2 = 60 мм = 0,06 м, H1=1 м, H2=2 м. Избыточное давление в напорном баке Р0=0,15МПа. Считаем режим течения турбулентным и, пренебрегая потерями напора на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях.
Решение.
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0
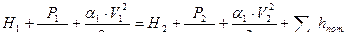
Т.к. площади резервуаров значительно больше площадей трубопроводов, то скоростями V1 и V2 пренебрегаем. P1=Рм, а Р2=Ра, то Р2 как манометрическое давление равно нулю, поэтому:
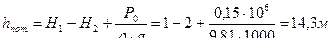
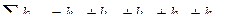
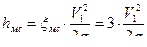 ;
; 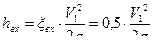 , где
, где 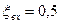 - по справочнику
- по справочнику
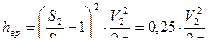 ;
; 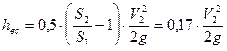
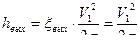 , где
, где 
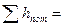
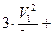
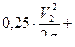
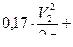
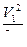
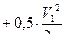 ;
; 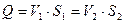 ;
; 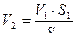
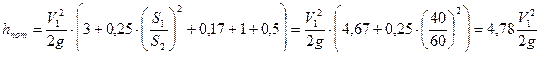
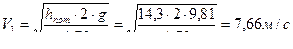
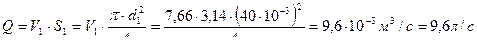
Задача 6.
К расходомеру присоединены два пьезометра и дифференциальный манометр. Выразить расход воды Q через размеры D и d, разность показания пьезометров ΔH, а также через показания манометра Δh. Дан коэффициент сопротивления ξ участка между сечениями 1-1 и 2-2.
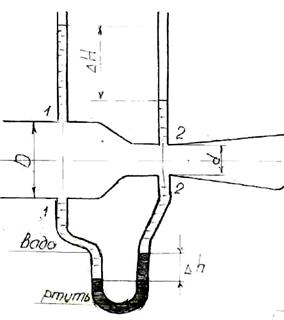
Решение.
Составим уравнение Бернулли:
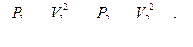
Уравнения расхода 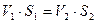
 - потеря напора м/у сечениями 1-1 и 2-2
- потеря напора м/у сечениями 1-1 и 2-2
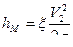 ;
; 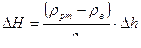 ;
; 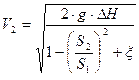 ;
; 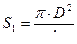 ;
; 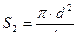
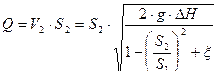
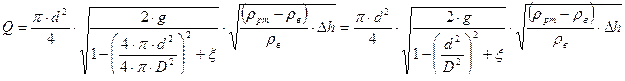
Задача 7.
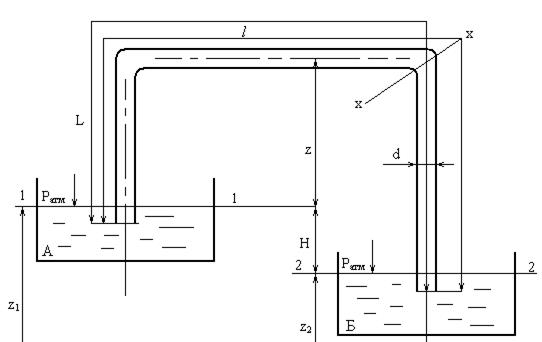
По сифону (d = 100 мм, l= 20 м) вода с расходом Q = 10 л/с переливается из резервуара А и Б. Определить разность горизонтов воды в резервуарах и величину наибольшего вакуума в сифоне. Расстояние от уровня воды в резервуаре А до центра сечения х-х равно z = 3 м, расстояние от начала сифона до сечения х-х равно l = 15 м. Коэффициент шероховатости старых стальных труб сифона n = 0,0125 мм, ν = 0,0131 см2/с
Решение.
Определить скорость и режим движения жидкости:
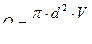 ;
; 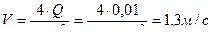 ;
; 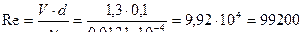 - турбулентный
- турбулентный
Составляем уравнение Бернулли для сечений 1-1 и 2-2
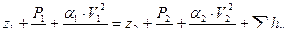
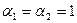 , т.к. течение турбулентное.
, т.к. течение турбулентное. 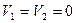 ,
, 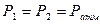 ,
, 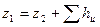 ,
, 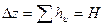 .
.
Определим разность горизонтов
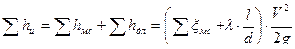 ;
; 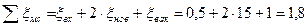
Воспользовавшись графиком определим: λ= 0,0451 (квадратичная зона)
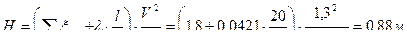 ;
;
Определим величину наибольшего вакуума в сифоне:
Составим уравнение Бернулли для сечении 1-1 и х-х
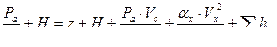 ;
; 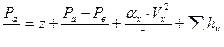
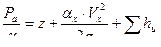 ;
;  ;
; 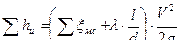
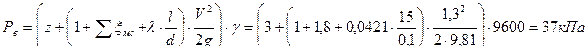
Вывод: Разность горизонтов воды в резервуарах 0,88 м, а величина наибольшего вакуума в сифоне 37 кПа.
Задача 8.
Вода перетекает из верхнего резервуара в нижний по расширяющейся трубе – диффузору, имеющему угол конусности и плавно закругленный выход. Пренебрегая потерей напора на входе в диффузор, определить при каком уровне воды Н1 в верхнем резервуаре абсолютное давление в узком сечении 1-1 диффузора сделается равным нулю. Коэффициент сопротивления диффузора ξдиф =0,2. Размеры: d1 = 100мм = 0,1 м, d2 = 150 мм = 0,15 м, H2=1,15 м. Плотность воды ρ = 1000 кг/м3. Учесть потерю на внезапное расширение при выходе из диффузора. Pа = 750 мм. рт. ст. = 99,7 кПа.
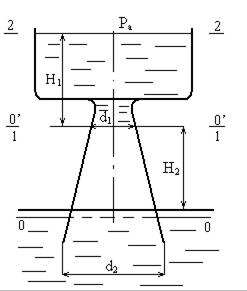
Решение.
Из выражения расходов выражаем V1 через V2
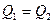 ;
; 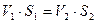 ;
; 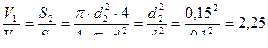 ;
; 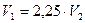 ;
;
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0
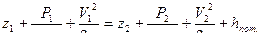 ;
; 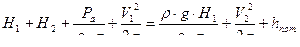 ;
; 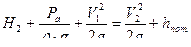
Составим уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0’-0’
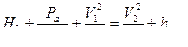 ;
; 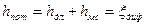
Вычисляем исходную величину 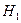 :
: 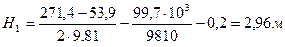
Задача 9.
Вода подается в открытый верхний бак по вертикальной трубе длиной l1=6 м и диаметром d= 50мм за счет движения воздуха в нижнем замкнутом резервуаре. Определить давление Р воздуха, при котором расход будет равен Q=4 л/с. Принять коэффициент сопротивления: вентиля ξв=8, входа в трубу ξвх=0,5, входа в бак ξвых=1,0. Эквивалентная шероховатость стенок трубы kэ=0,2 мм.
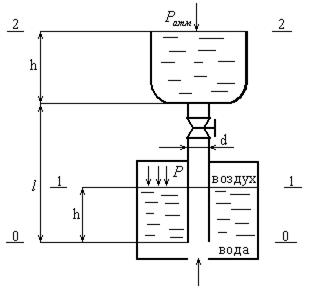
Решение.
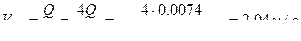 где
где 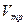 - скорость в трубе
- скорость в трубе
Согласно уравнению Бернулли 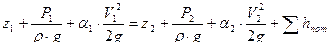
 . Принимаем V1=0 и V2=0
. Принимаем V1=0 и V2=0
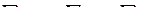 ,
, 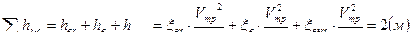
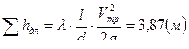 ,
, 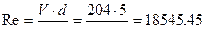 ,
, 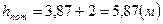
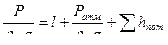 =>
=> 
Дата: 2018-12-28, просмотров: 1312.