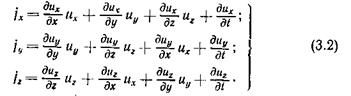Виды движения жидкости. Основные понятия кинематики жидкости: линия тока, элементарная струйка и ее свойства, живое сечение, расход объемный и массовый. Поток жидкости. Средняя скорость. Уравнение постоянство расхода. Дифференциальные уравнения движения Эйлера. Уравнение Бернулли для элементарной струйки идеальной жидкости. Геометрическое и энергетическое толкование уравнения Бернулли. Гидравлическое сопротивление.

Тема 3.2. Вихревое движение жидкости.

Вихревая линия, вихревая трубка, их свойства. Угловая ско­рость вращения частицы жидкости. Теорема Гельмгольца о вихревом движении. Уравнение безвихревого (потенциального) движения жид­кости.

Указания к темам 3.1. и 3.2.

Способы описания движения.

Движущаяся жидкость представляет сплошную среду сово­купности частиц, которые перемещаются с различными параме­трами, изменяющимися в зависимости от координат и времени.

Частица сплошной среды — это весьма малый элемент объема среды (элементарный объем), который можно считать точечным.

В кинематике жидкости возможны два способа описания движения — Лагранжа и Эйлера.

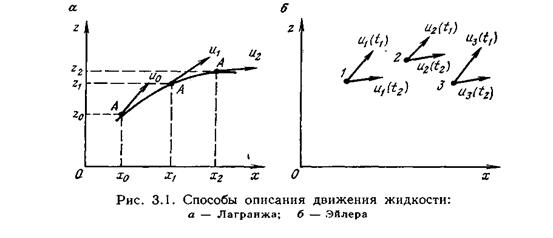
По способу Лагранжа движение жидкости задается путем указания зависимости координат определенной (намеченной) частицы жидкости от времени. Движущаяся частица жидкости описывает в пространстве траекторию, вдоль которой изменяется скорость.

На рис. 3.1, а показана траектория движения частицы А в неподвижной системе координат, где за определенное время координаты частицы изменялись с х₀, z₀ на x_lt z₁ за время t₁ ; х₂, z₂ за время t_z и т. д. Таким образом, при описании движения пере­менными являются скорость, ускорение и координаты частицы. Практически для большинства инженерных задач нет необходи­мости в знании параметров движения отдельных частиц, поэтому способ Лагранжа применяется только в особых случаях: например, Для описания переноса жидкостью мельчайших твердых частиц (ила).

Способ Эйлера заключается в том, что движение определяется полем скоростей жидкости в пространстве в каждый момент времени, т. е. описывается движение различных частиц, проходящих через намеченные точки пространства, заполненного жидкостью. При этом переменными являются скорости частиц, а координаты точки пространства, через которые проходят частицы, остаются постоянными (известными).

На рис. 3.1, б показаны зафиксированные точки 1, 2, 3 в пространстве, через которые в разное время t₁  , t₂ проходят частицы co скоростями u₁(t₁), u₂(t₁), u₃(t₁),

u₁(t₂),u₂(t₂),u₃(t₂).

Последнее обстоятельство значительно облегчает проведение теоретических и экспериментальных исследований, так как координаты зафиксированных точек в пространстве известны и постоянны.

При решении большинства инженерных задач необходимо знать, с какими скоростями различные частицы жидкости про­ходят через определенные элементы конструкций или инженерных сооружений или подходят к ним. Поэтому способ описания движения Эйлера принят основным.

По Эйлеру задано поле скоростей жидкости в пространстве в каждый момент времени в проекциях скорости и на оси непо­движной прямоугольной декартовой системы координат:

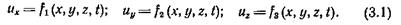
Проекции ускорений элементарных объемов среды в этой системе координат по правилу дифференцирования сложной функции будут:

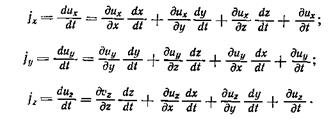
Зная, что 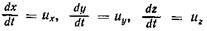   являются проекциями скорости и в момент времени t, и подставляя их в уравне­ния проекций ускорений, получим:

Рассмотрим кинематический смысл каждого слагаемого в правой части системы уравнений (3,2).

Последние слагаемые du/dt представляют проекции локального ускорения, которое обусловливается изменением поля скоростей со временем при фиксированных координатах, т. е. местным локальным изменением.

Первые три слагаемые в правой части (3.2) дают проекции конвективного ускорения, которое образуется за счет изменения координат частицы, соответствующих ее передвижению (конвекции).

Конвективное ускорение возможно только при движении жидкости и газов.

ВИДЫ ДВИЖЕНИЯ