Истечение жидкости через отверстие в тонкой стенке при постоянном напоре. Определение скорости истечения и расхода жидкости. Коэффициенты сжатия, скорости и расхода. Истечение жидкости в атмосферу и под уровень. Расчет времени опорожнения и заполнения судовых отсеков и цистерн. Истечение через насадки. Виды и сравнительная характеристика применяемых в судовой технике насадков. Истечение жидкости при переменном напоре.
Указания к теме 4.6.
1. При установившемся истечении жидкости из большого открытого резервуара через круглое отверстие, размер которого мал по сравнению с его заглублением под уровнем жидкости (малое отверстие, рис. VI—1), средняя скорость в сжатом сечении струи равна по уравнению Бернулли:
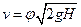, (1)
где Н — глубина центра тяжести сжатого сечения струи под уровнем (напор истечения).
Безразмерный коэффициент скорости:
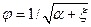, (2)
где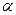 
— коэффициент кинетической энергии в сжатом сечении струи; 
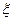— коэффициент сопротивления отверстия, выражающий потерю напора при истечении в долях скоростного напора струи, подсчитанного по средней скорости.
В общем случае истечения из замкнутого резервуара в газообразную среду (рис. VI—2) напор истечения Н представляет разность значений гидростатического напора в резервуаре и в центре сжатого сечения струи;
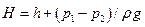, (3)
где Н — глубина центра сжатого сечения струи под уровнем жидкости; р1 — давление в резервуаре над жидкостью; р2 — давление среды, в которую вытекает струя;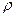 
— плотность жидкости.
Если истечение происходит в атмосферу, напор истечения представляет глубину расположения центра сжатого сечения струи под пьезометрическим уровнем (уровнем атмосферного давления) в резервуаре:
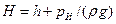, (4)
где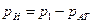 
— избыточное давление в резервуаре над жидкостью.
Степень сжатия струи, вытекающей через отверстие, характеризуется коэффициентом сжатия:
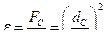, (5)
где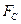 
, 
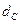— площадь и диаметр сжатого сечения струи; 
, 
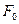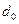— площадь и диаметр отверстия.
Расход через отверстие:
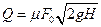, (6)
где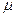 
— коэффициент расхода,
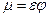. (7)
Значения коэффициентов истечения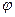 
, 
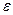и 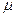круглого малого отверстия зависят от формы его кромок, условии подтока жидкости к отверстию и числа Рейнольдса, определяемого как
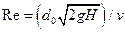, (8)
где v — кинематическая вязкость жидкости. ( Коэффициенты истечения отверстий малых абсолютных размеров зависят также от числа Вебера, выражающего влияние поверхностного натяжения жидкости: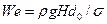 
, где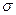 
— поверхностное натяжение на границе струи с газообразное средой, Н/м. При 
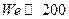влияние поверхностного натяжения практически отсутствует зона автомодельности по We )
Зависимость коэффициентов истечения от R е для малого круглого отверстия с острой кромкой дана в обработке А. Д. Альтшуля на рис. VI—3.
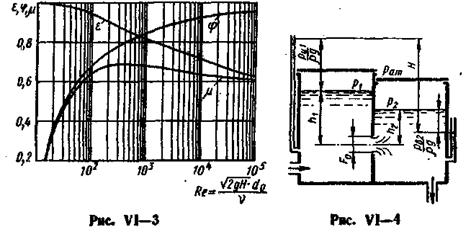
Значения 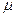в функции R е приведены ниже:
| Re |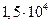 
| 
| 
| 
| 
| 
| 
|
|
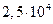
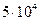
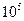
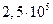
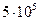
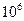
| 0,638 | 0,623 | 0,610 | 0,603 | 0,597 | 0,594 | 0,593 |
При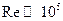 
число Рейнольдса практически не влияет на коэффициенты истечения (квадратичная зона истечения), и для расчетов можно пользоваться следующими , их средними значениями:
; 
; 
.
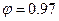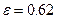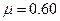При этом неравномерность скоростей в сжатом сечении струи весьма невелика и можно принимать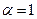 
.Тогда
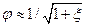, (9)
откуда в среднем для круглого отверстия с острой кромкой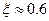 
.
Коэффициент полезного действия отверстия — отношение удельной кинетической энергии струи к напору истечения:
.
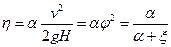При больших R е можно пользоваться выражением:
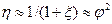. (10)
Для малых отверстий других форм при больших R е значения коэффициента расхода в формуле (6) можно принимать равными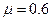 
.
2. При истечении под уровень (рис. VI— 4) скорость жидкости в сжатом сечении струи и расход определяются по формулам (1) и (6), в которых напор истечения Н представляет разность гидростатических напоров (выражаемую разностью пьезометрических уровней) в резервуарах:
. (11)
Значения коэффициентов истечения для затопленного отверстия можно принимать такими же, как при истечении свободной струи в атмосферу. При истечении через затопленное отверстие расход не зависит от глубины расположения отверстия под уровнями.
3. Приведенные выше значения коэффициентов истечения относятся к так называемому совершенному сжатию струи, когда боковые стенки резервуара значительно удалены от отверстия (на расстоянии более трех линейных размеров отверстия) и не влияют на формирование струи. При расположении боковых стенок вблизи отверстия их направляющее действие уменьшает степень сжатия струн; при этом коэффициенты сжатия струи и расхода возрастают.
При истечении из цилиндрического резервуара площадью F 1 через круглое отверстие площадью F 0 , расположенное на его оси (рис. VI—5), среднее значение коэффициента сжатия струи при больших значениях R е можно определять по эмпирической формуле:
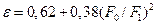(12)
4. Скорость истечения и расход жидкости при истечении из резервуара ограниченной площади (рис. VI—5) определяются с помощью уравнений Бернулли и расхода,
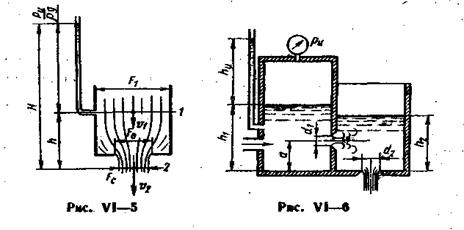
записанных для сечения в резервуаре перед отверстием (сечение 1) и сжатого сечения струи (сечение 2):
;
.
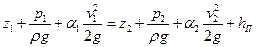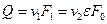Выражая потерю напора как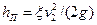 
и вводя напор истечения Н, представляющий разность гидростатических напоров в сечениях 1 и 2:
,
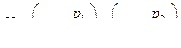получим скорость истечения
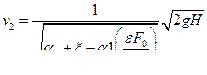(13)
и расход:
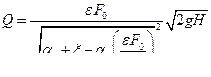(14)
В квадратичной зоне истечения можно приближенно принимать значения коэффициента кинетической энергии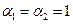 
и коэффициента сопротивления отверстия 
.
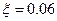Для предельного случая неограниченного резервуара (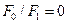 
) формулы (13) и (14) переходят в приведенные выше формулы (1) и (6).
5. Расход через большое отверстие, вертикальный размер которого одного порядка с напором истечения, определяется по общей формуле (6), в которой Н — напор истечения, отнесенный к высоте расположения
центра тяжести отверстия (при истечении в атмосферу из открытого резервуара — к глубине центра тяжести отверстия под свободной поверхностью).
На коэффициент расхода 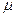большого отверстия, помимо факторов, указанных для малого отверстия, влияет также число Фруда:
,
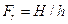где h — вертикальный размер отверстия.
Для больших отверстий с острой кромкой коэффициент расхода в квадратичной области истечения изменяется при разных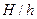 
в пределах 
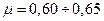. При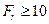 
процесс истечения становится практически автомодельным относительно числа Фруда.
6. В качестве примера расчета процесса истечения рассмотрим схему на рис. VI—6, в которой жидкость плотностью 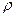, нагнетаемая в бак, перетекает из его левой замкнутой секции в открытую правую секцию через отверстие диаметром 
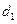(расположенное в боковой стенке на высоте а) и вытекает затем в атмосферу через донное отверстие диаметром 
.
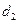Определим для установившегося режима системы расход Q из бака и высоту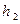 
уровня в правой секции, считая известными высоту уровня 
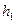и показание манометра 
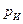в левой секции.
Исходным для решения задачи является условие равенства расходов через боковое и донное отверстия при установившемся режиме (т. е. при постоянных уровнях, жидкости). Для выбора расчетных зависимостей необходимо предварительно выяснить условия истечения жидкости через боковое отверстие. Для этого предположим, что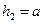 
, тогда расход через боковое отверстие:
,
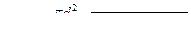где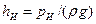 
— высота пьезометрического уровня в левой секции.
Расход через донное отверстие:
.
|
|
|
|
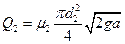Если окажется, что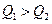 
, то в действительности 
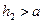и боковое отверстие затоплено; если 
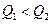, то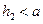 
и боковое отверстие не затоплено.
В первом случае условие равенства расходов дает систему уравнений
,
из которой определяются уровень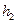 
и расход Q .
Во втором случае:
.
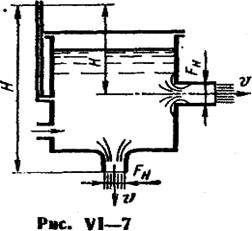
7. При истечении жидкости из больших резервуаров через насадки (короткие трубки различной формы, рис. VI—7) скорость истечения на выходе из насадка и расход определяются по формулам (7) и (6). В формуле (6) Fo заменяется выходной площадью насадка Fu . Для плавно сужающегося насадка без сжатия струи на выходе (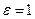 
) можно принимать в квадратичной зоне сопротивления 
.
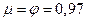Для некоторых насадок коэффициенты истечения могут быть приближенно определены расчетом, путем суммирования потерь на отдельных участках потока.
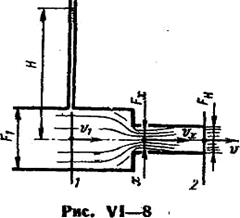
Так, например, для внешнего цилиндрического насадка (рис. VI—8) потерю напора можно представить в виде суммы:
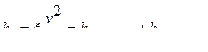
где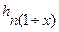 
— потеря при входе в насадок на участке до сжатого сечения струи (х); 
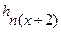— потеря при расширении потока на участке между сжатым и выходным сечениями.
Предполагая, наличие квадратичной зоны истечения и выражая эти потери по формулам:
; 
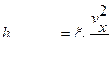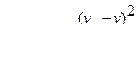
получим
,
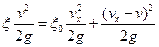где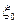 
— коэффициент сопротивления отверстия с острой кромкой; 
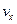— скорость в сжатом сечении струи.
По уравнению расхода:
; 
,
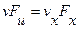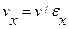где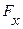 
— площадь сжатого сечения; 
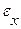— коэффициент сжатия струи при входе в насадок.
Значение 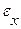зависит от соотношения площадей насадка 
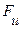и резервуара F 1 и может быть определено по формуле (12).
Подставляя в выражение суммы потерь значение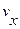 
, находим коэффициент сопротивления насадка:
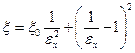, (15)
при помощи, которого определяются скорость истечения и расход (сжатие струи на выходе из насадка отсутствует):
;
.
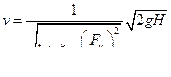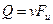При истечении из большого резервуара (рис. VI—9) сжатие струи в сечении х является совершенным, и расчет дает в этом случае (для средних значени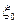й и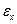 
) 
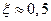. Скорость и расход определяются по форму (1) и (6), в которых:
.
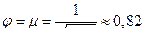По опытным данным, коэффициент расхода цилиндрического насадка в квадратичной зоне сопротивления, при длинах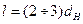 
составляет 
.
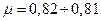Наглядно представление об изменениях напора потока и его составляющих при истечении жидкости через насадок дается графиком напоров (см. рис. VI—9). Линия напора и пьезометрическая линия на этом графике качественно изображают ход изменения полного и гидростатического напоров по длине насадка от начального сечения перед входом в насадок до его выходного сечения. Пьезометрический напор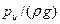 
в любом сечении насадка определяется расстоянием по вертикали от оси насадка до пьезометрической линии, скоростной напор 
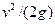— расстоянием по вертикали между пьезометрической линией и линией напора.
8. Если в промежуточных сечениях насадка скорости имеют большие значения, чем скорость выхода из насадка, то в этих сечениях при истечении в атмосферу возникает вакуум (пьезометрическая линия проходит здесь ниже оси насадка).
Так, например, наибольший вакуум рв, возникающий внутри цилиндрического насадка в сжатом сечении струи, определяется из выражения:
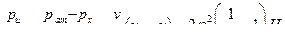(16)
Истечение через насадок в атмосферу с заполнением выходного сечения насадка возможно только при напорах, меньших предельного H пр, который соответствует падению абсолютного давления в сжатом сечении до давления насыщенных паров жидкости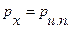 
: 
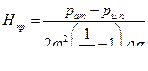(17)
При H > H пр происходит срыв режима работы насадка: струя отрывается от стенок, и процесс сменяется истечением через отверстие с острой кромкой.
При истечении через затопленный насадок его работа под более высоким напором, чем некоторое предельное значение (зависящее от заглубления насадка), сопровождается кавитацией.
9. Приведем в виде примера расчет истечения в атмосферу из большого резервуара через конический насадок с плавно скругленным входом под постоянным статическим напором Н (рис. VI—10).
Заданы входной d и выходной D диаметры диффузора, а также коэффициент сопротивления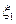 
входного участка насадка и коэффициент потерь 
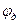в диффузоре.
1. Определить расход Q через насадок и построить график напоров по его длине.
2. Найти предельный напор Нпр насадка.
3. Определить, при каком выходном диаметре D пропускная способность насадка будет максимальной.
Для рассматриваемого насадка (предполагая квадратичную зону истечения и пренебрегая неравномерностью распределения скоростей по сечению) имеем:
,
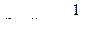где 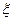— коэффициент сопротивления насадка.
Пользуясь приемом суммирования потерь, получаем:
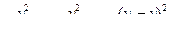
где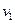 
и 
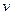— скорости во входном и выходном сечениях диффузора.
Так как по уравнению расхода:
,
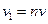то коэффициент сопротивления
,
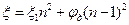где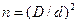 
Скорость истечения и расход:
; 
.
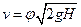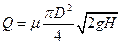Построение графика напоров дано на рис. VI—10. Наибольший вакуум имеет место во входном сечении диффузора. По уравнению Бернулли для движения жидкости в диффузоре:
.
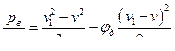Последнее соотношение позволяет рассчитать предельный напор насадка; используя подстановку 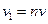, приведем выражение для вакуума к виду:
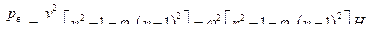
Подставляя далее выражение 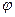через 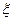, а также максимальное значение вакуума 
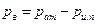, получим для предельного напора
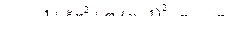
Для определения выходного диаметра D , отвечающего максимальной пропускной способности насадка (максимальному расходу при данном напоре), удобнее всего воспользоваться уравнением Бернулли, записанным для свободной поверхности жидкости в резервуаре и для выходного сечения насадка:
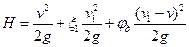
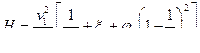
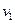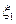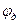Максимальному значению скорости (и, следовательно, расхода) при постоянном Н отвечает минимум выражения в квадратных скобках. Исследуя, это выражение на минимум, получаем (принимая и постоянными):
; 
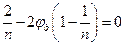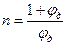
Следовательно, искомый выходной диаметр :
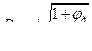
Заметим, что насадок такого диаметра характеризуется максимальным вакуумом во входном сечении диффузора при данном напоре истечения и, следовательно, минимальным предельным напором.
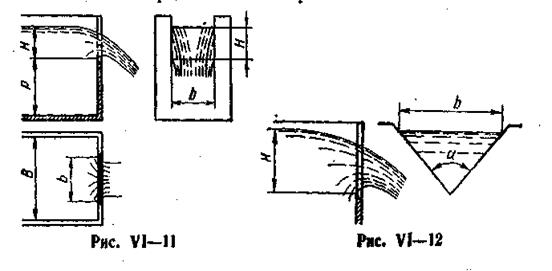
10. Расход через незатопленный прямоугольный водослив в тонкой стенке (рис. VI—11)
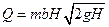, (18)
где т — коэффициент расхода; b — ширина порога водослива; Н — напор над порогом водослива.
При истечении свободной струей коэффициент расхода водослива можно определить по эмпирической формуле (все размеры в метрах):
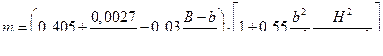. (19)
У водослива без бокового сжатия b= В. Для треугольного водослива с углом а при вершине (рис. VI—12)
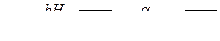, (20)
где коэффициент расхода можно в среднем принимать т = 0,32.
Вопросы для самопроверки.
1. Чем вызвано сжатие струи при истечении жидкости через отверстие с острой кромкой?
2. Как связаны между собой коэффициенты сжатия, скорости, расхода?
3. В чем заключается физический смысл этих коэффициентов?
4. Почему эти коэффициенты для отверстия меньше единицы?
5. Что называется насадком?
5. Какие типы насадков существуют? Охарактеризуйте эффект от применения различных типов насадков и области их использования.
7. Какое влияние на расход жидкости оказывает ее вязкость при истечении из отверстия и насадка?
Литература: 1, 2, 3
Задачи.
1. Определить до какого набольшего избыточного давления Ри сжатого воздуха над поверхностью бензина в баке истечение через цилиндрические насадок будет происходить с заполнением его выходного сечения.
Уровень бензина в баке h = 1,5 м. Атмосферное давление p атм. Принять коэффициент расхода насадки μ=0,81 и коэффициент сжатия струи при входе ε.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| h, м | 1,5 | 2 | 2,5 | 1 | 1,5 | 2 | 2,5 | 1,5 | 1 | 2 |
| pатм, кПа | 97 | 98 | 99 | 96 | 95 | 97 | 93 | 94 | 95 | 96 |
| μ | 0,81 | 0,82 | 0,83 | 0,84 | 0,85 | 0,86 | 0,87 | 0,82 | 0,83 | 0,84 |
| ε | 0,62 | 0,64 | 0,66 | 0,68 | 0,7 | 0,62 | 0,64 | 0,66 | 0,68 | 0,62 |
2. Определить скорость перемещение поршня вниз, если к его штоку приложена сила F. Поршень диаметром D имеет пять отверстии диаметром d0 каждое. Отверстие рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ, ρ.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| F, кН | 10 | 12,5 | 15 | 17,5 | 10 | 10,5 | 10 | 10 | 12,5 | 15 |
| μ | 0,81 | 0,82 | 0,83 | 0,84 | 0,85 | 0,86 | 0,87 | 0,82 | 0,83 | 0,84 |
| D,мм | 8 | 9 | 10 | 7 | 6 | 8 | 9 | 10 | 6 | 7 |
| d0, мм | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | 2 | 3 |
| ρ,кг/м3 | 900 | 900 | 900 | 900 | 900 | 900 | 900 | 900 | 900 | 900 |
3.Для увеличения пропускной способности плавно сходящегося насадка, выходной диаметр которого d = 80 мм и коэффициент сопротивления ξ =0,04, к нему присоединен цилиндрический патрубок. Определить D патрубка, при котором пропускная способность получена, т.о. составного насадка будет наибольшей.
| Исходные данные | Последняя цифра шифра | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| d, мм | 80 | 90 | 100 | 70 | 60 | 50 | 80 | 90 | 60 | 50 |
| ζ | 0,04 | 0,06 | 0,04 | 0,08 | 0,06 | 0,04 | 0,08 | 0,06 | 0,04 | 0,08 |
Примеры решения задач
Задача 1.
Определить, пренебрегая потерями напора, начальную скорость истечения жидкости из сосуда, заполненного слоем воды и масла (относительная плотность δ = 0,8) одинаковой высоты h = 1 м. Определить начальную скорость истечения при заполнении сосуда только водой или только маслом до уровня 2h.
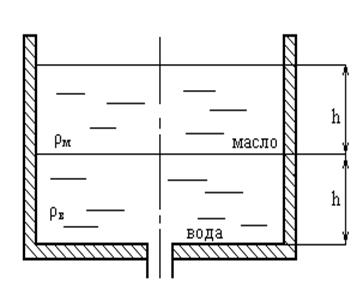
Решение.
Скорость истечения
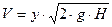, где y – коэффициент скорости, для малого отверстия y = 1
Эквивалентный напор двух жидкостей определяется из условия
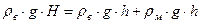следовательно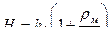 
Тогда скорость будет равна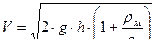 
; 
Если оба слоя жидкости – вода, то при ρм = ρв получим
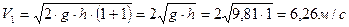
Задача 2.
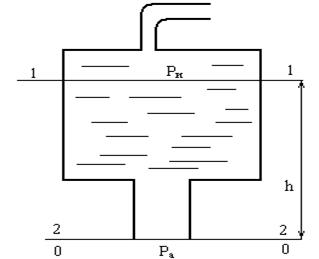
Определить до какого набольшего избыточного давления Ри сжатого воздуха над поверхностью бензина в баке истечение через цилиндрические насадок будет происходить с заполнением его выходного сечения.
Уровень бензина в баке h = 1,5 м. Плотность бензина ρ = 750 кг/м3. Атмосферное давление 97 кПа. Принять коэффициент расхода насадки μ=0,81 и коэффициент сжатия струи при входе ε = 0,62.
Решение.
Запишем уравнение Бернулли.
; 
; 
; 
; 
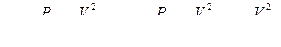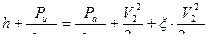
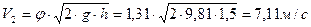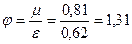
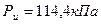
Задача 3.
Определить расход воды Q через отверстие с острой кромкой диаметром d=120 мм, выполненное в торце трубы диаметром D = 200 мм, если показание манометра перед отверстием Рм = 0,1 МПа и высота расположения манометра над осью трубы h = 1,3 м. Коэффициент сопротивления отверстия принять ξ = 0,04
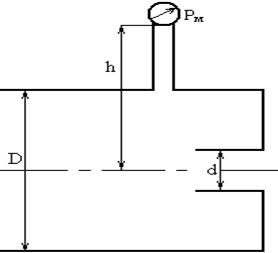
Решение.
1. По формуле расхода определим:
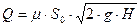(1)
; 
; 
,
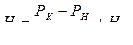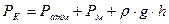где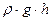 
- давление
столба жидкости;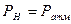 
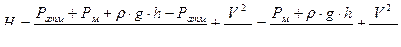
Скорость: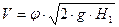 
; 
; 
;
;
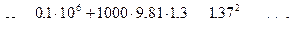
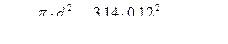μ – коэффициент расхода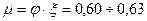 
(для круглых отверстий) Принимаем μ = 0,628
Подставляем все в уравнения (1), получим:
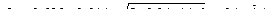
Задача 4.
Через водоспускную платину, имеющую форму цилиндрической насадки, необходимо пропускать расход Q = 2,3 м3/с при напоре H = 10 м. Определить диаметр водоспуска d и минимальную глубину h затопления его оси под уровень необходимую, чтобы вакуумметрическая высота внутри насадка не превосходила 6 м. Принять коэффициент расхода насадка μ = 0,82 и коэффициент сжатия струи при входе в насадок ξ = 0,63
Решение.
1. Определяем минимальную глубину h
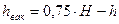, тогда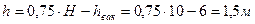 
2. Определяем диаметр водоспуска из формулы
; 
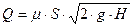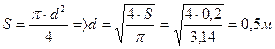
Задача 5.
Определить скорость перемещение поршня вниз, если к его штоку приложена сила F=10 кН. Поршень диаметром D=50 мм имеет пять отверстии диаметром d0=2 мм каждое. Отверстие рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ=0,82, ρ=900кг/м3
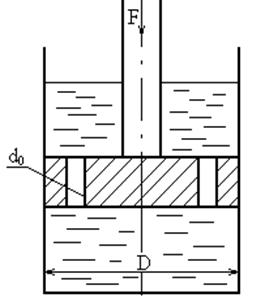
Решение.
1. Определим расход
, 
, 
, 
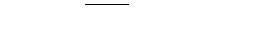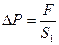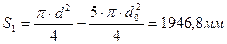
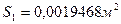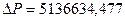
2. Определяем скорость перемещения поршня
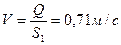
Задача 6.
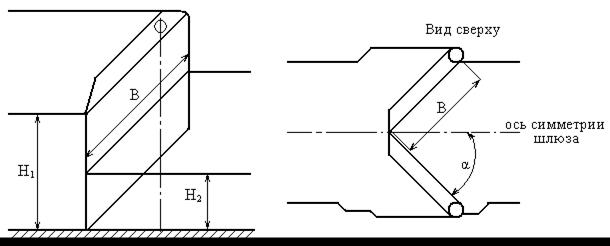
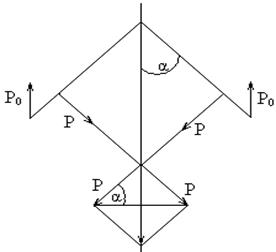
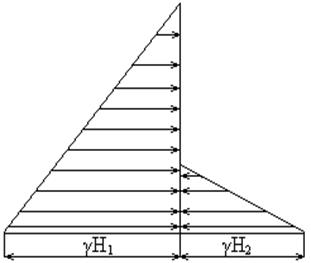
Двухстворчатые ворота отгораживают шлюзовую камеру от канала с низовой стороны шлюза. Они имеют две симметричные поворотные створки, соприкасающиеся в закрытом положении по плоскости, которая совпадает с продольной осью симметрии шлюза. При заполненном шлюзе вода по обе стороны ворот находиться на уровнях Н1 = 18 м, Н2 = 6 м.
Найти равнодействующую Р сил давления воды на каждую из створок ворот. На какой высоте х от дна приходит линия действия силы Р?
Построить эпюры нагрузки от воздействия воды на поверхность ворот.
При решении поверхность створки считать плоской шириной В = 16 м, α=700.
Определить силу Р0, воспринимаемую опорами, расположенными на оси вращения О каждой из створок.
Решение.
Сила давления, связанная с действием воды
; 
; 
; 
; 
; 
; 
; 
; 
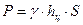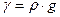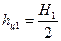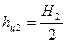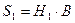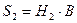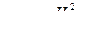Точки приложения сил Р1 и Р2
; 
; 
; 
; 
; 
; 
; 
; 
; 
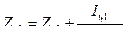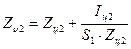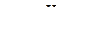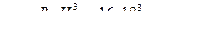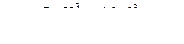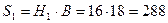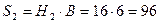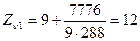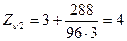
Правило моментов
; 
; 
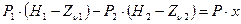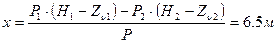
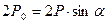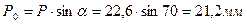
Эпюра
Задача 7.
Для увеличения пропускной способности плавно сходящегося насадка, выходной диаметр которого d = 80 мм и коэффициент сопротивления ξ =0,04, к нему присоединен цилиндрический патрубок. 1) Определить D патрубка, при котором пропускная способность получена, т.о. составного насадка будет наибольшей. 2) Для этого же насадка определить в случае истечения воды в атмосферу предельный напор, при котором вакуум в узлах сечения насадка достигнет 0,1 МПа.
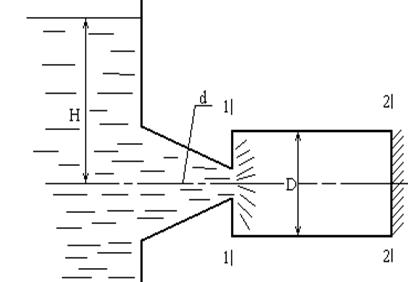
Решение.
1) 
; 
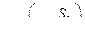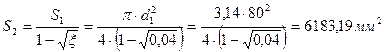
2) 
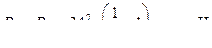; принимаем φ = 0,8; ξ = 0,63
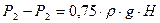; Р2=Ратм=102 кПа; Рвак=Ратм-Рабс;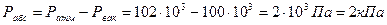 
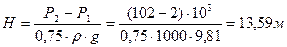
Задача 8.
Считая жидкость не сжимаемой, определить скорость движения поршня под действием силы F=10кН на штоке, диаметр поршня D = 80 мм, диаметр штока d = 30 мм, проходное сечение дросселя Sдр = 2 мм2, его коэффициент расхода μ = 0,75, избыточное давление слива Рс = 0, плотность рабочей жидкости ρ = 900 кг/м3
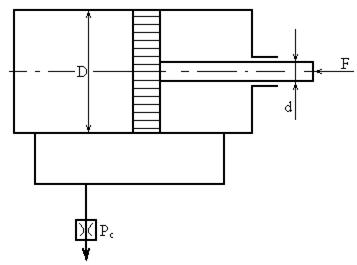
Решение.
1. Определить давление в гидросистеме:
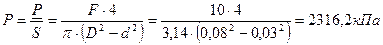
2. Определяем расход Q:
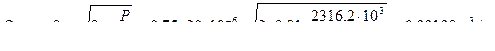
3. Определяем скорость движения поршня V:
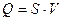следовательно, получим
Дата: 2018-12-28, просмотров: 1185.
