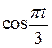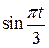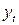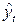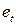Последовательность значений случайного показателя 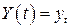 в последовательные моменты времени:
в последовательные моменты времени: 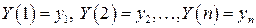 - называют временным рядом.
- называют временным рядом.
К числу наиболее простых моделей нестационарных временных рядов относятся регрессионная модель аддитивного типа

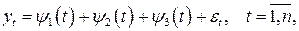
и регрессионная модель мультипликативного типа:
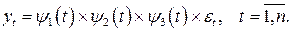
В случае регрессионной модели аддитивного типа ее компоненты имеют следующую интерпретацию:
-
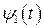 - тренд временного ряда (некоторая неслучайная функция, отражающая долговременную тенденцию в изменении показателя
- тренд временного ряда (некоторая неслучайная функция, отражающая долговременную тенденцию в изменении показателя 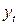 ; чаще всего эта тенденция описывается с помощью монотонной функции полиномиального типа;
; чаще всего эта тенденция описывается с помощью монотонной функции полиномиального типа; -
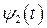 - сезонная компонента временного ряда (некоторая неслучайная функция, отражающая периодически повторяющиеся через определенные промежутки времени колебания анализируемого показателя); эта компонента описывается с помощью периодических функций, в аналитическом представлении которых присутствуют гармоники (тригонометрические функции); период
- сезонная компонента временного ряда (некоторая неслучайная функция, отражающая периодически повторяющиеся через определенные промежутки времени колебания анализируемого показателя); эта компонента описывается с помощью периодических функций, в аналитическом представлении которых присутствуют гармоники (тригонометрические функции); период 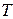 гармоники определяется содержательной сущностью задачи; в описании модели могут присутствовать несколько сезонных компонент. Чаще всего описание таких компонент осуществляется с помощью частичных сумм ряда Фурье следующего вида:
гармоники определяется содержательной сущностью задачи; в описании модели могут присутствовать несколько сезонных компонент. Чаще всего описание таких компонент осуществляется с помощью частичных сумм ряда Фурье следующего вида:
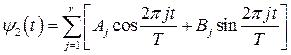 ; (3.12)
; (3.12)
-
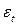 - случайная ошибка модели.
- случайная ошибка модели.
Например, регрессионная модель вида
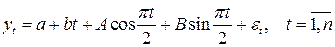
позволяет описать временной ряд, содержащий линейную трендовую составляющую и сезонную составляющую с периодом 4.
В условиях классических предположений анализ модели временного ряда регрессионного типа осуществляется теми же средствами, что и множественная линейная регрессионная модель.
Другой возможный способ построения подобных моделей предполагает использование для описания сезонных составляющих фиктивных переменных, и он был рассмотрен в предыдущем разделе.
Пример 3.4. Имеются данные (в млн. руб.) об объемах продаж торгового дома за 12 месяцев
Месяц
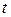
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Объем
Продаж
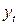
| 200 | 310 | 320 | 260 | 190 | 210 | 310 | 410 | 430 | 370 | 300 | 320 |
Построить подходящую модель временного ряда.
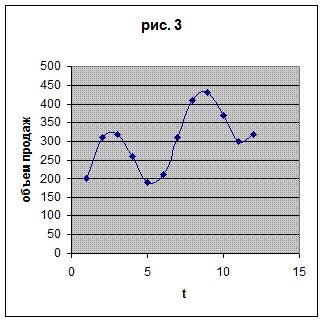
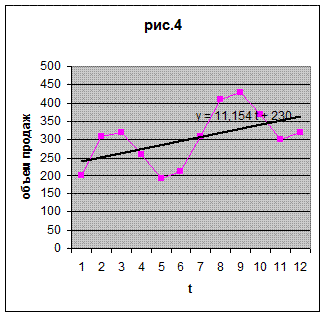
Решение. Подвергнем анализу график временного ряда, представленный на рис.3. Хорошо заметна линейная тенденция в изменении объема продаж. На рис.4 к графику временного ряда добавлена линия линейного тренда 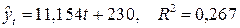 . При этом хорошо стали заметны колебания временного ряда относительно тренда сезонного характера с периодом 6.
. При этом хорошо стали заметны колебания временного ряда относительно тренда сезонного характера с периодом 6.
| 
|
Поэтому будем строить модель временного ряда, содержащую линейную трендовую компоненту, а также сезонную компоненту с периодом 6 и одной гармоникой. Выбор одной гармоники обусловлен малым количеством исходных данных (имеются всего результаты 12 наблюдений). Таким образом, предлагается следующий вариант описания данных:
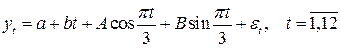 . (3.12)
. (3.12)
Получилась линейная по параметрам регрессионная модель. Неизвестные оценки параметров 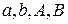 модели найдем, воспользовавшись обычным методом наименьших квадратов. Результаты промежуточных вычислений приведены в следующей таблице
модели найдем, воспользовавшись обычным методом наименьших квадратов. Результаты промежуточных вычислений приведены в следующей таблице
|
|
|
|
|
| Остатки |
| 1 | 0,50 | 0,87 | 200,00 | 201,84 | -1,84 |
| 2 | -0,50 | 0,87 | 310,00 | 303,89 | 6,11 |
| 3 | -1,00 | 0,00 | 320,00 | 323,06 | -3,06 |
| 4 | -0,50 | -0,87 | 260,00 | 258,28 | 1,72 |
| 5 | 0,50 | -0,87 | 190,00 | 192,45 | -2,45 |
| 6 | 1,00 | 0,00 | 210,00 | 209,50 | 0,50 |
| 7 | 0,50 | 0,87 | 310,00 | 310,50 | -0,50 |
| 8 | -0,50 | 0,87 | 410,00 | 412,55 | -2,55 |
| 9 | -1,00 | 0,00 | 430,00 | 431,72 | -1,72 |
| 10 | -0,50 | -0,87 | 370,00 | 366,94 | 3,06 |
| 11 | 0,50 | -0,87 | 300,00 | 301,11 | -1,11 |
| 12 | 1,00 | 0,00 | 320,00 | 318,16 | 1,84 |
После применения метода наименьших квадратов получим следующую оценку функцию регрессии
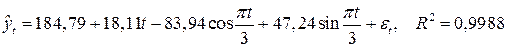
Дата: 2018-12-28, просмотров: 335.