Множественный коэффициент корреляции, соответствующий модели наблюдений (2.2), также как и в случае парной модели, определяется с помощью соотношения:

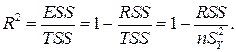                              (2.14)

Применительно к множественной линейной регрессионной модели коэффициент детерминации определяет долю дисперсии зависимой переменной, объясненную множественной функцией регрессии 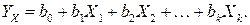Разложение (2.14) справедливо только при наличии постоянной составляющей в модели (2.1).

Величину

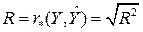                             (2.16)

принято называть множественным коэффициентом корреляции (multiple-R). Чем ближе его значение к единице, тем в большей степени можно считать, что имеющиеся данные связаны множественной линейной регрессионной зависимостью.

  Известно, что включение в модель (2.1) - (2.2) одной или нескольких новых переменных может привести только к увеличению 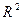. Коэффициент детерминации не может уменьшиться даже при включении в модель несущественных переменных. Более того, включением в модель достаточно большого числа переменных можно добиться того, что значение коэффициента детерминации станет равным единице. По этой причине для сравнения моделей с различных числом факторов вместо  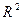обычно используется скорректированный коэффициент детерминации с поправкой на число степеней свободы:

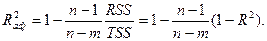           (2.17)

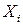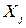Если увеличение доли объясненной регрессии при добавлении новой переменной мало, то скорректированный коэффициент детерминации может уменьшиться, следовательно, добавлять переменную нецелесообразно. Кроме того, если объясняющие переменные  и  сильно коррелируют между собой, то они объясняют одну и ту же часть разброса значений переменной 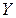, и в этом случае трудно оценить вклад каждой из переменных в объяснение поведения 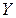. 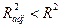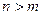Очевидно, что  при  и 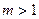. При использовании коэффициента  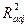для выбора между конкурирующими моделями лучшей признается та из них, для которой этот коэффициент принимает максимальное значение.

Частный коэффициент корреляции используется для измерения силы «очищенной» линейной связи между двумя заданными переменными. Такое применение частного коэффициента корреляции теоретически обосновано лишь в том случае, когда переменные 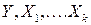 имеют совместное нормальное распределение. Во всех остальных случаях подобное использование носит эвристический характер.

  Для трех переменных 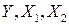 формула (2.20) может быть записана в более простой форме:

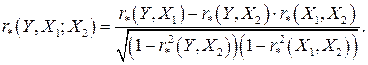(2.21)

Продолжение примера 2.1. Определить коэффициенты детерминации и скорректированный коэффициент детерминации. Сделать выводы.

Решение. Для нахождения коэффициента детерминации воспользуемся формулой (2.12):

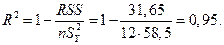
Вывод: Доля дисперсии зависимой переменной 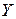, объясненная построенной линейной моделью составляет 95%, остальные 5% дисперсии объяснить не удалось.

Скорректированный коэффициент детерминации вычисляем по формуле (2.17):

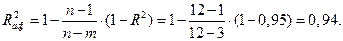
Для интерпретации скорректированного коэффициента детерминации оценим модель без включения в нее независимой переменной 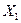, т.е рассмотрим зависимость

объема продаж услуг 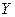 (в млн. руб.) некоторого сервисного предприятия от объема основных производственных средств  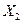(в млн. руб.).

Поэтому выборочное уравнение регрессии, характеризующее зависимость объема продаж услуг от объема основных производственных средств имеет вид:

.

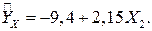Коэффициент детерминации равен: 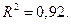 Скорректированный коэффициент детерминации равен: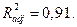

Вывод. Поскольку скорректированный коэффициент детерминации для парной модели меньше, чем для множественной, то лучшей признается множественная линейная регрессионная модель с включенными в нее переменным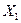и  и .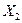

С целью анализа совокупной значимости коэффициентов уравнения линейной регрессии проверяют гипотезу о статистической значимости коэффициента детерминации. Гипотеза 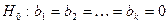 (равенство нулю всех коэффициентов регрессии при независимых переменных) эквивалентна гипотезе:  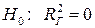(генеральный коэффициент корреляции равен нулю, модель не значима) против конкурирующей:  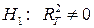(модель в целом значима).

  Для проверки этой гипотезы используется 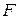- статистика следующего вида

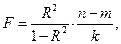                                                                          (2.22)        

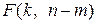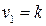которая в условиях справедливости нулевой гипотезы имеет распределение Фишера  с  и 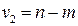 степенями свободы. По этой формуле находится  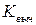- вычисленное значение 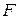- статистики. Критическое значение 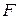-статистики определяется по табл. 5 и 6: 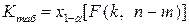. Если 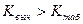, то гипотезу о значимости модели  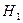следует принять, а гипотезу  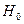отклонить.

Продолжение примера 2.1. На уровне значимости 0,05 проверить гипотезу о значимости модели.

Решение. Проверим гипотезу о значимости модели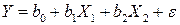

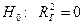 (модель не значима).

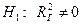 (модель значима).

По формуле (2.20) вычислим значение 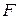-статистики:

.

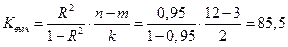Критическое значение статистики находим по табл. 6:

.

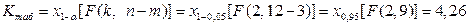Так как 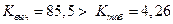, то гипотезу о не значимости модели  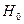следует отвергнуть. На уровне значимости 0,05 можно утверждать, что модель значима.