Проверка статистических гипотез о коэффициентах множественной линейной регрессии осуществляется также, как и в случае парной, с помощью 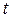 -статистик, которые в условиях справедливости нулевой гипотезы имеют распределения Стьюдента с
-статистик, которые в условиях справедливости нулевой гипотезы имеют распределения Стьюдента с 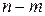 степенями свободы.
степенями свободы.
Проверка гипотезы о статистической значимости параметров регрессии.
На формальном языке проверяется нулевая гипотеза 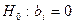 (коэффициент регрессии не значим) против конкурирующей
(коэффициент регрессии не значим) против конкурирующей 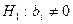 (коэффициент регрессии значим).
(коэффициент регрессии значим).
Проверка этой гипотезы производится аналогично проверке для модели парной линейной регрессии. Для решения этой задачи используется 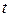 -статистика вида:
-статистика вида:
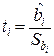 . (2.8)
. (2.8)
По этой формуле находится расчетное значение статистики 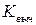 . Все остальные действия проводятся по той же схеме, что и при проверке гипотезы о значении коэффициента. То же самое можно сказать и о проверке гипотезы при наличии односторонней альтернативы.
. Все остальные действия проводятся по той же схеме, что и при проверке гипотезы о значении коэффициента. То же самое можно сказать и о проверке гипотезы при наличии односторонней альтернативы.
Продолжение примера 2.1. На уровне значимости 0,05 проверить гипотезы о значимости коэффициентов регрессии.
Решение. Рассмотрим последовательно решение задачи для каждого из трех коэффициентов.
1. 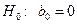 (коэффициент регрессии незначим),
(коэффициент регрессии незначим),
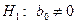 (коэффициент регрессии значим).
(коэффициент регрессии значим).
Расчетное значение 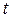 -статистики по формуле (2.8) равно:
-статистики по формуле (2.8) равно: 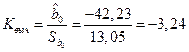 .
.
Критическая значение статистики определяем по табл. 3:
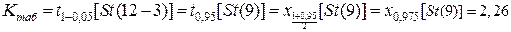 .
.
Поскольку 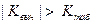 , то гипотезу о значимости параметра регрессии
, то гипотезу о значимости параметра регрессии 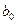 следует принять.
следует принять.
2. 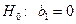 ,
,
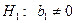 .
.
Расчетное значение 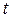 -статистики по формуле (2.8) равно:
-статистики по формуле (2.8) равно: 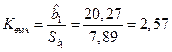 .
.
Критическое значение статистики то же, что и в предыдущем случае. Поскольку 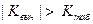 , то параметр модели
, то параметр модели 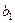 значим на уровне значимости 0,05.
значим на уровне значимости 0,05.
3. 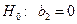 ,
,
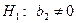 .
.
Расчетное значение 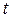 -статистики по формуле (2.8) равно:
-статистики по формуле (2.8) равно: 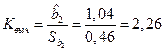 .
.
Поскольку 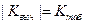 , то гипотезу
, то гипотезу 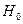 следует принять, т.е. нет оснований отклонить эту гипотезу: параметр регрессии
следует принять, т.е. нет оснований отклонить эту гипотезу: параметр регрессии 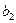 не значим.
не значим.
По коэффициентам регрессии обычно невозможно определить, какой их факторов оказывает наибольшее влияние на зависимую переменную, так как коэффициенты регрессии между собой несопоставимы (они, как правило, имеют различную размерность).
Различие в единицах измерения отсутствуют у частных средних коэффициентов эластичности. Частный коэффициент показывает на сколько процентов в среднем изменяется зависимая переменная с увеличением на 1% определенного фактора 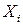 при фиксированном значении других факторов. Его значение рассчитывается по формуле
при фиксированном значении других факторов. Его значение рассчитывается по формуле
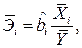 (2.9)
(2.9)
где 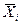 — среднее значение изучаемого фактора
— среднее значение изучаемого фактора 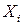 .
.
Сопоставление эффектов влияния на результат различных факторов может быть осуществлено также с помощью стандартизованных коэффициентов регрессии (или бэта — коэффициентов). Бэта-коэффициент 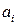 показывает на сколько величин
показывает на сколько величин 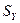 изменится в среднем зависимая переменная
изменится в среднем зависимая переменная 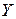 при увеличении только одной
при увеличении только одной 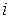 -й объясняющей переменной на
-й объясняющей переменной на 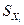 .
.
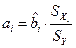 (2.10)
(2.10)
Бэта-коэффициенты определены только для модели со свободным членом (2.2), и конструктивно могут быть найдены с помощью соотношения:
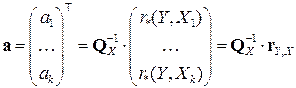 , (2.11)
, (2.11)
в котором 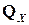 - выборочная корреляционная матрица независимых переменных
- выборочная корреляционная матрица независимых переменных 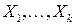 .
.
Бэта-коэффициенты позволяют записать оценку функции множественной линейной регрессии в нормированной форме:
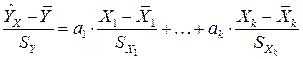 . (2.12)
. (2.12)
Продолжение примера 2.1. Найти частные коэффициенты эластичности и стандартизованные коэффициенты регрессии. Сделайте вывод о силе влияния факторов 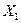 и
и 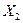 на результирующую переменную
на результирующую переменную 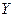 .
.
Решение. Проведем вспомогательные вычисления:
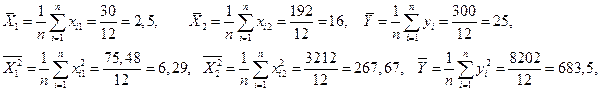
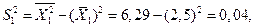
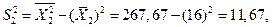
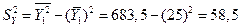 .
.
Найдем частные коэффициенты эластичности (2.9):
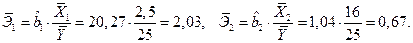
Вывод. При увеличении только количества работающих ( 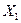 ) на 1% и неизменном
) на 1% и неизменном 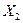 средний объем продаж услуг (
средний объем продаж услуг ( 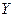 ) увеличится на 2,03%., а при увеличении объема основных производственных средств (
) увеличится на 2,03%., а при увеличении объема основных производственных средств ( 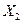 ) на 1% и неизменном
) на 1% и неизменном 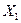 средний объем продаж услуг (
средний объем продаж услуг ( 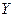 ) увеличится на 0,67%.
) увеличится на 0,67%.
Определим стандартизованные коэффициенты регрессии (2.10):
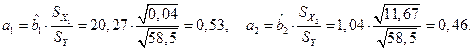
Вывод . При увеличении только количества работающих ( 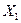 ) на 1 величину
) на 1 величину 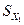 . (при неизменном
. (при неизменном 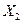 ) средний объем продаж услуг (
) средний объем продаж услуг ( 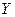 ) увеличится на.0,53 величин
) увеличится на.0,53 величин 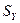 , а при увеличении объема основных производственных средств (
, а при увеличении объема основных производственных средств ( 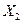 ) на 1 величину
) на 1 величину 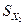 (при неизменном
(при неизменном 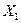 ) средний объем продаж услуг (
) средний объем продаж услуг ( 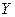 ) увеличится на 0,46 величин
) увеличится на 0,46 величин 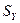 .
.
На основании рассчитанных коэффициентов можно сделать вывод, что величина, характеризующая количество рабочих 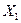 сильнее влияет на объем продаж
сильнее влияет на объем продаж 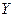 , чем объем основных производственных средств
, чем объем основных производственных средств 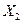 .
.
Дата: 2018-12-28, просмотров: 341.