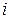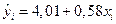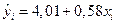Этап оценивания неизвестных коэффициентов модели (1.1) завершается получением оценки уравнения регрессии (1.6). Возникает вопрос о том, насколько хорошо эта оценка соответствует функции регрессии 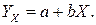 Такую задачу называют проверкой качества найденного уравнения регрессии. Для решения этой проблемы используют в первую очередь такие распространенные статистики, как остатки модели
Такую задачу называют проверкой качества найденного уравнения регрессии. Для решения этой проблемы используют в первую очередь такие распространенные статистики, как остатки модели 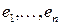 , оценка дисперсии
, оценка дисперсии 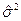 и коэффициент детерминации
и коэффициент детерминации 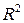 , определяемые выражениями:
, определяемые выражениями:
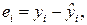 (1.15)
(1.15)
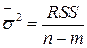
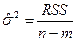 и (1.16)
и (1.16)
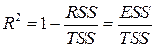 , (1.17)
, (1.17)
где
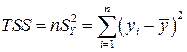 ,
, 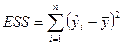 , (1.18)
, (1.18)
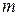 - число параметров модели (в рассматриваемом случае это параметры
- число параметров модели (в рассматриваемом случае это параметры 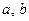 и потому
и потому 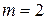 ). Величину
). Величину 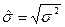 называют стандартной ошибкой модели.
называют стандартной ошибкой модели.
Поскольку для модели (1.2) справедливо тождество 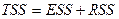 , возможна следующая интерпретация отдельных компонент тождества. Величину
, возможна следующая интерпретация отдельных компонент тождества. Величину 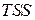 называют полной суммой квадратов (total sum of squares), величину
называют полной суммой квадратов (total sum of squares), величину 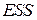 называют суммой квадратов, объясненной моделью (explained sum of squares). Полная сумма квадратов характеризует общую изменчивость зависимой переменной. Величина
называют суммой квадратов, объясненной моделью (explained sum of squares). Полная сумма квадратов характеризует общую изменчивость зависимой переменной. Величина 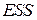 определяют ту часть
определяют ту часть 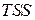 , которую позволяет объяснить предложенная модель, а
, которую позволяет объяснить предложенная модель, а 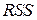 определяет ту часть
определяет ту часть 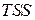 , которую не позволяет объяснить предложенная модель. Соответственно коэффициент детерминации определяет долю дисперсии зависимой переменной, объясненную эмпирической функцией регрессии. По этой причине коэффициент детерминации является основной мерой качества подгонки регрессионной модели к данным с помощью выборочного уравнения регрессии.
, которую не позволяет объяснить предложенная модель. Соответственно коэффициент детерминации определяет долю дисперсии зависимой переменной, объясненную эмпирической функцией регрессии. По этой причине коэффициент детерминации является основной мерой качества подгонки регрессионной модели к данным с помощью выборочного уравнения регрессии.
Замечание 1. Для простейшей парной линейной регрессионной модели (какую мы здесь и рассматриваем), коэффициент детерминации равен квадрату коэффициента корреляции:
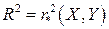 .
.
Чем ближе 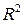 к единице, тем выше качество подгонки зависимой переменной с помощью выбранной регрессионной модели и тем более точно функция
к единице, тем выше качество подгонки зависимой переменной с помощью выбранной регрессионной модели и тем более точно функция 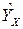 аппроксимирует поведение
аппроксимирует поведение 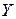 с учетом изменения независимой переменной
с учетом изменения независимой переменной 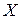 .
.
Замечание 2. Вычисление 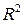 корректно, если константа
корректно, если константа 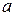 включена в уравнение регрессии.
включена в уравнение регрессии.
Вопрос о том, отличается ли 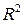 существенно от нуля, решается путем проверки гипотезы о значимости линейной регрессионной модели. При этом проверяется нулевая гипотеза:
существенно от нуля, решается путем проверки гипотезы о значимости линейной регрессионной модели. При этом проверяется нулевая гипотеза: 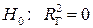 (коэффициент детерминации генеральной совокупности равен нулю, модель регрессии незначима) при конкурирующей гипотезе:
(коэффициент детерминации генеральной совокупности равен нулю, модель регрессии незначима) при конкурирующей гипотезе: 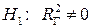 (модель регрессии значима). Проверка значимости модели осуществляется с помощью
(модель регрессии значима). Проверка значимости модели осуществляется с помощью 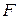 -критерия Фишера.
-критерия Фишера.
Значение 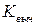 статистики
статистики 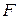 -критерия находится по формуле:
-критерия находится по формуле:
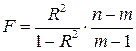 (1.19)
(1.19)
где 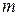 — число параметров модели (1.1). При условии справедливости нулевой гипотезы
— число параметров модели (1.1). При условии справедливости нулевой гипотезы 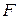 -статистика критерия имеет распределение Фишера с
-статистика критерия имеет распределение Фишера с 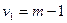 и
и 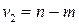 степенями свободы. Критическое значение статистики определяется формулой
степенями свободы. Критическое значение статистики определяется формулой
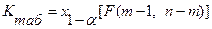 (1.20)
(1.20)
и находится по табл. 5 и 6.
Если 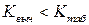 , то гипотезу о незначимости модели
, то гипотезу о незначимости модели 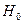 следует принять, т.е. нет оснований отклонить эту гипотезу. Если
следует принять, т.е. нет оснований отклонить эту гипотезу. Если 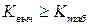 , то гипотезу о значимости
, то гипотезу о значимости 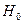 следует отклонить.
следует отклонить.
Продолжение примера 1.1. Определить коэффициент детерминации и сделать вывод о качестве построенной модели. На уровне 0,05 проверить значимость этой модели.
Решение. Для нахождения 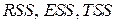 определим
определим 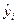 — расчетные значения зависимой переменной. Для удобства промежуточные результаты вычислений поместим в следующую таблицу:
— расчетные значения зависимой переменной. Для удобства промежуточные результаты вычислений поместим в следующую таблицу:
|
| 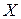
|
| 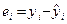
|
| 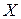
|
| 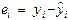
|
| 1 | 16,3 | 13,44 | 1,16 | 16 | 19,1 | 15,06 | 0,04 |
| 2 | 9,2 | 9,33 | 0,67 | 17 | 14,1 | 12,17 | -0,77 |
| 3 | 13,5 | 11,82 | -1,32 | 18 | 21,8 | 16,62 | 0,78 |
| 4 | 16,3 | 13,44 | -1,44 | 19 | 12,5 | 11,24 | 0,06 |
| 5 | 15,6 | 13,04 | -1,14 | 20 | 10,4 | 10,03 | -0,03 |
| 6 | 12,1 | 11,01 | 1,39 | 21 | 20,8 | 16,04 | 0,16 |
| 7 | 16,8 | 13,73 | 1,07 | 22 | 22,7 | 17,14 | 0,46 |
| 8 | 19,3 | 15,18 | 0,52 | 23 | 17,8 | 14,31 | 0,09 |
| 9 | 13,7 | 11,94 | -1,04 | 24 | 10,2 | 9,91 | 0,49 |
| 10 | 15,9 | 13,21 | 1,19 | 25 | 16,0 | 13,27 | -0,17 |
| 11 | 11,9 | 10,90 | 0,10 | 26 | 13,3 | 11,71 | -1,01 |
| 12 | 19,2 | 15,12 | 0,08 | 27 | 19,4 | 15,23 | -0,83 |
| 13 | 18,7 | 14,83 | -0,23 | 28 | 20,9 | 16,10 | 0,00 |
| 14 | 21,5 | 16,45 | -0,05 | 29 | 12,0 | 10,95 | 0,35 |
| 15 | 21,7 | 16,57 | -0,57 | 30 | 16,9 | 13,79 | 0,01 |
Затем последовательно найдем:
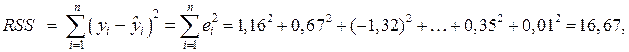
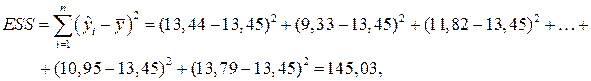
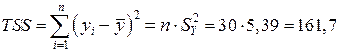 .
.
Как видно, разложение полной суммы квадратов является верным: 161,7=16,67+145,03.
Используя (1.17) найдем коэффициент детерминации:
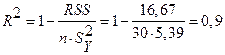 .
.
Коэффициент детерминации может быть найден также с помощью замечания 1:
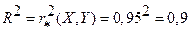 .
.
Вывод: Доля дисперсии зависимой переменной  , объясненная построенной линейной моделью составляет 90%, остальные 10% дисперсии объяснить не удалось.
, объясненная построенной линейной моделью составляет 90%, остальные 10% дисперсии объяснить не удалось.
Проверим гипотезу о значимости модели. Вычислим значение статистики  -критерия по формуле (1.19):
-критерия по формуле (1.19):
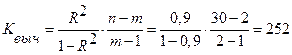 .
.
Критическое значение статистики критерия находим по табл. 6:
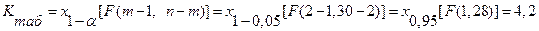 .
.
Так как 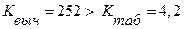 , то гипотезу о незначимости модели
, то гипотезу о незначимости модели 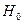 следует отвергнуть, т.е. на уровне значимости 0,05 можно утверждать, что модель, характеризующая зависимость
следует отвергнуть, т.е. на уровне значимости 0,05 можно утверждать, что модель, характеризующая зависимость 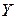 - средней ежегодной прибыли портфеля ценных бумаг от риска портфеля
- средней ежегодной прибыли портфеля ценных бумаг от риска портфеля 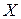 , является значимой.
, является значимой.
Продолжение примера 1.1. Определить оценку дисперсии ошибки модели
Решение. Воспользовавшись (1.16), получим 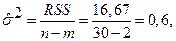 поскольку число параметров модели равно
поскольку число параметров модели равно 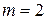 . Стандартная ошибка регрессии равна
. Стандартная ошибка регрессии равна 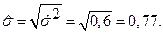
Дата: 2018-12-28, просмотров: 633.