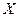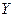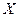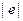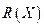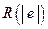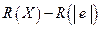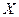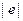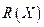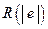Одной из предпосылок регрессионного анализа является предположение о постоянстве дисперсии случайной ошибки для всех наблюдений (свойство гомоскедастичности). Это значит, что для любых значений объясняющих переменных случайные ошибки имеют одинаковые дисперсии. Если это условие не соблюдается, то имеет место гетероскедастичность (heteroscedasticity).. Вместо термина «гетероскедастичная модель» часто используют термин «модель с неравноточными наблюдениями». В случае гетероскедастичной модели МНК-оценки коэффициентов регрессии оказываются хотя и несмещенными, но неэффективными.
Простейший способ обнаружения гетероскедастичности графический, к сожалению, имеет ограниченное применение. Если по оси абсцисс откладывать значения одной из экзогенных переменных при фиксированных остальных, а по оси ординат — соответствующие значения эндогенной переменной, то гетероскедастичность проявляется в существенно различном характере разброса данных около предполагаемой линии регрессии. При одних значениях эндогенной переменной разброс небольшой, а при других значительно больше. Разумеется, что такой «визуальный метод» является достаточно грубым.
Математически обоснованный вывод о гетероскедастичности модели можно получить только с привлечением аппарата проверки гипотез. В качестве основной гипотезы 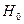 выдвигается гипотеза о равноточности наблюдений (или о гомоскедастичности модели), а в качестве альтернативной гипотезы
выдвигается гипотеза о равноточности наблюдений (или о гомоскедастичности модели), а в качестве альтернативной гипотезы 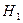 выдвигается гипотеза о гетероскедастичности.
выдвигается гипотеза о гетероскедастичности.
Во всех тестах на гетероскедастичность проверяется нулевая гипотеза 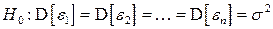 . Наиболее универсальным среди них является тест Уайта (White). Основным его недостатком является то, что он не позволяет определить функциональную форму гетероскедастичности. Аналогичную направленность имеет тест ранговой корреляции Спирмена Для установления конкретной формы гетероскедастичности используются тесты Парка (Park), Глейзера (Glejser), Голдфелда-Куандта (Goldfelf-Quandt), Бреуша-Пагана (Breusch-Pagan).
. Наиболее универсальным среди них является тест Уайта (White). Основным его недостатком является то, что он не позволяет определить функциональную форму гетероскедастичности. Аналогичную направленность имеет тест ранговой корреляции Спирмена Для установления конкретной формы гетероскедастичности используются тесты Парка (Park), Глейзера (Glejser), Голдфелда-Куандта (Goldfelf-Quandt), Бреуша-Пагана (Breusch-Pagan).
Пример 3.2. Исследуется регрессионная зависимость выпуска продукции деревообрабатывающей продукции обрабатывающей промышленности на душу населения 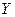 от валового внутреннего продукта на душу населения
от валового внутреннего продукта на душу населения 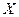 в том же году для 18 стран по исходным данным, приведенным в следующей таблице.
в том же году для 18 стран по исходным данным, приведенным в следующей таблице.
| страна |
|
| страна |
|
|
| 1 | 3 | 18 | 10 | 24 | 100 |
| 2 | 6 | 27 | 11 | 25 | 63 |
| 3 | 7 | 18 | 12 | 26 | 130 |
| 4 | 9 | 45 | 13 | 27 | 135 |
| 5 | 13 | 55 | 14 | 28 | 60 |
| 6 | 15 | 68 | 15 | 35 | 70 |
| 7 | 18 | 51 | 16 | 37 | 80 |
| 8 | 21 | 84 | 17 | 44 | 180 |
| 9 | 22 | 85 | 18 | 48 | 110 |
Используя графический подход сделать вывод о наличии или отсутствии гетероскедастичности в линейной модели.
Решение. Если предположить, что зависимость между переменными 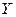 и
и 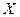 является линейной вида
является линейной вида 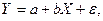 то оценка функции регрессии, найденная по методу наименьших квадратов, имеет вид:
то оценка функции регрессии, найденная по методу наименьших квадратов, имеет вид:
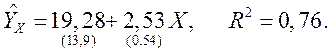
В скобках указаны стандартные ошибки оценок соответствующих коэффициентов регрессии. Корреляционное поле, соответствующее приведенным в таблице данным, приведено на рис 2.
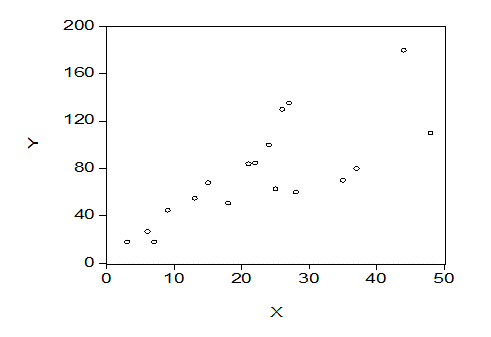
Рис. 2
Анализируя график, можно предположить наличие гетероскедастичности в модели, поскольку. при увеличении значений переменной 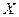 разброс значений переменной
разброс значений переменной 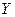 увеличивается.
увеличивается.
Критерий ранговой корреляции Спирмена. Критерий предназначен для обнаружения наличия зависимости значения дисперсии случайной ошибки от значения определенной независимой переменной с использованием рангового подхода.
Ранг элемента выборки — это порядковый номер, под которым это значение располагается в вариационном ряду. Если имеется несколько равных по значению элементов выборки, то их ранг равен среднему значению номеров.
Статистикой критерия ранговой корреляции Спирмена является случайная величина вида
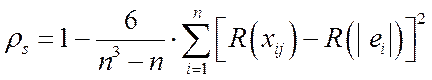 , (3.7)
, (3.7)
где 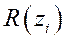 – ранг
– ранг 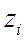 в выборке
в выборке 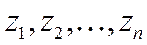 .
.
При достаточно большом объеме выборки гипотеза об отсутствии гетероскедастичности принимается, если выполняется неравенство
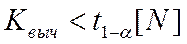 , где
, где 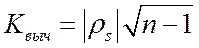 . (3.8)
. (3.8)
Продолжение примера 3.2. На уровне значимости 0,05 проверить гипотезу о гетероскедастичности остатков по тесту Спирмена.
Решение. Проверим гипотезу: 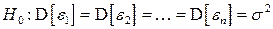 против альтернативной
против альтернативной 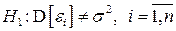 . В следующей таблице приведены данные о значениях переменной
. В следующей таблице приведены данные о значениях переменной 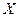 , регрессионных остатков
, регрессионных остатков 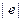 , а также ранги этих величин.
, а также ранги этих величин.
|
|
|
|
|
|
|
|
|
|
|
| 3 | 8,87 | 1 | 4 | -3 | 24 | 20,02 | 10 | 11 | -1 |
| 6 | 7,46 | 2 | 3 | -1 | 25 | 19,51 | 11 | 10 | 1 |
| 7 | 18,99 | 3 | 9 | -6 | 26 | 44,96 | 12 | 16 | -4 |
| 9 | 2,96 | 4 | 2 | 2 | 27 | 47,43 | 13 | 17 | -4 |
| 13 | 2,84 | 5 | 1 | 4 | 28 | 30,10 | 14 | 12 | 2 |
| 15 | 10,78 | 6 | 6 | 0 | 35 | 37,80 | 15 | 15 | 0 |
| 18 | 13,81 | 7 | 8 | -1 | 37 | 32,86 | 16 | 14 | 2 |
| 21 | 11,60 | 8 | 7 | 1 | 44 | 49,43 | 17 | 18 | -1 |
| 22 | 10,08 | 9 | 5 | 4 | 48 | 30,68 | 18 | 13 | 5 |
Таким образом, ранговый коэффициент корреляции Спирмена равен:
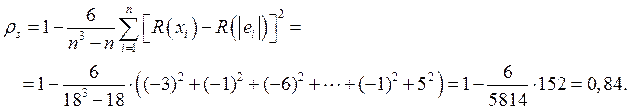
Фактическое значение статистики критерия равно:
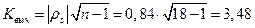 .
.
Критическое значение статистики критерия находим по табл. 2:
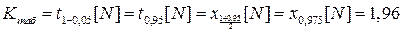 .
.
Поскольку 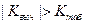 , то гипотезу о гомоскедастичности отвергаем. На уровне значимости 0,05 можно утверждать, что модель гетероскедастична.
, то гипотезу о гомоскедастичности отвергаем. На уровне значимости 0,05 можно утверждать, что модель гетероскедастична.
Дата: 2018-12-28, просмотров: 398.