ВВЕДЕНИЕ
Эконометрика ( Econometrics ) - совокупность методов анализа связей между различными экономическими показателями (факторами) на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики. Применение этих методов позволяет придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. Эконометрические методы могут оказаться полезными и в том случае, когда в распоряжении исследователя нет ясной экономической теории, описывающей поведение интересующих его экономических показателей. В обоих случаях главной целью усилий исследователя является построение экономической модели, адекватной имеющимся данным и существующим положениям экономической теории. Затем построенная модель применяется либо для прогнозирования будущих значений исследуемого показателя, либо для нахождения условий, при которых этот показатель принимает оптимальные значения.
Основные переменные регрессионной модели:
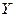- основной экономический показатель, поведение которого изучается (зависимая переменная, эндогенная переменная, отклик);
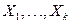- экономические показатели (независимые переменные, экзогенные переменные, факторы), которые оказывают (а возможно и нет, исследователь тоже может ошибаться) влияние на поведение 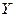; в том случае, когда в модели будет только одна независимая переменная, вместо 
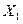в целях упрощения будет использоваться обозначение 
;
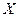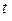- независимая переменная, интерпретируемая как время;
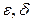- случайные компоненты регрессионной модели (используются для описания эффекта влияния на 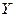тех экономических показателей и внешних обстоятельств, учесть влияние которых не представляется возможным или целесообразным).
Регр ессионная модель и регрессионная функция.
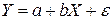- парная линейная регрессионная модель;
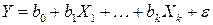- множественная линейная регрессионная модель
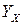- функция регрессии
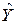- оценка зависимой переменной
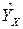- оценка функции регрессии
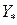- прогнозируемое значение
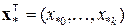- точка прогноза
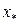- точка прогноза
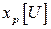- односторонняя квантиль уровня 
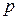распределения случайной величины 
;
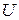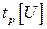- двусторонняя квантиль уровня 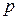распределения случайной величины ;
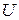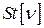- распределение Стьюдента с 
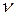степенями свободы;
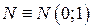- стандартное нормальное распределение;
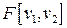— распределение Фишера с 
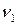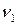и степенями свободы;
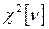— распределение хи-квадрат с 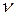степенями свободы.
Наиболее простыми являются парные регрессионные модели, отражающие зависимость одного результативного признака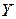 
от одной независимой переменной 
.
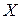Парный регрессионный анализ
Регрессионной модели
Рассмотрим задачу нахождения оценок неизвестных параметров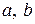 
модели (1.1) по результатам наблюдений 
.
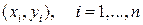Система нормальных уравнений для определения оценок неизвестных параметров линейной регрессии:
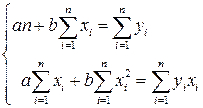(1.3)
Разделив обе части системы (1.3) на n, получим систему нормальных уравнений в виде:
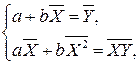(1.4)
где соответствующие средние (means) определяются по формулам:
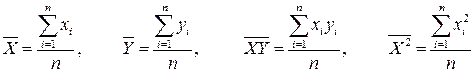
Подставляя значение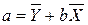 
из первого уравнения (1.4) во второе уравнение, найдем оценки неизвестных параметров регрессии:
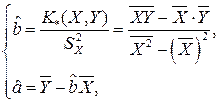(1.5)
где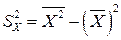 
— выборочная дисперсия (sample variances) переменной 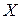, а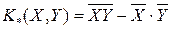 
— выборочная ковариация или выборочный ковариационный момент. Статистики 
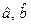называются оценками наименьших квадратов (least squares estimates) неизвестных параметров 
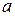и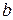 
или LS — оценками.
Оценку функции регрессии (эмпирическую регрессию, выборочную регрессию, уравнение прямой регрессии 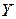по 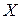) определяют соотношения:
. 
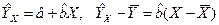(1.6)
Линия регрессии всегда проходит через точку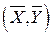 
. Коэффициент 
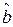— есть угловой коэффициент регрессии. Он показывает, на сколько единиц в среднем изменится переменная 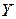при увеличении независимой переменной 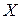на единицу.
Постоянная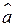 
дает оценку среднего значения зависимой переменной при 
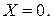Эта интерпретация возможна или невозможна в зависимости от того, насколько далеко находится 
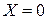от выборочных значений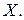 
Используя (1.6) можно найти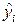 
- оценку значения 
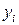по формуле
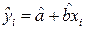. (1.7)
Эти значения позволяют определить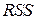 
— минимальное значение суммы квадратов 
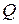в следующем виде
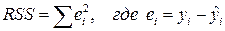. (1.8)
Величину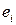 
, появившуюся в (1.8), называют 
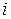-м остатком. В результате наблюдаемые значения 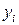можно представить в виде
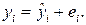(1.9)
Продолжение примера 1.1. Найти МНК-оценки неизвестных параметров линейной регрессионной модели (1.1), описывающей зависимость между средней ежегодной прибылью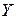 
и среднеквадратичным отклонением 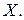Выписать оценку функции регрессии, выражающей эту зависимость. Дать интерпретацию ее коэффициентов.
Решение. Вычислим сначала вспомогательные суммы
,
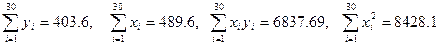а затем необходимые выборочные характеристики
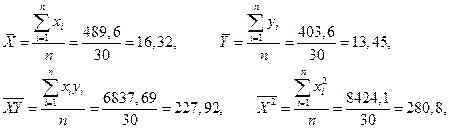
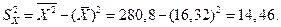
Воспользовавшись формулами (1.5), найдем искомые оценки
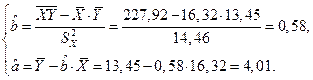
Поэтому уравнение регрессии (1.6) примет вид
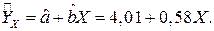
Это означает, что увеличение среднеквадратичного отклонения 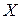на 1% приводит к увеличению ежегодной прибыли по портфелю ценных бумаг в среднем на 0,58%. Если инвестиционный портфель безрисковый, то его прибыль в среднем составит 4,01%
Двусторонней альтернативы
Этот вариант гипотезы используется в том случае, когда отсутствуют априорные сведения о знаке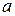 
. На формальном языке решается задача
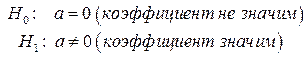. (1.40)
Нулевая гипотеза принимается, если выполняется неравенство
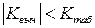. (1.41)
Значение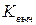 
находится по формуле (1.39), а значение 
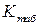- с помощью выражения
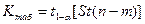, (1.42)
вычисляемого с помощью табл. 3.
Продолжение примера 1.1. На уровне значимости 0,02 проверить гипотезу о значимости коэффициента регрессии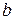 
.
Решение. Проверим гипотезу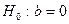 
(коэффициент регрессии не значим) против конкурирующей гипотезы 
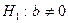(коэффициент регрессии значим). Вычислим значение 
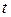-статистики 
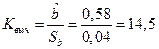. Используя (1.42) по табл. 3, найдем двустороннюю квантиль распределения Стьюдента:
.
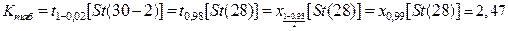Поскольку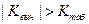 
, то следует принять гипотезу о значимости параметра регрессии 
.
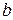ВВЕДЕНИЕ
Эконометрика ( Econometrics ) - совокупность методов анализа связей между различными экономическими показателями (факторами) на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики. Применение этих методов позволяет придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. Эконометрические методы могут оказаться полезными и в том случае, когда в распоряжении исследователя нет ясной экономической теории, описывающей поведение интересующих его экономических показателей. В обоих случаях главной целью усилий исследователя является построение экономической модели, адекватной имеющимся данным и существующим положениям экономической теории. Затем построенная модель применяется либо для прогнозирования будущих значений исследуемого показателя, либо для нахождения условий, при которых этот показатель принимает оптимальные значения.
Основные переменные регрессионной модели:
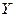- основной экономический показатель, поведение которого изучается (зависимая переменная, эндогенная переменная, отклик);
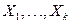- экономические показатели (независимые переменные, экзогенные переменные, факторы), которые оказывают (а возможно и нет, исследователь тоже может ошибаться) влияние на поведение 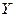; в том случае, когда в модели будет только одна независимая переменная, вместо 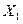в целях упрощения будет использоваться обозначение ;
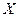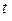- независимая переменная, интерпретируемая как время;
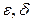- случайные компоненты регрессионной модели (используются для описания эффекта влияния на 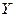тех экономических показателей и внешних обстоятельств, учесть влияние которых не представляется возможным или целесообразным).
Регр ессионная модель и регрессионная функция.
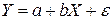- парная линейная регрессионная модель;
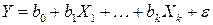- множественная линейная регрессионная модель
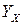- функция регрессии
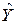- оценка зависимой переменной
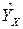- оценка функции регрессии
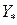- прогнозируемое значение
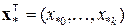- точка прогноза
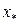- точка прогноза
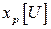- односторонняя квантиль уровня 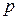распределения случайной величины ;
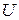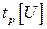- двусторонняя квантиль уровня 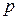распределения случайной величины ;
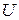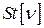- распределение Стьюдента с 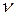степенями свободы;
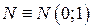- стандартное нормальное распределение;
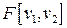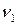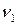— распределение Фишера с и степенями свободы;
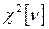— распределение хи-квадрат с 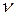степенями свободы.
Наиболее простыми являются парные регрессионные модели, отражающие зависимость одного результативного признака 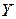от одной независимой переменной .
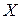Парный регрессионный анализ
Парная линейная регрессионная модель. Выбор модели
В модели парной линейной регрессии зависимость между переменным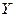и и 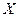представляется в виде
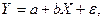(1.1)
где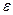 
- случайная ошибка модели (error, или disturbance). Постоянные 
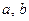— неизвестные параметры модели. Наличие случайного члена 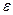связано с воздействием на зависимую переменную 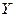других факторов, неучтенных в функции регрессии, с возможной нелинейностью модели и ошибками измерения. В данной модели функция регрессии является линейной функцией: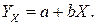 
Выбор линейной модели обычно обуславливается либо содержательными, либо геометрическими соображениями. Использование геометрических соображений заключается в том, что результаты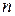 
наблюдений 
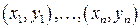переменных 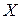и 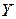изображаются в виде точек в декартовой системе координат. Получаемое таким образом изображение получило название диаграммы рассеяния или корреляционного поля наблюдений. Пример такого изображения можно найти на рис.1.
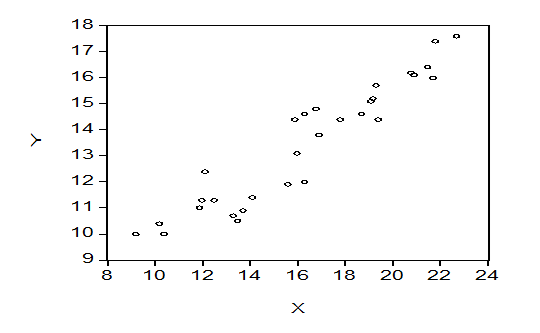
Рис. 1
По расположению точек на рис.1 можно предположить наличие линейной регрессионной зависимости между признаками 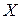и .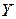
Пример 1.1. Сделать вывод о характере зависимости между 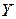- средней ежегодной прибылью (в %) портфеля ценных бумаг и его риском, измеряемым с помощью среднеквадратичного отклонения прибыли 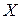(в %) по отчетам о деятельности 30 инвестиционных фондов США за период с 1954 по 1963 гг. [1]. Необходимые сведения о деятельности фондов приведены в следующей таблице:
|
|
|
|
|
|
|
| 1 | 14,6 | 16,3 | 16 | 15,1 | 19,1 |
| 2 | 10 | 9,2 | 17 | 11,4 | 14,1 |
| 3 | 10,5 | 13,5 | 18 | 17,4 | 21,8 |
| 4 | 12,0 | 16,3 | 19 | 11,3 | 12,5 |
| 5 | 11,9 | 15,6 | 20 | 10,0 | 10,4 |
| 6 | 12,4 | 12,1 | 21 | 16,2 | 20,8 |
| 7 | 14,8 | 16,8 | 22 | 17,6 | 22,7 |
| 8 | 15,7 | 19,3 | 23 | 14,4 | 17,8 |
| 9 | 10,9 | 13,7 | 24 | 10,4 | 10,2 |
| 10 | 14,4 | 15,9 | 25 | 13,1 | 16,0 |
| 11 | 11,0 | 11,9 | 26 | 10,7 | 13,3 |
| 12 | 15,2 | 19,2 | 27 | 14,4 | 19,4 |
| 13 | 14,6 | 18,7 | 28 | 16,1 | 20,9 |
| 14 | 16,4 | 21,5 | 29 | 11,3 | 12,0 |
| 15 | 16,0 | 21,7 | 30 | 13,8 | 16,9 |
Решение. Корреляционное поле наблюдений, соответствующее приведенным в таблице данным, приведено на рис 1. Как можно судить по графику, все точки расположены вблизи некоторой мыслимой прямой, что дает основание предположить линейный характер регрессионной зависимости между переменными. Это предположение соответствует одному из положений модели оценки финансовых активов САРМ о линейном характере зависимости между средней ежегодной прибылью портфеля ценных бумаг и ее среднеквадратичным отклонением. Учитывая также, что амплитуда колебаний прибыли 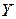практически не меняется при ее росте, имеются веские основания описать зависимость между переменным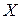и и 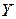с помощью модели (1.1).
Дата: 2018-12-28, просмотров: 264.
