При работе с реальными статистическими данными важно проверить, действительно ли желаемые ограничения (условия, определяющие классическую парную линейную регрессионную модель) имеют место. После проведения этой проверки может также возникнуть вопрос, как поступить, если выяснится, что нарушение условий действительно имеет место?
Для проверки выполнения стандартных предположений о линейной модели наблюдений помимо графических существует довольно много процедур, использующих статистические критерии проверки гипотез.
Основу тестов, ориентированных на проверку классических предположений, составляют остатки 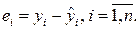 Если все они выполнены, число наблюдений достаточно велико, то, как правило, остатки ведут себя как слабо коррелированные случайные величины, имеющие нормальный закон распределения с нулевым математическим ожиданием и дисперсией
Если все они выполнены, число наблюдений достаточно велико, то, как правило, остатки ведут себя как слабо коррелированные случайные величины, имеющие нормальный закон распределения с нулевым математическим ожиданием и дисперсией 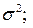 при этом
при этом 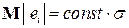 .
.
Начало исследования разумно начать с построения графика временного ряда остатков 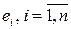 в зависимости от номера наблюдения
в зависимости от номера наблюдения  В благоприятном случае точки временного ряда должны лежать в горизонтальной полосе постоянной ширины. Но такая картина наблюдается лишь в идеальном случае. Поэтому для решения этой проблемы существует набор формальных тестов, каждый из которых ориентирован на решение определенной задачи. Рассмотрим некоторые из них.
В благоприятном случае точки временного ряда должны лежать в горизонтальной полосе постоянной ширины. Но такая картина наблюдается лишь в идеальном случае. Поэтому для решения этой проблемы существует набор формальных тестов, каждый из которых ориентирован на решение определенной задачи. Рассмотрим некоторые из них.
Одно из предположений регрессионного анализа состоит в независимости результатов различных наблюдений, а именно 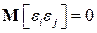 при
при 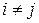 .
.
Если данное условие не выполняется, то говорят, что случайный член подвержен автокорреляции (autocorrelation, serial correlation). В этом случае коэффициенты регрессии, получаемые по МНК, оказываются неэффективными, хотя и несмещенными, а их стандартные ошибки рассчитываются некорректно (занижаются).
Автокорреляция в регрессионном анализе обычно встречается при использовании данных временного типа.
Простейшей моделью автокорреляции ошибок является модель авторегрессии первого порядка:
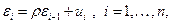
где 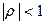 , а
, а 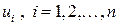 — независимые в совокупности случайные величины, имеющие одно и тоже нормальное распределение
— независимые в совокупности случайные величины, имеющие одно и тоже нормальное распределение 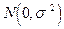 .
.
В таком случае 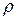 — коэффициент корреляции между двумя случайными соседними членами
— коэффициент корреляции между двумя случайными соседними членами 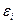 и
и 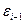 (коэффициент автокорреляции первого порядка):
(коэффициент автокорреляции первого порядка):
· если 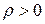 , то автокорреляция положительная;
, то автокорреляция положительная;
· если 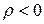 , то автокорреляция отрицательная;
, то автокорреляция отрицательная;
· если 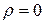 то автокорреляция отсутствует.
то автокорреляция отсутствует.
Поскольку значения случайных ошибок 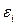 неизвестны, то проверяется статистическая некоррелированность остатков
неизвестны, то проверяется статистическая некоррелированность остатков 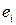 и
и 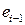 . Статистической оценкой коэффициента корреляции
. Статистической оценкой коэффициента корреляции 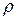 является коэффициент автокорреляции остатков первого порядка
является коэффициент автокорреляции остатков первого порядка
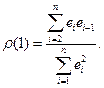 (3.3)
(3.3)
Существует два наиболее распространенных метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.
Второй метод - наиболее простой и достаточно надежный способ определения автокорреляции возмущений (остатков) – использование критерия Дарбина – Уотсона.
Выдвигается нулевая гипотеза об отсутствии автокорреляции первого порядка, т.е. 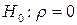 . В качестве альтернативной гипотезы может выступать либо
. В качестве альтернативной гипотезы может выступать либо  (есть автокорреляция), либо
(есть автокорреляция), либо 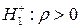 (автокорреляция положительна), либо
(автокорреляция положительна), либо 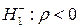 (автокорреляция отрицательна). Для проверки нулевой гипотезы используют статистику Дарбина-Уотсона
(автокорреляция отрицательна). Для проверки нулевой гипотезы используют статистику Дарбина-Уотсона
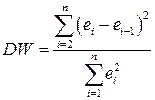 . (3.4)
. (3.4)
Можно показать, что с ростом объема выборки 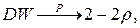 где
где 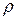 - коэффициент автокорреляции первого порядка последовательности случайных ошибок
- коэффициент автокорреляции первого порядка последовательности случайных ошибок 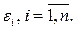
Если автокорреляция остатков отсутствует, то 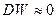 . При положительной автокорреляции имеем
. При положительной автокорреляции имеем 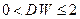 , а при отрицательной - соответственно
, а при отрицательной - соответственно 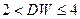 .
.
Проверка гипотезы осуществляется с помощью табл. 8, содержащей критические значения критерия Дарбина-Уотсона 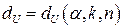 и
и 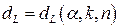 , определяемые по значениям входных параметров
, определяемые по значениям входных параметров 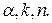
При проверке гипотезы 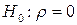 против гипотезы
против гипотезы 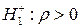 гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство
гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство 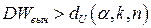 ; гипотеза отклоняется в пользу альтернативной, если
; гипотеза отклоняется в пользу альтернативной, если 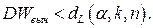
При проверке гипотезы 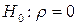 против гипотезы
против гипотезы 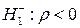 гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство
гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство 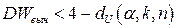 ; гипотеза отклоняется в пользу альтернативной, если
; гипотеза отклоняется в пользу альтернативной, если 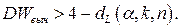
При проверке гипотезы 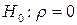 против гипотезы
против гипотезы 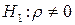 гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство
гипотеза об отсутствии автокорреляции первого порядка принимается, если выполняется неравенство 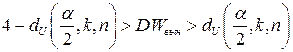 ; гипотеза отклоняется в пользу альтернативной, если
; гипотеза отклоняется в пользу альтернативной, если 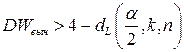 или
или 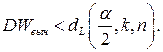
Недостатком критерия Дарбина-Уотсона является наличие области неопределенности критерия, не позволяющей при определенных значениях статистики Дарбина-Уотсона решить задачу проверки гипотез. Наличие области неопределенности критерия обусловлено тем, что распределение статистики зависит не только от числа наблюдений и числа объясняющих переменных, но и от значений объясняющих переменных. Кроме того следует иметь в виду, что критические значения статистики 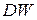 определены для объемов выборки не менее 15.
определены для объемов выборки не менее 15.
Пример 3.1. На основе помесячных данных о количестве разводов (тыс.) в регионе была построена модель временного ряда: 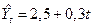 . В таблице указаны остатки множественной линейной регрессионной модели:
. В таблице указаны остатки множественной линейной регрессионной модели:
| Месяц | Остатки | Месяц | Остатки | Месяц | Остатки |
| Январь | -1,0 | Май | -2,0 | Сентябрь | 2,5 |
| Февраль | 2,0 | Июнь | -1,1 | Октябрь | 1,0 |
| Март | -0,5 | Июль | 3,0 | Ноябрь | -3,0 |
| Апрель | 0,5 | Август | 1,0 | Декабрь | 2,0 |
Вычислить коэффициент автокорреляции и проверить гипотезу об автокорреляции ошибок с помощью критерия Дарбина-Уотсона на уровне значимости 0,05.
Решение. Для нахождения коэффициента автокорреляции воспользуемся (3.3):
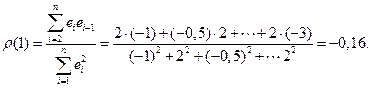
Такое значение коэффициента автокорреляции говорит о достаточно слабой зависимости между остатками 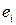 и
и 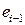 .
.
Выдвигается нулевая гипотеза об отсутствии автокорреляции первого порядка, т.е. 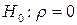 .
.
Дата: 2018-12-28, просмотров: 366.