Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Уравнение гармонических колебаний колебательной величины s: s=Acos(ω₀t+φ) или s=Asin(ω₀t+φ), где A – амплитуда колебаний, ω₀ – круговая (циклическая) частота, φ – начальная фаза колебаний в момент времени t=0, (ω₀t+φ) – фаза колебаний в момент времени t. Рассмотрим уравнение, описывающее колебания, совершаемые системой в отсутствие сил трения 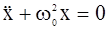. .Итак, смещение X изменяется со временем по закону косинуса. Следовательно, движение механической системы, находящейся под действием квазиупругой силы, представляет собой гармоническое движение.

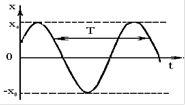
Таким образом мы убедились в том, что под действием квазиупругой силы при малых отклонениях от положения равновесия, частица будет совершать гармонические колебания. На рисунке приведена зависимость смещения частицы от времени. По горизонтальной оси отложено время t, по вертикальной - смещение x. Так как косинус изменяется от -1 до +1, значения x лежат в пределах от -x0 до +x0. Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда x0 - постоянная положительная величина. Величина 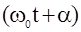, стоящая под знаком косинуса, называется фазой колебания. Постоянная a представляет собой значение фазы в момент t=0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета времени.

Поскольку косинус - периодическая функция с периодом 2π, различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение. Этот промежуток времени называется периодом колебания. 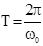 . Число колебаний в единицу времени называется частотой колебаний. Очевидно, что частота связана с периодом колебаний соотношением

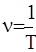 . Из определения периода следует, что 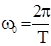. Величину называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой системы. 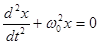- однородное дифференциальное уравнение 2 ого порядка,решением которого является функция вида . .

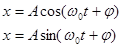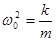Энергия гармонических колебаний.

Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энерги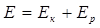и , или 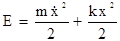           Учитывая, что 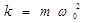и, подставив выражения для X и 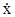, получим .

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу являются консервативными, то ее механическая энергия остается постоянной . В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно. 

 

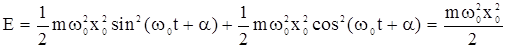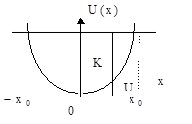
На рисунке приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. М аксимального значения потенциальная энергия достигает в поворотных точках 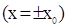, при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.