Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

    Трением качения называется сопротивление, возникающее при  качении одного тела по поверхности другого.

Приложим к оси катка радиуса R и веса P силу Q.  Интенсивность      давлений катка на край А  площадки  АВ убывает, а на край В возрастает    (рис.55).

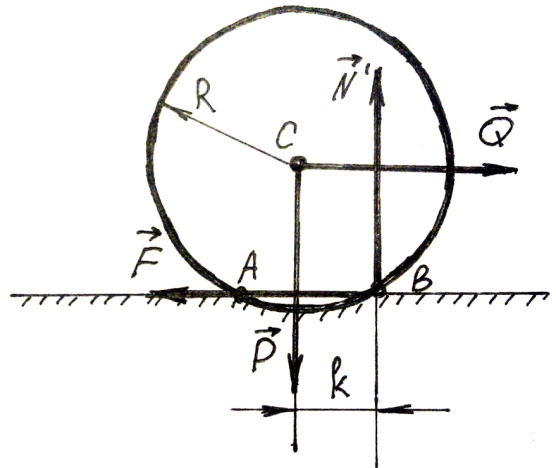
                                                       Рис.55

В результате реакция N  оказывается смещенной в сторону действия силы Q. С увеличением Q это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара (Q , F) с моментом  Q ∙ R  и уравновешивающая ее пара (N, P) с моментом  N k. Из равенства моментов находим Q R=  N k   или

 Q =  N k ∕ R . k – называется  коэффициентом трения качения.

Измеряют  k обычно в сантиметрах. Отношение k ∕ R для большинства материалов значительно меньше коэффициента трения f. Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, подшипники).

 

 

Примеры решения задач на равновесие

Пример на равновесие произвольной плоской системы сил

Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н·м; расстояние a = 1 м.(рис.56).

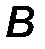
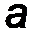
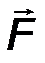
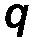
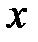
Рис.56

 Дано: F = 60 Н, q = 15 Н/м, М = 40 Н·м, a = 1 м.

     Определить: реакции неподвижного цилиндрического шарнира А и подвижного цилиндрического шарнира В.

Решение

1. Для определения опорных реакций рассмотрим равновесие балки АВ.

   2. К балке АВ приложены активные силы: F, пара сил с моментом М и равномерно распределенная нагрузка интенсивностью q. Заменим распределенную нагрузку эквивалентной сосредоточенной Q, равной по модулю Q = q·2a = 30 Н и приложенной в средней точке нагруженного участка.

Введем декартову систему координат Аxy, совместив начало координат  с неподвижным шарниром А и направив ось Аx вдоль балки.

На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями. Реакция R _A неизвестна по величине и направлению, поэтому разложим её на две неизвестные по величине составляющие X_A, Y_A, направленные по координатным осям. Опора в точке В не препятствует её перемещению вдоль наклонной плоскости и, следовательно, реакцию 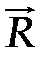_B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине (рис.57).

3.Имеем произвольную плоскую систему сил.

 4. В задаче имеется три неизвестных скалярных величины: X_A, Y_A, R_B. Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой[4].

 

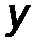
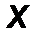
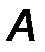
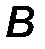
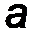
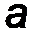
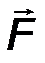
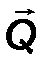
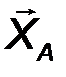
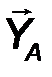
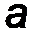
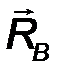
Рис.57

 

Составим уравнения равновесия для полученной эквивалентной силовой схемы.

Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:

 

∑ X = 0,              X _a – R _b sin 30° = 0;                                         (1)

∑ Y = 0,           Y _a – Q + F + R _b cos 30° = 0;                       (2)

∑mom_A F = 0,     -Q∙ a + F ∙2a + M + (R _b cos 30°) ∙ 3a = 0. (3)

Напомним, что скалярные моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции R _b относительно точки А выделена её вертикальная составляющая, равная R _b cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.

Из третьего уравнения (2) и (3) находим:

 

R_B = (Q - 2F - M/a)/(3cos 30°) -50.0 Н .

 

Подставив в первое и второе, получим:

Х _A =((Q - 2F - M/a)/(3cos 30°))sin30° -25.0 Н ,

Y_A = (2 Q - F + M / a )/3 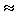13,3 Н.

 

Полученные отрицательные значения R_B и X_A означают, что сила R _b и составляющая реакции X_A противоположны показанным на рис.57 направлениям этих векторов.

Величина реакции R_A = (X_A² + Y_A²) 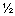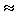28.3 Н.

 

 

Пример на равновесие произвольной пространственной системы сил

 

 

Горизонтальная прямоугольная плита весом Р (рис.58) закреплена с помощью сферического в точке А, цилиндрического шарнира в точке В и

невесомого шарнирно опертого стержня ДД 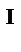 . На плиту в плоскости параллельной плоскости xz, действует сила F, а в плоскости, параллельной yz, - пара сил с моментом М.

 

 

 Дано: Р = 3 кН,  F = 8 кН, М = 4 кН ∙ м, 

ά = 60° , АС = 0,8 м, АВ = 1,2 м,

            ВЕ = 0,4 м, ЕН = 0,4 м.

                    

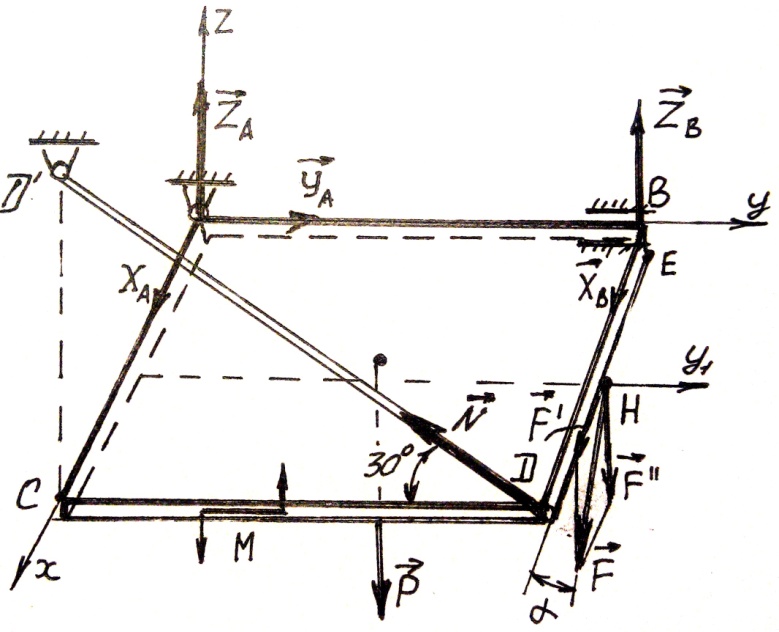
Определить: реакции опор А, В и стержня ДД .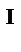

 

 

Рис.58

 

 

               

 

Решение.

1. Рассмотрим равновесие плиты АВДС.

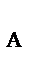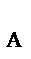2. На плиту действуют активные силы: Р,  F и пара сил с моментом М, а также реакции связей. Реакцию неподвижного сферического шарнира разложим на три составляющие  X , Y , Z 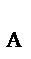, неподвижного цилиндрического шарнира – на две составляющие X 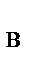, Z 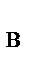 (в плоскости, перпендикулярной оси шарнира); реакцию N стержня направляем вдоль стержня от Д к Д 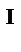, предполагая, что он растянут.

3. Имеем произвольную пространственную систему сил.

 

4. Составим уравнения равновесия для полученной эквивалентной силовой схемы.

Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:

 ∑ X = 0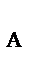, X + X 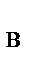+ F cos 60° = 0;

 ∑ Y = 0, Y 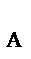− N cos 30° = 0;

  ∑ Z = 0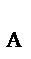.  Z + Z 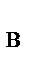 − Р + N sin 30° − F sin 60° = 0;

∑ mom 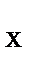F = 0, М − Р ∙АВ/2 + Z 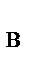∙ АВ − F sin 60° ∙ АВ + N sin 30° ∙ АВ = 0;     

∑ mom 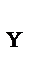F = 0, Р ∙АС/2 + F sin 60° ∙ЕН − N sin 30° ∑АС − F cos 60° ∙ВЕ = 0;

∑ mom 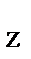F = 0, −X 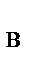∙АВ − N cos 30° ∙АС − F cos 60° ∙АВ = 0.

Подставив в составленные уравнения числовые значения всех заданных

 величин и решив эти уравнения, найдем искомые реакции: X 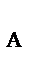= 3,42 кН; Y 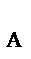= 5,13 кН; Z 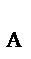= 4,83 кН; X 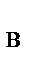= −7,42 кН; Z 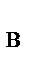= 2,13 кН; N = 5,93кН. Знак «−» указывает на то, что реакция  X  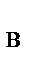направлена противоположно показанной на рис.58.

 

   Список использованной литературы

1.Ишлинский А.Ю.Задачи механики. Препринт №185.М.:Ист-т пробл. Механики АН СССР, 1981.-38 с.

2.Конспект лекций по теоретической механике: Учебное пособие /В.А.Аршинова, А.И.Зайцев – Яросл. гос. ун-т. – Ярославль, 1998.- 176 с.:ил.- (Высшее образование).

3.Теоретическая механика: учебник /Н.Г.Васько, В.А.Волосухин, А.Н.Кабельков, А.Н.Бурцева – Ростов н/Д: Феникс,2012. – 302 с.:ил.- (Высшее образование).

4.Леготин С.Д. Основы теоретической механики: электронный учебник /М. Гос. Индустриальный ун-т, 2008.-136 с.:ил.-(Высшее образование).

 

За помощь при создании данного пособия выражается благодарность студентам машиностроительного факультета Аджояну М.Р и Выборнову Н.С.

[1] Единицей измерения силы в системе единиц СИ является Ньютон (Н); применяется и более крупная единица 1 кН=1000Н.

[2] Ортом вектора называется единичный вектор, направленный в ту же сторону и приложенный в той же точке, что и заданный вектор.

[3] Это следствие, также как и часть аксиом и теорем статики, применимо только для абсолютно твердого, не деформируемого тела.

[4] статически определимой задача статики называется, если число неизвестных компонентов реакций равно числу уравнений равновесия, и наоборот, задача статики называется статически неопределимой, если число неизвестных компонентов реакций больше числа уравнений равновесия.