СТАТИКА
Электронный учебник по дисциплине: ”Теоретическая механика”
для студентов заочной формы обучения
Соответствует Федеральному образовательному стандарту
(третьего поколения)
Сидоров В.Н.,д.т.н.,профессор
Ярославский государственный технический университет
Ярославль, 2014
СОДЕРЖАНИЕ
Введение …………………………………………………………………... 4
1.Основные понятия и определения статики ………………………........ 5
2.Аксиомы статики ……………………………………………………….. 9
3.Основные операции с силами в статике …………………..................... 14
3.1. Операции с силами в плоской (двухмерной) статике ………........ 15
Проекция силы на ось ………………………………………………15
Скалярный момент силы относительно точки ……………………16
Скалярный момент пары сил ………………………………………17
3.2. Операции с силами в пространственной (трехмерной) статике …20
Проекция силы на плоскость ……………………………………...20
Момент силы относительно точки ………………………………..22
Момент силы относительно оси …………………………………..23
Моменты силы относительно координатных осей ………………23
Момент пары сил …………………………………………………..24
4. Связи и реакции связей ………………………………………………...27
5. Произвольная пространственная система сил ………………………..33
5.1. Главный вектор и главный момент
произвольной пространственной системы сил …………………..33
5.2. Теорема о приведении произвольной
пространственной системы сил ………………………………..35
5.3. Инварианты произвольной пространственной
системы сил …………………………………………………….36
5.4. Частные случаи приведения произвольной
пространственной системы сил ……………………………….37
5.5. Алгоритм решения задач на приведение произвольной
пространственной системы сил к простейшему виду ……….41
5.6. Условия равновесия произвольной пространственной
системы сил …………………………………………………….42
6. Вывод условий равновесия различных систем сил из условий
равновесия произвольной пространственной системы сил ………..43
6.1. Условия равновесия плоской системы сил ……………………...44
6.2. Условия равновесия системы параллельных сил ……………….45
6.3. Условия равновесия системы сходящихся сил ………………...45
7. Алгоритм решения задач по статике на равновесие систем сил ….47
8. Замена распределенных сил эквивалентными
сосредоточенными силами …………………………………………47
9. Теорема о зависимости между главными моментами системы
сил относительно двух точек …………………………………….…50
10. Теорема Вариньона для системы сходящихся сил ……………....50
11. Центр системы параллельных сил и центр тяжести …………..…50
11.1. Центр системы параллельных сил ………………………….....50
11.2. Определение положения центра тяжести тела …………….....52
11.3. Методы определения центра тяжести ………………………...54
12. Равновесие тел при наличии трения .................................................57
12.1. Равновесие твердого тела при наличии трения скольжения ...57
12.2. Равновесие твердого тела при наличии трения качения …....58
13. Примеры решения задач на равновесие……………………….…59
Введение
«Кто не знаком с законами механики
тот не может познать природы»
Галилео Галилей
Значение механики, ее значительная роль в совершенствовании производства, повышении его эффективности, ускорении научно-технического процесса и внедрении научных разработок, росте производительности труда и улучшении качества выпускаемой продукции, к сожалению, понимается достаточно отчетливо не всеми руководителями министерств и ведомств, высших учебных заведений, равно как и то, что представляет механика наших дней /1/. Как правило, о ней судят по содержанию теоретической механики, изучаемой во всех высших технических учебных заведениях.
Студенты должны знать, насколько важна теоретическая механика, как одна из основополагающих инженерных дисциплин высшей школы, научная основа важнейших разделов современной техники, своеобразный мост, соединяющий математику и физику с прикладными науками, с будущей профессией. На занятиях по теоретической механике впервые студентам прививается системное мышление, умение ставить и решать практические задачи. Решать их до конца, до числового результата. Учиться анализировать решение, устанавливать границы его применимости и требование к точности исходных данных.
Не менее важно знать студентам, что теоретическая механика лишь вводная, хотя и совершенно необходимая, часть колоссального здания современной механики в широком понимании этой фундаментальной науки. Что она будет развиваться в других разделах механики: сопротивлении материалов, теории пластин и оболочек, теории колебаний, регулирования и устойчивости, кинематике и динамики машин и механизмов, механике жидкости и газа, химической механике.
Достижения всех разделов машиностроения и приборостроения, строительной индустрии и гидротехники, добычи и переработки руды, каменного угля, нефти и газа, железнодорожного и автомобильного транспорта, судостроения, авиации и космической техники опираются на глубокое понимание законов механики.
При подготовке лекций автором использованы методические разработки кафедры теоретической механики Ярославского государственного технического университета /2/ и других известных университетов /3, 4/.
Учебное пособие предназначено для студентов машиностроительных, автомеханических специальностей заочной формы обучения в техническом университете по сокращенной программе курса.
Итак, несколько определений.
Теоретическая механика – это наука, изучающая общие законы механического движения и равновесия материальных объектов и возникающие при этом механические взаимодействия между материальными объектами.
Под механическим движением материального объекта понимают происходящее с течением времени изменение его положения по отношению к другим материальным объектам.
Под механическим взаимодействием подразумевают такие действия тел друг на друга, при которых изменяются движения этих тел, либо они сами деформируются (меняют свою форму).
Теоретическая механика состоит из трех разделов: статики, кинематики и динамики.
Статика – рассматривает два основных вопроса:
а) сложение сил и приведение системы сил к простейшему виду;
б) определение необходимых и достаточных условий равновесия, действующих на абсолютно твердое тело систем сил.
Кинематика - изучает различные движения материальных точек, абсолютно твердых тел и механических систем, но не рассматриваются причины, вызывающие изменение характера движения.
Динамика - рассматривает влияние сил на состояние движения материальных точек, абсолютно твердых тел и механических систем.
1. Основные понятия и определения статики
1.Материальное тело – некоторое количество вещества, заполняющее определенный объем.
2.Материальная точка – тело, имеющее конечную массу, но размерами которого можно пренебречь по сравнению с расстояниями до других тел.
3. Масса – мера инертности тела и его гравитационных свойств.
4.Абсолютно твердое тело – тело, расстояния между любыми точками которого не изменяются с течением времени..
Из последнего определения вытекает, что такое тело – не деформируемое (абсолютно жесткое). Сама же механика – классическая (не релятивистская) механика, т.е. механика, в которой тела движутся со скоростями, существенно меньшими скорости света.
5.Свободная материальная точка (или тело) – такая, на перемещение которой не наложено никаких ограничений. Если перемещение материальной точки (или тела) в пространстве ограничивается другими телами, то ее называют несвободной или связанной . Тела, ограничивающие движение тела, называют связями.
6.Изолированная материальная точка (или тело) – такая, на которую не действуют никакие другие тела.
7.Сила есть мера механического воздействия одного тела на другое. Она характеризует величину и направление этого взаимодействия.
Силу (от английского слова “Force”) принято обозначать большой латинской буквой F, либо другой буквой.
Сила - вектор, при обозначении которого необходимо указывать признаки векторной величины, т.е. указывать надстрочную стрелку, либо саму букву выделять жирным шрифтом F  F.
F.
Указанные здесь обозначения силы эквивалентны, поэтому они объединены символом тождественности «  », или эквивалентности «
», или эквивалентности « 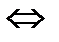 ».
».
Действие силы на тело определяется:
· модулем или абсолютным значением силы (обозначается | F|  F) – это величина силы, выраженная в неких единицах измерения[1];
F) – это величина силы, выраженная в неких единицах измерения[1];
· направлением силы (ортом[2] e);
· точкой приложения силы (т. A).
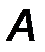
|
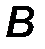
|

|
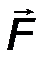
|
Рис.1
Прямая, вдоль которой направлена сила, называется линией действия силы (линия AB, рис.1).
Сила может быть задана:
- геометрическим способом, то есть как вектор с известным модулем F и известным направлением, определяемым ортом e;
- аналитическим способом, то есть её проекциями FX, FY, FZ на оси выбранной системы координат 0xyz .
Проекции силы определяются её модулем и углами α, β и γ, которые образует сила с координатными осями 0x, 0y, 0z, следующими соотношениями:
Fx = F cos α, Fy = cos β, F z = F z cos γ. (1)
Проекция силы на ось равна произведению модуля силы на косинус угла между этой силой и осью.
Модуль силы определяется через свои проекции (рис.2), как:
F = √ F 2 x + F2 y + F2 z . (2)

|
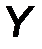
|
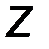
|
|
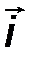
|
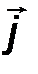
|
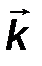
|
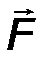
|
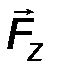
|
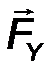
|
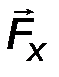
|
Рис.2
Материальные тела могут действовать друг на друга путем непосредственного соприкосновения или на расстоянии. В зависимости от этого силы можно разделить на поверхностные силы, приложенные к поверхности тела (например, силы давления на тело со стороны окружающей среды) и объемные силы, приложенные к данной части тела (например, силы тяготения).
Поверхностные и объемные силы называют распределенными силами. В ряде случаев силы можно рассматривать распределенными по некоторой кривой (например, т.н. «погонный вес», или вес одного метра длины тонкого стержня). Распределенные силы характеризуются их интенсивностью, то есть величиной силы, приходящейся на единицу длины, площади или объема. Интенсивность может быть постоянной (равномерно распределенные силы) или переменной величиной (см. раздел 8).
Если можно пренебречь малыми размерами области действия распределенных сил, то рассматривают сосредоточенную силу, приложенную к телу в одной точке (условное понятие, так как практически приложить силу к одной точке тела нельзя).
Таким образом, можно сформулировать следующую классификацию сил по степени их локализации:
· сосредоточенные силы;
· распределенные силы, в том числе:
- линейно распределенные;
- поверхностные;
- объемные.
По принадлежности к рассматриваемой механической системе силы можно разделить на внешние и внутренние.
Внешними называются силы, которые действуют на это тело (систему) со стороны других тел, внутренними - силы, с которыми части данного тела (данной системы) взаимодействуют друг с другом.
7.Системой сил называют совокупность сил F 1 , F 2 ,… Fn , приложенных к определенному телу (рис.3).
В зависимости от расположения линий действия сил систему сил называют:
· плоской, если линии действия всех сил лежат в одной плоскости;
· пространственной, если линии действия сил не лежат в одной плоскости;
· системой сходящихся сил, если линии действия всех сил пересекаются в одной точке;
· системой параллельных сил, если линии действия всех сил параллельны друг другу.
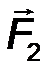
|
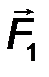
|
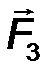
|
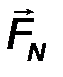
|

|
Рис.3
8. Две системы сил называются эквивалентными, если при замене одной системы сил, приложенных к свободному твердому телу, другой системой сил кинематическое состояние тела не изменится.
Замечание. Если каждая из двух систем сил порознь эквивалентны третьей, то эти две системы эквивалентны между собой.
S 
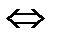 S
S  ; S
; S 
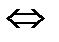 S
S 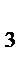 ;
;  S
S 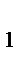
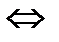 S
S  .
.
9. Система сил называется уравновешенной или эквивалентной нулю, если в результате её приложения кинематическое состояние абсолютно твердого тела не изменится S 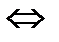 0.
0.
10. Любая сила уравновешенной системы сил является уравновешивающей по отношению к остальным силам этой системы.
11.Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил (обычно обозначаемой R).
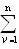 12.Главным вектором системы сил называют геометрическую сумму всех сил системы R = F v .
12.Главным вектором системы сил называют геометрическую сумму всех сил системы R = F v .
2. Аксиомы статики
Обобщая опыт изучения физических законов природы, Галилей и Ньютон сформулировали основные законы механики, которые могут рассматриваться как аксиомы механики, так как имеют в своей основе экспериментальные факты.
Аксиома I . (Аксиома инерции)
Рис.13
Для сил F 1 и F 2 , изображенных на рис.13, их скалярные моменты относительно точки О соответственно равны:
mom0 F 1 = M0(F 1 ) = +F 1 · h1 ;
mom0 F 2 = M0(F 2 ) = -F 2 · h2.
Скалярный (алгебраический) момент силы относительно точки имеет размерность Н×м, что вытекает из определяющей формулы этой величины.
Скалярный (алгебраический) момент пары сил
Пара сил (рис.14) – система двух равных, параллельных, противоположно направленных сил, линии действия которых не совпадают.
Силы пары математически соотносятся так:
| F2 = -F1. | (7) |
Их модули равны:
| F2 = F1= F . | (8) |
Плоскость, в которой лежат силы, образующие пару, называется плоскостью действия пары.
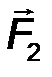
|
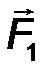
|
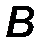
|
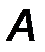
|
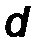
|
Рис.14
Кратчайшее расстояние между линиями действия сил пары называется плечом пары d (рис.14).
Рис.17
Проекцией силы F на плоскость 0xy называется вектор F xy , заключенный между проекциями начала и конца силы F на эту плоскость.
В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости 0xy (рис.17).
По модулю F xy = F·cos q, где q - угол между векторами F и F xy.
Проекция силы на плоскость используется, например, для нахождения проекций силы на оси, лежащие в этой плоскости (см. рис.17):
| F x = F xy · cos j = F·cos q cos j ; F y = F xy · sin j = F·cos q · sin j ; Fz= F·sinq. | (11) |
Здесь же написана формула и для проекции силы на ось 0z.
Момент силы относительно точки (векторный)
Определим радиус - вектор r как вектор, соединяющий начало координат (т. О) и некую точку в пространстве, например, точку приложения силы F (т.А).
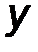
|
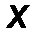
|
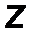
|
|
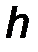
|

|

|
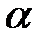
|
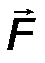
|
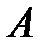
|

|
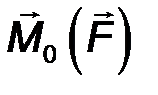
|
|
Рис.18
Момент силы F , вычисленный относительно точки есть векторное произведение радиус – вектора точки приложения силы на силу.
mom 0 F = [ r ∙ F ] = r × F. (12)
Модуль (величина) момента силы, вычисленного относительно точки определяется выражением:
| mom0 F = [r ∙ F] = r × F = 2S∆OAB . | (13) |
или равен произведению модуля силы F на её плечо h, равное кратчайшему расстоянию от точки 0 до линии действия силы F. Здесь:
· h = ОС - плечо силы - длина перпендикуляра, опущенного из точки 0 на линию действия силы F ;
· α- угол между векторами r и F.
Вектор mom 0 F направлен в соответствии с правилом векторного произведения.
Вектор mom0 F считается приложенным к точке 0 и перпендикулярен плоскости треугольника ОАВ, в которой лежат векторы r и F. При этом он направлен в сторону, с которой кратчайший поворот (на угол, меньший 180°) вектора r к вектору F (если его мысленно приложить к точке 0; см. рис.18) виден происходящим против хода часовой стрелки.
Модуль момента силы относительно точки измеряется в системе единиц СИ в ньютон - метрах (Н·м).
Свойства момента силы относительно точки
1. Момент силы относительно точки не изменится, если силу переносить вдоль линии ее действия.
2. Момент силы относительно точки не изменится, если точку переносить вдоль линии, параллельной линии действия силы.
3. Момент силы относительно точки равен нулю, если линия действия силы проходит через точку.
4. mom0 F = - mom0 (- F), при условии, что силы F и - F направлены по одной прямой.

Момент силы относительно оси
Моментом силы, вычисленным, относительно оси, называется проекция на эту ось момента силы, вычисленного относительно точки, лежащей на этой оси (рис.19).
mom e F = Пр e mom0 F .
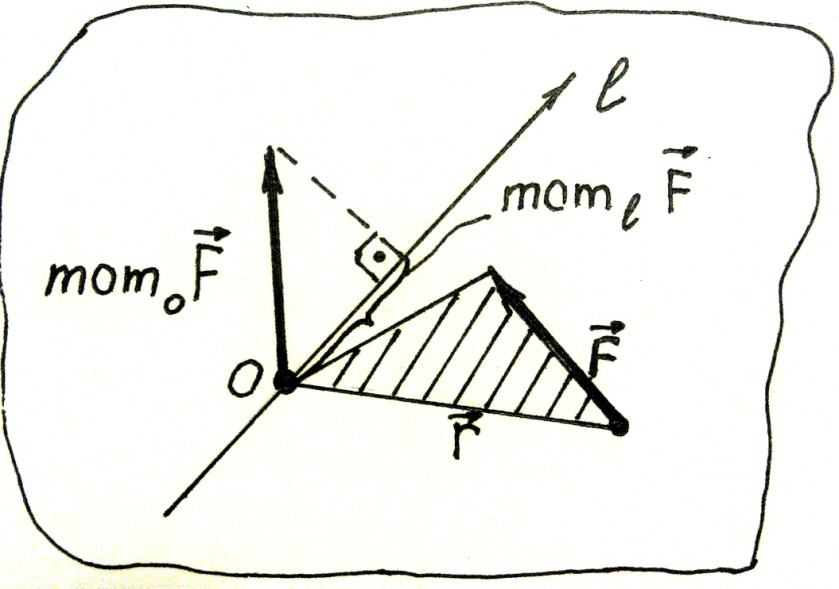
Рис.19
Теорема о вычислении момента силы относительно оси
Чтобы вычислить момент силы относительно оси, надо спроецировать эту силу на плоскость, перпендикулярную оси, найти модуль момента прекции силы относительно точки пересечения оси с плоскостью и приписать знак «+», если сила стремится повернуть тело вокруг данной оси против часовой стрелки и «-», если – по ходу часовой стрелки.
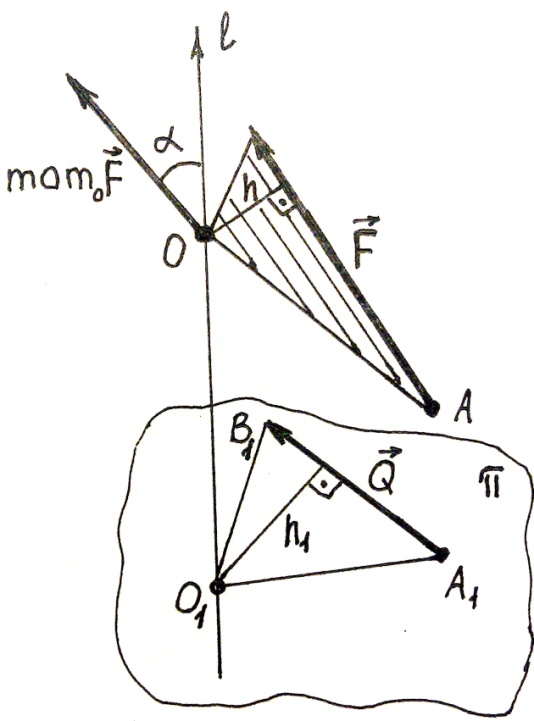
Рис.20
Пусть в точке А тела приложена сила F. Вектор mom 0 F направлен перпендикулярно плоскости треугольника ОАВ.
Проведем плоскость π перпендикулярно оси е , проходящей через точку О (рис.20). Q есть проекция силы F на плоскость π. Треугольник O1A1B1 есть проекция на эту плоскость треугольника ОАВ. Выразим зависимость между площадями этих треугольников.
S∆ O1A1B1 = S∆ABC ∙ |cos α| ,
где α угол между плоскостями треугольников. S∆A1B1C1 = ½ Qh1
Доказать, что mom e F = 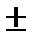 Qh 1 .
Qh 1 .
Доказательство:
mom e F = П p e mom 0 F = | mom 0 F | cos α = 2 S ∆ ABC cos α = 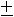 2 S ∆A1B1C1 =
2 S ∆A1B1C1 = 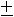 Qh 1 .
Qh 1 .
Следовательно, mom e F = 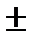 Qh . Теорема доказана.
Qh . Теорема доказана.
Свойства момента силы относительно оси
1. Момент силы, вычисленный относительно оси не зависит от выбора точки на оси.
2. Если линия действия силы параллельна оси или пересекает ось, то момент силы относительно оси равен нулю.
Момент силы относительно оси может определяться геометрически (рис.21).
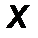
|
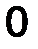
|
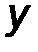
|
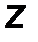
|
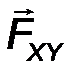
|
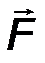
|
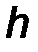
|
Рис.21
Например, для оси 0z:
| mom z F = ± FXY×h. | (14) |
Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси, стремится вращать тело против хода часовой стрелки, глядя с положительного направления оси.
Например, момент силы F на рис.21 относительно оси 0z равен произведению модуля её проекции |F xy| на плоскость 0xy на плечо h этой проекции относительно точки 0, взятое со знаком плюс: mom z F = + Fxy×h.
Моменты сил относительно координатных осей
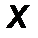
|
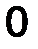
|
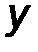
|
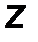
|
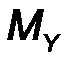
|
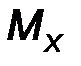
|
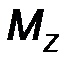
|
|
Рис.22
Момент силы относительно точки можно описать с помощью аппарата векторной алгебры, в соответствии с которым силу F необходимо задать своими проекциями Fx, Fy, Fz на оси координат и указать координаты x,y,z точки приложения этой силы (т.А). Векторный момент силы относительно начала координат 0 определяется аналитически следующим образом:
| mom 0 F = M 0 (F) = M x ∙ i + M y ∙ j + M z ∙k , (15) |
где i, j, k - орты координатных осей 0x, 0y, 0z, а проекции момента M 0 (F) (рис.22) вычисляются по следующим формулам:
| Mx = y Fz – z Fy, My = z Fx - x Fz, M z = x F y - y F x. | (16) |
Замечание: Проекции MX, MY, MZ по определению – это моменты сил относительно координатных осей 0x, 0y, 0z.
Модуль момента силы, вычисленного относительно точки определяется по формуле:
| |mom 0 F| = M 0 = √M2 x + M2 y + M2 z . | (17) |
Момент пары сил (векторный)
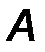
|
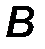
|
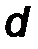
|
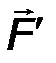
|
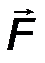
|
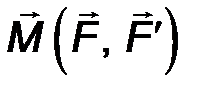
|
Рис.23
Момент пары сил (обозначается) M(F,F’) ≡ M ( F, F΄)≡ M П - определяется как момент (векторный) одной силы пары относительно точки приложения другой:
| M П = [BA ∙ F] ≡[AB ∙ F']. | (18) |
В соответствии с определением операции векторного произведения вектор момента пары ориентирован перпендикулярно плоскости действия пары. Учитывая, что F΄ = F, и используя правило векторного произведения, легко увидеть (рис.23), что оба приведенные в определяющей формуле векторных произведения приводят к одному и тому же результату. Момент пары сил направлен ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки. Его модуль
| M П = F·d , | (19) |
равен по величине площади параллелограмма, построенного на векторах пары. Здесь d- плечо пары.
Пара сил полностью характеризуется своим моментом.
Так же, как и в плоской статике, в пространственной статике действует теорема о сумме моментов сил пары.
Теорема о сумме моментов сил пары
Связи и реакции связей
В отличие от свободных тел, в природе чаще встречаются несвободныеточки и тела, перемещения которых в некоторых направлениях пространства ограничены другими объектами. Тела, ограничивающие свободу перемещения данной точки или тела, называются связями, наложенным на данную точку или тело. Несвободные материальные тела, нагруженные силами, действуют на связи силами, стремящимися эти связи преодолеть. Эти силы иногда называют - силы давления на связь. В соответствии с аксиомой статики о равенстве действия и противодействия, связи противодействуют возможному перемещению тела. Силы, с которыми связи действуют на рассматриваемый объект, называются силами реакций связей или реакциями связей, которые приложены к объекту в точке его соприкосновения со связью. Направление реакции связи противоположно тому, куда связь не дает перемещаться объекту.
Сформулируем еще раз основные определения, касающиеся связей.
Связи – всë, что ограничивает перемещение данного тела в пространстве.
Реакция связи – сила, с которой данная связь действует на тело.
Принцип освобождаемости от связей
Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями.
Основные виды связей:
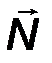
|
Рис.24
1. Гладкая опора. Это простой контакт тела с поверхностью, трением о которую можно пренебречь. Такая связь (рис.24) препятствует перемещению объекта только вдоль нормали к поверхности. Поэтому, реакция N такой связи перпендикулярна поверхности и носит название “нормальная реакция опоры”.
2. Невесомая нерастяжимая нить (трос, канат, цепь), (рис.25). Эта связь не дает перемещаться телу вдоль нити. Её реакция T приложена к телу, направлена вдоль нити к точке подвеса 0 и носит название “сила натяжения нити”.
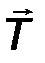
|
|
Рис.25
3. Цилиндрический шарнир, или подшипник (рис.26).
| 2 |
| 1 |
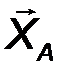
|
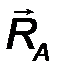
|
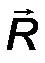
|
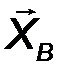
|
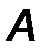
|
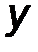
|
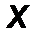
|
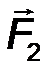
|
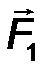
|
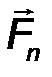
|
Рис.26
Цилиндрический шарнир - это устройство, запрещающее перемещение точек тела, принадлежащих оси шарнира и позволяющее осуществлять относительное вращение соединенных с его помощью тел в плоскости, перпендикулярной оси шарнира. Реакция R шарнира направлена в этой плоскости, т.е. перпендикулярна оси шарнира и имеет две ортогональные составляющие XA, YA. Математически её можно оценить по формуле:
| R A = √X 2 A + Y 2 A . | (21) |
4. Сферический шарнир (Рис.27). Такая связь допускает вращение тела в любом направлении в пространстве, но запрещает перемещение точки закрепления тела. Реакция RA может быть направлена в любую сторону и имеет три ортогональные составляющие XA, YA, ZA. Величина силы оценивается аналогично:
| RA = √X 2 A + Y 2 A + Z 2 A . | (22) |
|
|
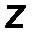
|
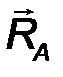
|
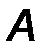
|
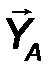
|
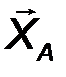
|
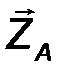
|
Рис.27
5. Невесомый шарнирно опертый стержень (рис.28). На стержень действуют лишь две реакции в шарнирах, приложенные к его концам. В покоящейся, уравновешенной системе, в соответствии с аксиомой статики, эти силы равны, противоположны и направлены по одной прямой, т.е. линии, соединяющей концы стержня при любой его форме (прямолинейной, криволинейной, ломаной):
RD = -RB .
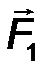
|

|
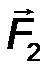
|
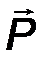
|
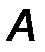
|
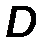
|
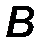
|
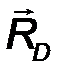
|
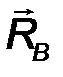
|
Рис.28
6. Жесткая заделка, или консоль. Это - балка с замурованным в стену концом, или гвоздь, вбитый в стену (рис.29). В заделке отсутствуют все перемещения линейные и угловые перемещения. Рассматривая плоской систему сил, в заделке возникает пара сил с моментом МА, препятствующая повороту балки и реакция RA с двумя ортогональными составляющим XA YA. Таким образом, в плоской консоли возникает два компонента реакции. Величина реакции определяется:
| RA = √X2A + Y2A . | (23) |
|
|
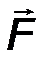
|
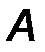
|
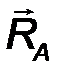
|
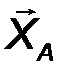
|
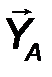
|
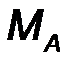
|
Рис.29
7. Подпятник (рис.30) – отличается от цилиндрического шарнира отсутствием возможности перемещения вдоль оси шарнира. Примером шарнира с подпятником может служить дверная или оконная петля. Такое ограничение приводит к появлению третьей составляющей реакции по оси 0Z.
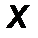
|
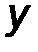
|
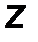
|
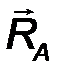
|
|
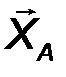
|
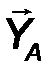
|
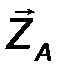
|
Рис.30
Реакция в подпятнике вычисляется по правилу геометрического сложения ортогональных векторных компонент:
| RA = √X 2 A + Y 2 A + Z 2 A . | (24) |
8. Подвижная шарнирная опора (рис.31).
Такая связь полностью идентична гладкой опоре. Линия действия реакции перпендикулярна опорной поверхности.
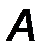
|
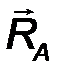
|
Рис.31
9. Тело опирается на неподвижную точку или гладкую линию (рис.32).
Реакция N A направлена по нормали к опирающейся поверхности.
10. Тело опирается точкой или гладкой линией (рис.32).
Реакции NВ и N с направлены по нормали к опорной поверхности.
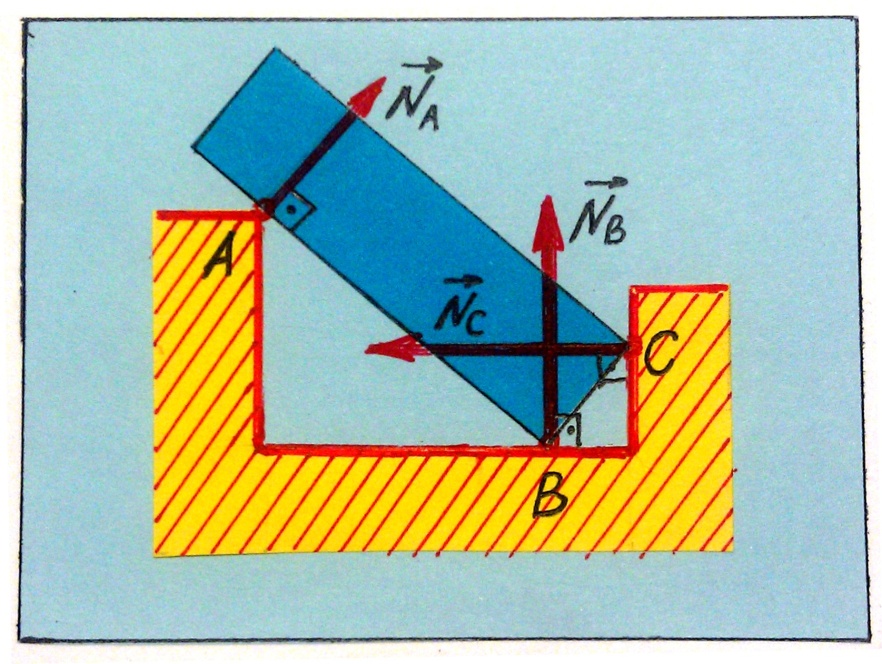
Рис.32
Произвольная пространственная система сил, действующих на абсолютно твердое тело, эквивалентна в общем случае силе, равной сумме всех сил системы и приложенной в произвольно выбранном центре приведения и паре сил, момент которой равен сумме моментов всех сил системы вычисленных относительно этого центра приведения.
Доказательство.
Пусть произвольная пространственная система сил:
F1 , F2 … Fn
A1, A2 … An .
приложена к абсолютно твердому телу (рис.35). Примем произвольную точку О за центр приведения. В точке О на основании второй и третьей аксиом статики добавим к данной системе сил уравновешенную систему сил подобную данной. Силы, приложенные в точке О, образуют систему сходящихся сил, которую в общем случае приводим к одной силе, равной их сумме. Оставшиеся силы образуют n пар сил, действия которых заменяем одной парой с моментом, равным сумме моментов этих пар.
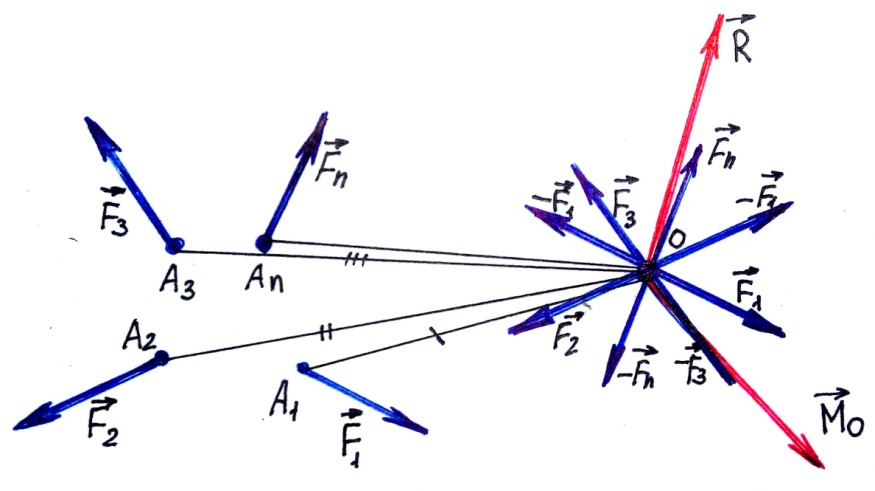
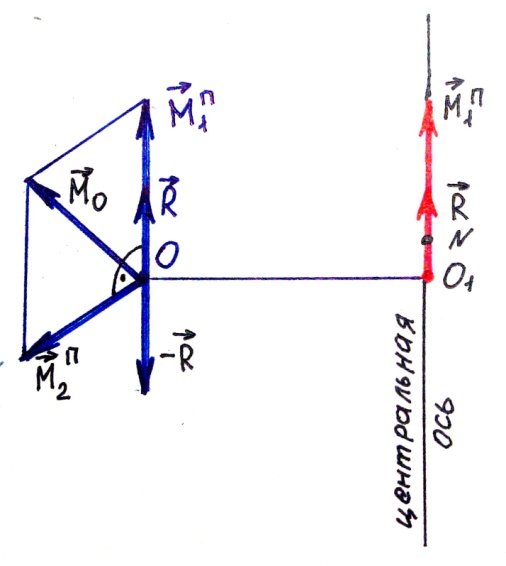
Рис.35 Рис.36
Запишем приведенное доказательство:
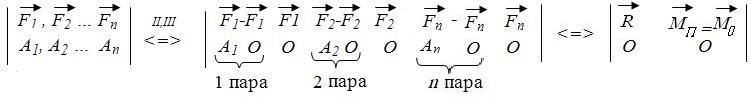
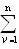
R = F 1 + F 2 + … F n = F v - главный вектор.
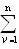
MП= mom0 F v = M 0 - главный момент.
5.3.Инварианты произвольной системы сил
Величины, которые остаются неизменными при каком-либо преобразовании, называются инвариантами по отношению к этому преобразованию.
Под инвариантами системы сил понимают величины, которые не изменяются при перемене центра приведения этой системы.
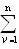 Первый инвариант – векторный инвариант - главный вектор произвольной системы сил не зависит от выбора центра приведения.
Первый инвариант – векторный инвариант - главный вектор произвольной системы сил не зависит от выбора центра приведения.
R = F v.
Второй инвариант – скалярный инвариант – скалярное произведение главного вектора на главный момент, вычисленный относительно произвольной точки не зависит от выбора центра приведения.
( R MN) = ( RMM) .
Примеры решения задач на равновесие
Пример на равновесие произвольной плоской системы сил
Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н·м; расстояние a = 1 м.(рис.56).
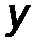
|
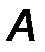
|
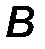
|
|

|
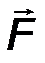
|

|
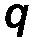
|

|
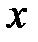
|
Рис.56
Дано: F = 60 Н, q = 15 Н/м, М = 40 Н·м, a = 1 м.
Определить: реакции неподвижного цилиндрического шарнира А и подвижного цилиндрического шарнира В.
Решение
1. Для определения опорных реакций рассмотрим равновесие балки АВ.
2. К балке АВ приложены активные силы: F, пара сил с моментом М и равномерно распределенная нагрузка интенсивностью q. Заменим распределенную нагрузку эквивалентной сосредоточенной Q, равной по модулю Q = q·2a = 30 Н и приложенной в средней точке нагруженного участка.
Введем декартову систему координат Аxy, совместив начало координат с неподвижным шарниром А и направив ось Аx вдоль балки.
На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями. Реакция R A неизвестна по величине и направлению, поэтому разложим её на две неизвестные по величине составляющие XA, YA, направленные по координатным осям. Опора в точке В не препятствует её перемещению вдоль наклонной плоскости и, следовательно, реакцию 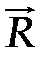 B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине (рис.57).
B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине (рис.57).
3.Имеем произвольную плоскую систему сил.
4. В задаче имеется три неизвестных скалярных величины: XA, YA, RB. Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой[4].
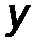
|
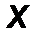
|
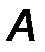
|
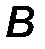
|
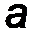
|
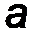
|
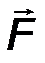
|

|
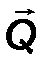
|

|
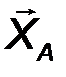
|
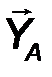
|

|
|
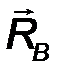
|
Рис.57
Составим уравнения равновесия для полученной эквивалентной силовой схемы.
Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:
∑ X = 0, X a – R b sin 30° = 0; (1)
∑ Y = 0, Y a – Q + F + R b cos 30° = 0; (2)
∑momA F = 0, -Q∙ a + F ∙2a + M + (R b cos 30°) ∙ 3a = 0. (3)
Напомним, что скалярные моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции R b относительно точки А выделена её вертикальная составляющая, равная R b cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.
Из третьего уравнения (2) и (3) находим:
RB = (Q - 2F - M/a)/(3cos 30°)  -50.0 Н .
-50.0 Н .
Подставив в первое и второе, получим:
Х A =((Q - 2F - M/a)/(3cos 30°))sin30° 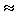 -25.0 Н ,
-25.0 Н ,
YA = (2 Q - F + M / a )/3 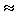 13,3 Н.
13,3 Н.
Полученные отрицательные значения RB и XA означают, что сила R b и составляющая реакции XA противоположны показанным на рис.57 направлениям этих векторов.
Величина реакции RA = (XA2 + YA2) 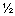
 28.3 Н.
28.3 Н.
Пример на равновесие произвольной пространственной системы сил
Горизонтальная прямоугольная плита весом Р (рис.58) закреплена с помощью сферического в точке А, цилиндрического шарнира в точке В и
невесомого шарнирно опертого стержня ДД  . На плиту в плоскости параллельной плоскости xz, действует сила F, а в плоскости, параллельной yz, - пара сил с моментом М.
. На плиту в плоскости параллельной плоскости xz, действует сила F, а в плоскости, параллельной yz, - пара сил с моментом М.
Дано: Р = 3 кН, F = 8 кН, М = 4 кН ∙ м,
ά = 60° , АС = 0,8 м, АВ = 1,2 м,
ВЕ = 0,4 м, ЕН = 0,4 м.
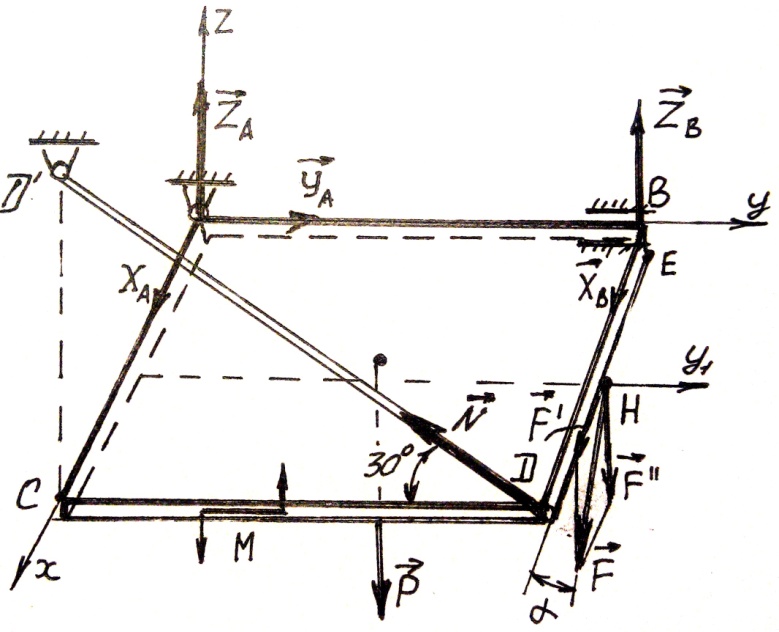
Определить: реакции опор А, В и стержня ДД  .
.
Рис.58
Решение.
1. Рассмотрим равновесие плиты АВДС.
2. На плиту действуют активные силы: Р, F и пара сил с моментом М, а также реакции связей. Реакцию неподвижного сферического шарнира разложим на три составляющие X  , Y
, Y 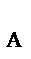 , Z
, Z 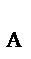 , неподвижного цилиндрического шарнира – на две составляющие X
, неподвижного цилиндрического шарнира – на две составляющие X 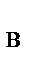 , Z
, Z 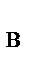 (в плоскости, перпендикулярной оси шарнира); реакцию N стержня направляем вдоль стержня от Д к Д
(в плоскости, перпендикулярной оси шарнира); реакцию N стержня направляем вдоль стержня от Д к Д 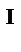 , предполагая, что он растянут.
, предполагая, что он растянут.
3. Имеем произвольную пространственную систему сил.
4. Составим уравнения равновесия для полученной эквивалентной силовой схемы.
Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:
∑ X = 0, X 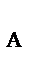 + X
+ X 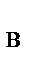 + F cos 60° = 0;
+ F cos 60° = 0;
∑ Y = 0, Y 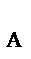 − N cos 30° = 0;
− N cos 30° = 0;
∑ Z = 0. Z 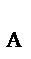 + Z
+ Z 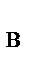 − Р + N sin 30° − F sin 60° = 0;
− Р + N sin 30° − F sin 60° = 0;
∑ mom 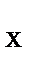 F = 0, М − Р ∙АВ/2 + Z
F = 0, М − Р ∙АВ/2 + Z 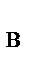 ∙ АВ − F sin 60° ∙ АВ + N sin 30° ∙ АВ = 0;
∙ АВ − F sin 60° ∙ АВ + N sin 30° ∙ АВ = 0;
∑ mom 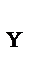 F = 0, Р ∙АС/2 + F sin 60° ∙ЕН − N sin 30° ∑АС − F cos 60° ∙ВЕ = 0;
F = 0, Р ∙АС/2 + F sin 60° ∙ЕН − N sin 30° ∑АС − F cos 60° ∙ВЕ = 0;
∑ mom 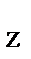 F = 0, −X
F = 0, −X 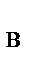 ∙АВ − N cos 30° ∙АС − F cos 60° ∙АВ = 0.
∙АВ − N cos 30° ∙АС − F cos 60° ∙АВ = 0.
Подставив в составленные уравнения числовые значения всех заданных
величин и решив эти уравнения, найдем искомые реакции: X 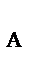 = 3,42 кН; Y
= 3,42 кН; Y 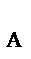 = 5,13 кН; Z
= 5,13 кН; Z 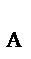 = 4,83 кН; X
= 4,83 кН; X 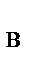 = −7,42 кН; Z
= −7,42 кН; Z 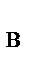 = 2,13 кН; N = 5,93кН. Знак «−» указывает на то, что реакция X
= 2,13 кН; N = 5,93кН. Знак «−» указывает на то, что реакция X 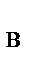 направлена противоположно показанной на рис.58.
направлена противоположно показанной на рис.58.
Список использованной литературы
1.Ишлинский А.Ю.Задачи механики. Препринт №185.М.:Ист-т пробл. Механики АН СССР, 1981.-38 с.
2.Конспект лекций по теоретической механике: Учебное пособие /В.А.Аршинова, А.И.Зайцев – Яросл. гос. ун-т. – Ярославль, 1998.- 176 с.:ил.- (Высшее образование).
3.Теоретическая механика: учебник /Н.Г.Васько, В.А.Волосухин, А.Н.Кабельков, А.Н.Бурцева – Ростов н/Д: Феникс,2012. – 302 с.:ил.- (Высшее образование).
4.Леготин С.Д. Основы теоретической механики: электронный учебник /М. Гос. Индустриальный ун-т, 2008.-136 с.:ил.-(Высшее образование).
За помощь при создании данного пособия выражается благодарность студентам машиностроительного факультета Аджояну М.Р и Выборнову Н.С.
[1] Единицей измерения силы в системе единиц СИ является Ньютон (Н); применяется и более крупная единица 1 кН=1000Н.
[2] Ортом вектора называется единичный вектор, направленный в ту же сторону и приложенный в той же точке, что и заданный вектор.
[3] Это следствие, также как и часть аксиом и теорем статики, применимо только для абсолютно твердого, не деформируемого тела.
[4] статически определимой задача статики называется, если число неизвестных компонентов реакций равно числу уравнений равновесия, и наоборот, задача статики называется статически неопределимой, если число неизвестных компонентов реакций больше числа уравнений равновесия.
СТАТИКА
Электронный учебник по дисциплине: ”Теоретическая механика”
для студентов заочной формы обучения
Соответствует Федеральному образовательному стандарту
(третьего поколения)
Сидоров В.Н.,д.т.н.,профессор
Ярославский государственный технический университет
Ярославль, 2014
СОДЕРЖАНИЕ
Введение …………………………………………………………………... 4
1.Основные понятия и определения статики ………………………........ 5
2.Аксиомы статики ……………………………………………………….. 9
3.Основные операции с силами в статике …………………..................... 14
3.1. Операции с силами в плоской (двухмерной) статике ………........ 15
Проекция силы на ось ………………………………………………15
Скалярный момент силы относительно точки ……………………16
Скалярный момент пары сил ………………………………………17
3.2. Операции с силами в пространственной (трехмерной) статике …20
Проекция силы на плоскость ……………………………………...20
Момент силы относительно точки ………………………………..22
Момент силы относительно оси …………………………………..23
Моменты силы относительно координатных осей ………………23
Момент пары сил …………………………………………………..24
4. Связи и реакции связей ………………………………………………...27
5. Произвольная пространственная система сил ………………………..33
5.1. Главный вектор и главный момент
произвольной пространственной системы сил …………………..33
5.2. Теорема о приведении произвольной
пространственной системы сил ………………………………..35
5.3. Инварианты произвольной пространственной
системы сил …………………………………………………….36
5.4. Частные случаи приведения произвольной
пространственной системы сил ……………………………….37
5.5. Алгоритм решения задач на приведение произвольной
пространственной системы сил к простейшему виду ……….41
5.6. Условия равновесия произвольной пространственной
системы сил …………………………………………………….42
6. Вывод условий равновесия различных систем сил из условий
равновесия произвольной пространственной системы сил ………..43
6.1. Условия равновесия плоской системы сил ……………………...44
6.2. Условия равновесия системы параллельных сил ……………….45
6.3. Условия равновесия системы сходящихся сил ………………...45
7. Алгоритм решения задач по статике на равновесие систем сил ….47
8. Замена распределенных сил эквивалентными
сосредоточенными силами …………………………………………47
9. Теорема о зависимости между главными моментами системы
сил относительно двух точек …………………………………….…50
10. Теорема Вариньона для системы сходящихся сил ……………....50
11. Центр системы параллельных сил и центр тяжести …………..…50
11.1. Центр системы параллельных сил ………………………….....50
11.2. Определение положения центра тяжести тела …………….....52
11.3. Методы определения центра тяжести ………………………...54
12. Равновесие тел при наличии трения .................................................57
12.1. Равновесие твердого тела при наличии трения скольжения ...57
12.2. Равновесие твердого тела при наличии трения качения …....58
13. Примеры решения задач на равновесие……………………….…59
Введение
«Кто не знаком с законами механики
тот не может познать природы»
Галилео Галилей
Значение механики, ее значительная роль в совершенствовании производства, повышении его эффективности, ускорении научно-технического процесса и внедрении научных разработок, росте производительности труда и улучшении качества выпускаемой продукции, к сожалению, понимается достаточно отчетливо не всеми руководителями министерств и ведомств, высших учебных заведений, равно как и то, что представляет механика наших дней /1/. Как правило, о ней судят по содержанию теоретической механики, изучаемой во всех высших технических учебных заведениях.
Студенты должны знать, насколько важна теоретическая механика, как одна из основополагающих инженерных дисциплин высшей школы, научная основа важнейших разделов современной техники, своеобразный мост, соединяющий математику и физику с прикладными науками, с будущей профессией. На занятиях по теоретической механике впервые студентам прививается системное мышление, умение ставить и решать практические задачи. Решать их до конца, до числового результата. Учиться анализировать решение, устанавливать границы его применимости и требование к точности исходных данных.
Не менее важно знать студентам, что теоретическая механика лишь вводная, хотя и совершенно необходимая, часть колоссального здания современной механики в широком понимании этой фундаментальной науки. Что она будет развиваться в других разделах механики: сопротивлении материалов, теории пластин и оболочек, теории колебаний, регулирования и устойчивости, кинематике и динамики машин и механизмов, механике жидкости и газа, химической механике.
Достижения всех разделов машиностроения и приборостроения, строительной индустрии и гидротехники, добычи и переработки руды, каменного угля, нефти и газа, железнодорожного и автомобильного транспорта, судостроения, авиации и космической техники опираются на глубокое понимание законов механики.
При подготовке лекций автором использованы методические разработки кафедры теоретической механики Ярославского государственного технического университета /2/ и других известных университетов /3, 4/.
Учебное пособие предназначено для студентов машиностроительных, автомеханических специальностей заочной формы обучения в техническом университете по сокращенной программе курса.
Итак, несколько определений.
Теоретическая механика – это наука, изучающая общие законы механического движения и равновесия материальных объектов и возникающие при этом механические взаимодействия между материальными объектами.
Под механическим движением материального объекта понимают происходящее с течением времени изменение его положения по отношению к другим материальным объектам.
Под механическим взаимодействием подразумевают такие действия тел друг на друга, при которых изменяются движения этих тел, либо они сами деформируются (меняют свою форму).
Теоретическая механика состоит из трех разделов: статики, кинематики и динамики.
Статика – рассматривает два основных вопроса:
а) сложение сил и приведение системы сил к простейшему виду;
б) определение необходимых и достаточных условий равновесия, действующих на абсолютно твердое тело систем сил.
Кинематика - изучает различные движения материальных точек, абсолютно твердых тел и механических систем, но не рассматриваются причины, вызывающие изменение характера движения.
Динамика - рассматривает влияние сил на состояние движения материальных точек, абсолютно твердых тел и механических систем.
1. Основные понятия и определения статики
1.Материальное тело – некоторое количество вещества, заполняющее определенный объем.
2.Материальная точка – тело, имеющее конечную массу, но размерами которого можно пренебречь по сравнению с расстояниями до других тел.
3. Масса – мера инертности тела и его гравитационных свойств.
4.Абсолютно твердое тело – тело, расстояния между любыми точками которого не изменяются с течением времени..
Из последнего определения вытекает, что такое тело – не деформируемое (абсолютно жесткое). Сама же механика – классическая (не релятивистская) механика, т.е. механика, в которой тела движутся со скоростями, существенно меньшими скорости света.
5.Свободная материальная точка (или тело) – такая, на перемещение которой не наложено никаких ограничений. Если перемещение материальной точки (или тела) в пространстве ограничивается другими телами, то ее называют несвободной или связанной . Тела, ограничивающие движение тела, называют связями.
6.Изолированная материальная точка (или тело) – такая, на которую не действуют никакие другие тела.
7.Сила есть мера механического воздействия одного тела на другое. Она характеризует величину и направление этого взаимодействия.
Силу (от английского слова “Force”) принято обозначать большой латинской буквой F, либо другой буквой.
Сила - вектор, при обозначении которого необходимо указывать признаки векторной величины, т.е. указывать надстрочную стрелку, либо саму букву выделять жирным шрифтом F  F.
F.
Указанные здесь обозначения силы эквивалентны, поэтому они объединены символом тождественности «  », или эквивалентности «
», или эквивалентности « 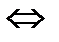 ».
».
Действие силы на тело определяется:
· модулем или абсолютным значением силы (обозначается | F|  F) – это величина силы, выраженная в неких единицах измерения[1];
F) – это величина силы, выраженная в неких единицах измерения[1];
· направлением силы (ортом[2] e);
· точкой приложения силы (т. A).
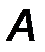
|
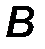
|

|
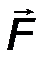
|
Рис.1
Прямая, вдоль которой направлена сила, называется линией действия силы (линия AB, рис.1).
Сила может быть задана:
- геометрическим способом, то есть как вектор с известным модулем F и известным направлением, определяемым ортом e;
- аналитическим способом, то есть её проекциями FX, FY, FZ на оси выбранной системы координат 0xyz .
Проекции силы определяются её модулем и углами α, β и γ, которые образует сила с координатными осями 0x, 0y, 0z, следующими соотношениями:
Fx = F cos α, Fy = cos β, F z = F z cos γ. (1)
Проекция силы на ось равна произведению модуля силы на косинус угла между этой силой и осью.
Модуль силы определяется через свои проекции (рис.2), как:
F = √ F 2 x + F2 y + F2 z . (2)

|
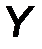
|
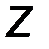
|
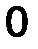
|
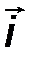
|
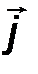
|
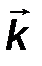
|
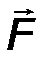
|
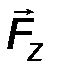
|
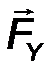
|
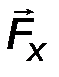
|
Рис.2
Материальные тела могут действовать друг на друга путем непосредственного соприкосновения или на расстоянии. В зависимости от этого силы можно разделить на поверхностные силы, приложенные к поверхности тела (например, силы давления на тело со стороны окружающей среды) и объемные силы, приложенные к данной части тела (например, силы тяготения).
Поверхностные и объемные силы называют распределенными силами. В ряде случаев силы можно рассматривать распределенными по некоторой кривой (например, т.н. «погонный вес», или вес одного метра длины тонкого стержня). Распределенные силы характеризуются их интенсивностью, то есть величиной силы, приходящейся на единицу длины, площади или объема. Интенсивность может быть постоянной (равномерно распределенные силы) или переменной величиной (см. раздел 8).
Если можно пренебречь малыми размерами области действия распределенных сил, то рассматривают сосредоточенную силу, приложенную к телу в одной точке (условное понятие, так как практически приложить силу к одной точке тела нельзя).
Таким образом, можно сформулировать следующую классификацию сил по степени их локализации:
· сосредоточенные силы;
· распределенные силы, в том числе:
- линейно распределенные;
- поверхностные;
- объемные.
По принадлежности к рассматриваемой механической системе силы можно разделить на внешние и внутренние.
Внешними называются силы, которые действуют на это тело (систему) со стороны других тел, внутренними - силы, с которыми части данного тела (данной системы) взаимодействуют друг с другом.
7.Системой сил называют совокупность сил F 1 , F 2 ,… Fn , приложенных к определенному телу (рис.3).
В зависимости от расположения линий действия сил систему сил называют:
· плоской, если линии действия всех сил лежат в одной плоскости;
· пространственной, если линии действия сил не лежат в одной плоскости;
· системой сходящихся сил, если линии действия всех сил пересекаются в одной точке;
· системой параллельных сил, если линии действия всех сил параллельны друг другу.
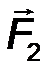
|
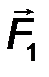
|
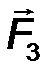
|
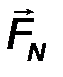
|

|
Рис.3
8. Две системы сил называются эквивалентными, если при замене одной системы сил, приложенных к свободному твердому телу, другой системой сил кинематическое состояние тела не изменится.
Замечание. Если каждая из двух систем сил порознь эквивалентны третьей, то эти две системы эквивалентны между собой.
S 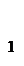
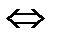 S
S 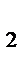 ; S
; S 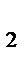
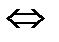 S
S  ;
; 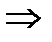 S
S 
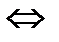 S
S  .
.
9. Система сил называется уравновешенной или эквивалентной нулю, если в результате её приложения кинематическое состояние абсолютно твердого тела не изменится S 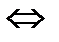 0.
0.
10. Любая сила уравновешенной системы сил является уравновешивающей по отношению к остальным силам этой системы.
11.Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил (обычно обозначаемой R).
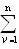 12.Главным вектором системы сил называют геометрическую сумму всех сил системы R = F v .
12.Главным вектором системы сил называют геометрическую сумму всех сил системы R = F v .
2. Аксиомы статики
Обобщая опыт изучения физических законов природы, Галилей и Ньютон сформулировали основные законы механики, которые могут рассматриваться как аксиомы механики, так как имеют в своей основе экспериментальные факты.
Аксиома I . (Аксиома инерции)
Дата: 2018-11-18, просмотров: 823.