Аксиома II. ( О равновесии двух сил)
Для равновесия двух сил, приложенных к абсолютно твёрдому телу необходимо и достаточно, чтобы эти силы были равны по величине и действовали по одной прямой в противоположные стороны (рис.4).
|
|
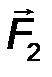
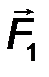
Рис.4
Математически такие силы связаны друг с другом соотношением инверсии:
| F2 = -F1. | (1.5) |
Аксиома III. (О присоединении и отбрасывании)
Действие данной системы сил на абсолютно твёрдое тело не изменится, если к этой системе сил добавить (или удалить) уравновешенную систему сил. Это означает, что вновь полученная система сил эквивалентна исходной.
1 следствие. Действие силы на абсолютно твёрдое тело не изменится если эту силу перенести вдоль линии действия силы в любую другую точку (т.е. сила является скользящим вектором[3]).
|
|
|
|
|
|
|
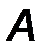
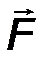
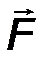
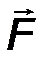
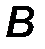
Рис.5
Дано: 
. Доказать, что 
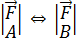точки А и В 
одной прямой.
Доказательство. Пусть на тело действует сила F, приложенная в точке А (рис.5). Приложим в точке В, принадлежащей линии действия силы, уравновешенную систему из двух одинаковых и противоположно направленных сил, также ориентированных вдоль линии АВ и равных по модулю F. Рассматривая две крайние силы из полученной системы трех сил, легко увидеть, что они также образуют уравновешенную систему. Отбросим её, тогда в системе останется только одна сила, приложенная в точке В, равная исходной, что и требовалось доказать.
2 следствие. Любая сила уравновешенной системы сил взятая в противоположном направлении, является равнодействующей для остальных.
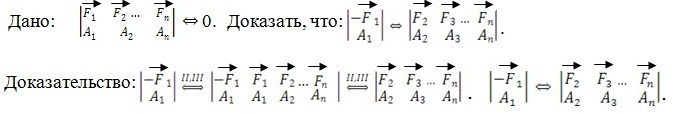
В этой записи над знаком эквивалентности (<=>) двух систем сил, стоят номера аксиом, использованных при переходе от одной системы сил к другой.
Аксиома IV . (О равнодействующей двух сил)
Равнодействующая двух неуравновешенных сил, приложенных к абсолютно твердому телу в одной точке всегда существует и определяется по правилу сложения векторов (рис.6).
|
|
|
|
|
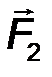
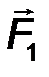
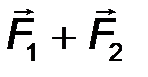
Рис.6
Следствие 1 . Силы, приложенные к одной точке твёрдого тела, складываются по правилу параллелограмма: их равнодействующая R соответствует диагонали параллелограмма, построенного на этих силах, как на сторонах (рис.7).
|
|
|
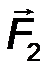
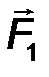
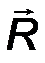
Рис.7
Следствие 2. Сложение сил можно осуществлять по правилу треугольника: их равнодействующая R соответствует вектору, начало которого совпадет с началом вектора F 1 , а конец – с концом вектора F 2 при условии, что начало F 2 совмещено с концом вектора F 1 (рис.8).
|
|
|
|
|
|
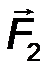
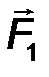
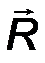
Рис.8
Такие сложения сил обозначаются векторной суммой:
| R = F1 + F2 . | (3) |
.
Модуль равнодействующей может быть вычислен с использованием теоремы косинусов по следующей формуле:
R = (F12 +F22 +2F1 F2 cos α)  ,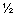
| (4) |
где α- угол между силами F1 и F2.
Обратная сложению сил является операция разложения сил.
Если на тело действует сила, то её действие можно заменить несколькими силами, называемыми составляющими.
Замена одной силы несколькими называется разложением силы на составляющие по заданным направлениям.
Для плоской, двухмерной статики чаще всего производят разложение силы на составляющие по двум взаимно перпендикулярным направлениям (рис.9). Для объёмной, трёхмерной статики – на три взаимно перпендикулярных направления (см. рис.2). Для этого силу проецируют на заданные оси.
|
|
|
|
|
|
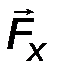
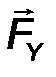
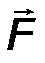
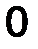
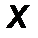
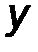
Рис.9
Следствие 3 ( Теорема о трех непараллельных силах).
Дата: 2018-11-18, просмотров: 505.
