Вращательный эффект пары сил характеризуется величиной, называемой моментом пары.
Скалярный (алгебраический) момент пары сил (обозначается М( F 1 , F 2 ) ≡
M ( F 1 , F 2 ) ≡ M П ) равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары:
| M П =± F·d. | (9) |
| 1 |
| 2 |
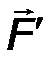
|
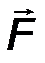
|
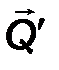
|
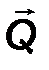
|
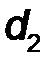
|
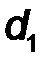
|
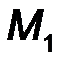 П П
|
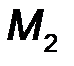 П П
|
Рис.15
Правило знаков моментов пар сил аналогично правилу для скалярных моментов сил относительно точки: момент считается положительным, если силы пары стремится повернуть тело против хода часовой стрелки, и отрицательным - по ходу часовой стрелки.
Для показанных на рис.15 пар сил (F , F ’ ) и (Q , Q ’) их моменты имеют противоположные знаки: M1 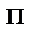 = + F ·d1; M
= + F ·d1; M 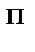 2= -Q·d2.
2= -Q·d2.
Поскольку действие пары сил на тело полностью характеризуется её моментом, на рисунках пару сил принято изображать дуговой стрелкой, показывающей направление действия момента (рис.15.2).
Теорема о сумме моментов сил пары
Сумма скалярных (алгебраических) моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости её действия, не зависит от выбора центра и равна моменту пары.
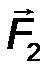
|
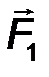
|
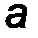
|
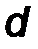
|
|
Рис.16
Докажем это (рис.16). Имеем пару сил (F 1 ; F 2), момент которой равен М 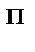 = F1× d = = F2× d. Найдём моменты силы F 1 и силы F 2 относительно точки О, а затем сумму моментов этих сил.
= F1× d = = F2× d. Найдём моменты силы F 1 и силы F 2 относительно точки О, а затем сумму моментов этих сил.
mom0 F1= -F1× а ;
mom0 F2= F2× (d+ a).
Так как F1 = F2, то:
mom0 F1+ mom0 F 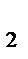 = - F1× а + F2× (d+ a)= F2× d = М
= - F1× а + F2× (d+ a)= F2× d = М 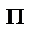 . (10)
. (10)
Полученная оценка не зависит от местонахождения центра (точки О). Таким образом, теорема доказана.
3.2. Операции с силами в пространственной (трехмерной) статике
Проекция силы на плоскость
|
|
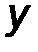
|
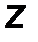
|
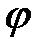
|
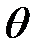
|
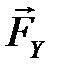
|
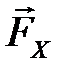
|
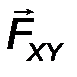
|
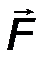
|
|
Рис.17
Проекцией силы F на плоскость 0xy называется вектор F xy , заключенный между проекциями начала и конца силы F на эту плоскость.
В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости 0xy (рис.17).
По модулю F xy = F·cos q, где q - угол между векторами F и F xy.
Проекция силы на плоскость используется, например, для нахождения проекций силы на оси, лежащие в этой плоскости (см. рис.17):
| F x = F xy · cos j = F·cos q cos j ; F y = F xy · sin j = F·cos q · sin j ; Fz= F·sinq. | (11) |
Здесь же написана формула и для проекции силы на ось 0z.
Момент силы относительно точки (векторный)
Определим радиус - вектор r как вектор, соединяющий начало координат (т. О) и некую точку в пространстве, например, точку приложения силы F (т.А).
|
|
|
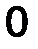
|
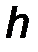
|

|

|
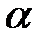
|
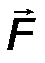
|
|

|
|
|
Рис.18
Момент силы F , вычисленный относительно точки есть векторное произведение радиус – вектора точки приложения силы на силу.
mom 0 F = [ r ∙ F ] = r × F. (12)
Модуль (величина) момента силы, вычисленного относительно точки определяется выражением:
| mom0 F = [r ∙ F] = r × F = 2S∆OAB . | (13) |
или равен произведению модуля силы F на её плечо h, равное кратчайшему расстоянию от точки 0 до линии действия силы F. Здесь:
· h = ОС - плечо силы - длина перпендикуляра, опущенного из точки 0 на линию действия силы F ;
· α- угол между векторами r и F.
Вектор mom 0 F направлен в соответствии с правилом векторного произведения.
Вектор mom0 F считается приложенным к точке 0 и перпендикулярен плоскости треугольника ОАВ, в которой лежат векторы r и F. При этом он направлен в сторону, с которой кратчайший поворот (на угол, меньший 180°) вектора r к вектору F (если его мысленно приложить к точке 0; см. рис.18) виден происходящим против хода часовой стрелки.
Модуль момента силы относительно точки измеряется в системе единиц СИ в ньютон - метрах (Н·м).
Свойства момента силы относительно точки
1. Момент силы относительно точки не изменится, если силу переносить вдоль линии ее действия.
2. Момент силы относительно точки не изменится, если точку переносить вдоль линии, параллельной линии действия силы.
3. Момент силы относительно точки равен нулю, если линия действия силы проходит через точку.
4. mom0 F = - mom0 (- F), при условии, что силы F и - F направлены по одной прямой.

Момент силы относительно оси
Моментом силы, вычисленным, относительно оси, называется проекция на эту ось момента силы, вычисленного относительно точки, лежащей на этой оси (рис.19).
mom e F = Пр e mom0 F .
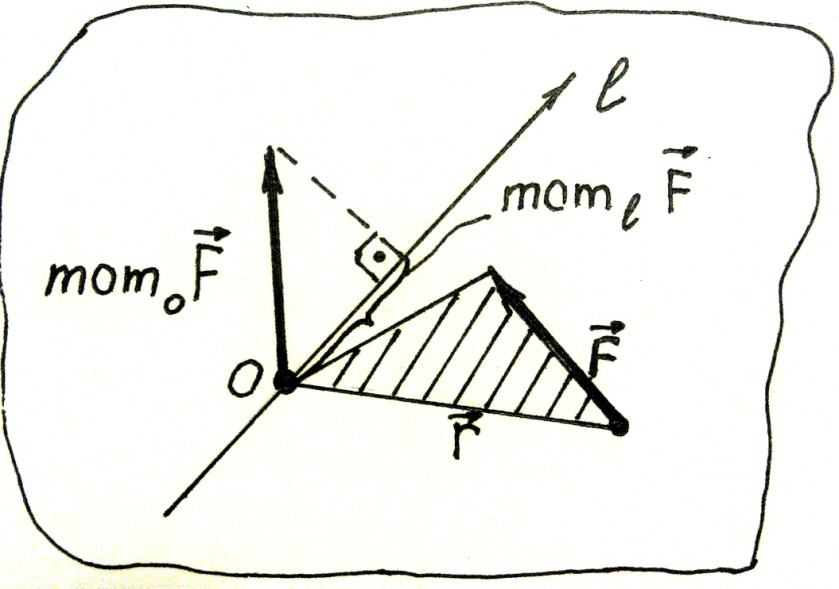
Рис.19
Теорема о вычислении момента силы относительно оси
Чтобы вычислить момент силы относительно оси, надо спроецировать эту силу на плоскость, перпендикулярную оси, найти модуль момента прекции силы относительно точки пересечения оси с плоскостью и приписать знак «+», если сила стремится повернуть тело вокруг данной оси против часовой стрелки и «-», если – по ходу часовой стрелки.
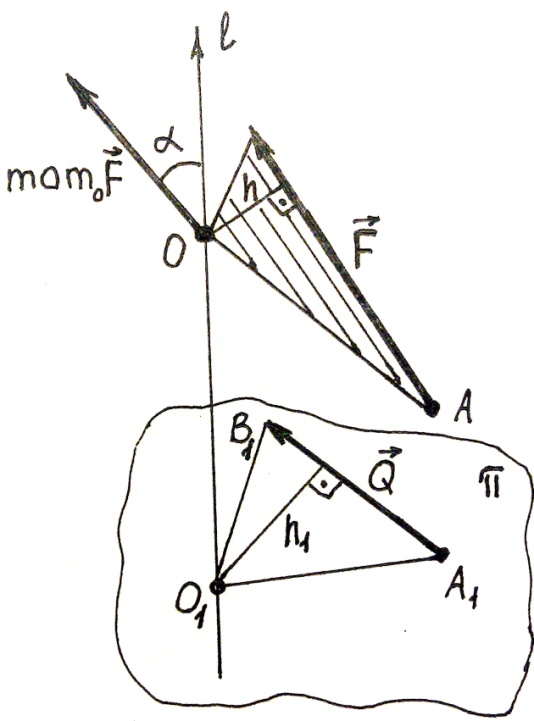
Рис.20
Пусть в точке А тела приложена сила F. Вектор mom 0 F направлен перпендикулярно плоскости треугольника ОАВ.
Проведем плоскость π перпендикулярно оси е , проходящей через точку О (рис.20). Q есть проекция силы F на плоскость π. Треугольник O1A1B1 есть проекция на эту плоскость треугольника ОАВ. Выразим зависимость между площадями этих треугольников.
S∆ O1A1B1 = S∆ABC ∙ |cos α| ,
где α угол между плоскостями треугольников. S∆A1B1C1 = ½ Qh1
Доказать, что mom e F = 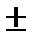 Qh 1 .
Qh 1 .
Доказательство:
mom e F = П p e mom 0 F = | mom 0 F | cos α = 2 S ∆ ABC cos α = 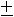 2 S ∆A1B1C1 =
2 S ∆A1B1C1 = 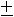 Qh 1 .
Qh 1 .
Следовательно, mom e F = 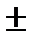 Qh . Теорема доказана.
Qh . Теорема доказана.
Свойства момента силы относительно оси
1. Момент силы, вычисленный относительно оси не зависит от выбора точки на оси.
2. Если линия действия силы параллельна оси или пересекает ось, то момент силы относительно оси равен нулю.
Момент силы относительно оси может определяться геометрически (рис.21).
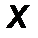
|
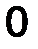
|
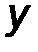
|
|
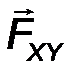
|
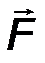
|
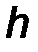
|
Рис.21
Например, для оси 0z:
| mom z F = ± FXY×h. | (14) |
Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси, стремится вращать тело против хода часовой стрелки, глядя с положительного направления оси.
Например, момент силы F на рис.21 относительно оси 0z равен произведению модуля её проекции |F xy| на плоскость 0xy на плечо h этой проекции относительно точки 0, взятое со знаком плюс: mom z F = + Fxy×h.
Моменты сил относительно координатных осей
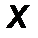
|
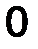
|
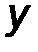
|
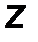
|
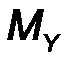
|
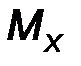
|
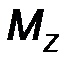
|
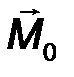
|
Рис.22
Момент силы относительно точки можно описать с помощью аппарата векторной алгебры, в соответствии с которым силу F необходимо задать своими проекциями Fx, Fy, Fz на оси координат и указать координаты x,y,z точки приложения этой силы (т.А). Векторный момент силы относительно начала координат 0 определяется аналитически следующим образом:
| mom 0 F = M 0 (F) = M x ∙ i + M y ∙ j + M z ∙k , (15) |
где i, j, k - орты координатных осей 0x, 0y, 0z, а проекции момента M 0 (F) (рис.22) вычисляются по следующим формулам:
| Mx = y Fz – z Fy, My = z Fx - x Fz, M z = x F y - y F x. | (16) |
Замечание: Проекции MX, MY, MZ по определению – это моменты сил относительно координатных осей 0x, 0y, 0z.
Модуль момента силы, вычисленного относительно точки определяется по формуле:
| |mom 0 F| = M 0 = √M2 x + M2 y + M2 z . | (17) |
Момент пары сил (векторный)
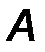
|
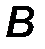
|
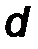
|
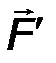
|
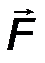
|
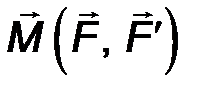
|
Рис.23
Момент пары сил (обозначается) M(F,F’) ≡ M ( F, F΄)≡ M П - определяется как момент (векторный) одной силы пары относительно точки приложения другой:
| M П = [BA ∙ F] ≡[AB ∙ F']. | (18) |
В соответствии с определением операции векторного произведения вектор момента пары ориентирован перпендикулярно плоскости действия пары. Учитывая, что F΄ = F, и используя правило векторного произведения, легко увидеть (рис.23), что оба приведенные в определяющей формуле векторных произведения приводят к одному и тому же результату. Момент пары сил направлен ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки. Его модуль
| M П = F·d , | (19) |
равен по величине площади параллелограмма, построенного на векторах пары. Здесь d- плечо пары.
Пара сил полностью характеризуется своим моментом.
Так же, как и в плоской статике, в пространственной статике действует теорема о сумме моментов сил пары.
Теорема о сумме моментов сил пары
Дата: 2018-11-18, просмотров: 806.