Из общих условий равновесия для произвольной пространственной системы сил получаются условия равновесия для частных систем сил, приложенных к твердому телу.

Из общих условий равновесия тел произвольной пространственной системы сил получается условие равновесия частных систем сил, приложенных к твёрдому телу.

6.1. Условия равновесия плоской  системы сил

Плоской называется такая система сил, линии действия которой расположены в одной плоскости.

· Векторная форма условий равновесия

Для равновесия (произвольной) плоской системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент системы сил, вычисленные относительно произвольно выбранной точки были равны нулю.

                         R = 0, M ₀ = 0.

· Координатная (аналитическая) форма условий равновесия

Для равновесия (произвольной) плоской системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил системы сил на каждую из двух координатных осей были равны нулю и сумма скалярных моментов всех сил, вычисленная относительно произвольной точки была равна нулю.

∑ X = 0; ∑ Y = 0; ∑ mom ₀ F = 0.

Другие формы условий равновесия плоской системы сил

1. 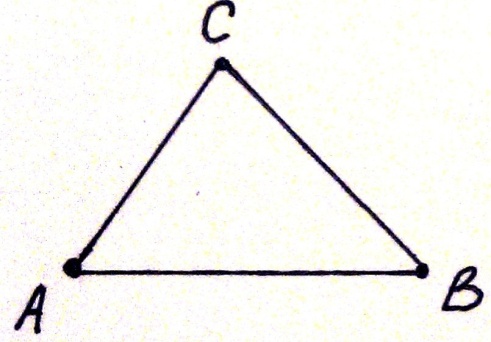Для равновесия плоской системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы скалярных моментов всех сил, вычисленных относительно каждой из трех  точек, не лежащих на одной прямой,  были  равны нулю.

∑ mom _A F = 0;

∑ mom _B F = 0;

∑ mom _C F = 0.                                                                    Рис. 40

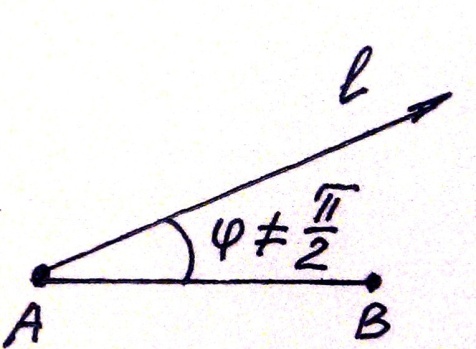
2. . Для равновесия плоской системы сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы скалярных моментов всех сил, вычисленных относительно каждой из двух произвольно выбранных точек, были равны нулю и сумма проекций всех сил на ось, не перпендикулярную отрезку, соединяющему эти две точки, была равна нулю.

∑ mom _A F = 0;

∑ mom _B F = 0;                                                                                 Рис .41

∑ Пр _{е AB} F = 0.

      6.2. Условия равновесия  системы параллельны сил

Если линии действия всех сил системы параллельны, то она называется системой параллельных сил.

· Векторная форма условий равновесия

Для равновесия системы параллельных сил, приложенных  к свободному абсолютно твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент системы сил, вычисленные относительно произвольно выбранной точки были равны нулю.

                         R = 0, M ₀ = 0.

· Координатная (аналитическая) форма условий равновесия

Для равновесия пространственной системы параллельных сил, приложенных к свободному абсолютно твердому телу, необходимо и достаточно, чтобы сумма проекций всех сил системы сил на ось, параллельную силам, была равна нулю и суммы моментов всех сил, вычисленные относительно каждой из двух других координатных осей были равны нулю.

∑ Z = 0;

∑ mom _x F = 0;

∑ mom _y F = 0.

Для равновесия плоской системы параллельных сил, приложенных к свободному абсолютно твердому телу, необходимо и достаточно, чтобы сумма проекций всех сил системы сил на ось, параллельную силам, была равна нулю и сумма, скалярных моментов всех сил, вычисленных относительно произвольной точки была равна нулю.

∑ Z = 0;

∑ mom ₀ F = 0.

        6.3. Условие равновесия  системы сходящихся сил

Системой сходящихся сил называется такая система сил, линии действия которых пересекаются в одной точке, называемой точкой схода.

· Векторная форма условий равновесия

Для равновесия  системы сходящихся сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен  нулю.

R = 0.

· Координатная (аналитическая) форма условий равновесия

Для равновесия пространственной  системы сходящихся сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из трех координатных осей были равны нулю.

∑ X = 0; ∑ Y = 0; ∑ Z = 0.

Для равновесия плоской  системы сходящихся сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из двух координатных осей были равны нулю.

∑ X = 0; ∑ Y = 0 .

· Геометрическая форма условий равновесия

Для равновесия системы сходящихся сил, приложенной к свободному абсолютно твердому телу, необходимо и достаточно, чтобы силовой многоугольник был замкнут.

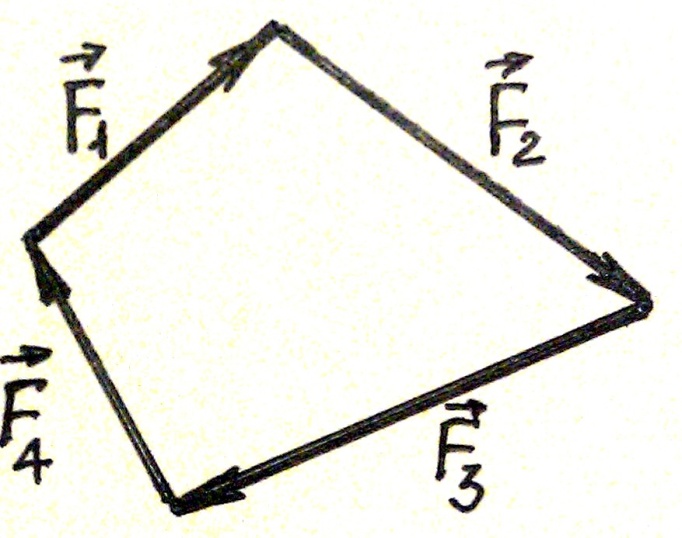
Рис.42