| M 0 (F) + M 0 (F΄) = M П . | (20) |
Докажем эту теорему.
Формально выбрав в пространстве некую точку (центр 0), подсчитаем сумму моментов сил пары, изображенной, например, на рис. 23 (точка 0 не показана). Учтем при этом, что F΄ = - F и OA = OB + BA,
тогда:
M 0 ( F ) + M 0 ( F΄ ) = [ OA ∙ F ]+[ OB ∙ F΄ ]=[ OA ∙ F ]+[ OB ∙ (- F )] = [ OA ∙ F ]-[ OB ∙ F ]=
[( OA – OB ) ∙ F ]=[ BA ∙ F ]=[ BA ∙ F ]= M ( F , F΄ )= M П .
что и требовалось доказать.
Следствие
Пары сил могут быть перемещены в любое место абсолютно твердого тела, при этом оказываемый ими вращательный эффект на тело не изменится.
Это следствие вытекает из независимости полученной оценки от выбора центра, а это означает и справедливость обратного утверждения, т.е. независимость результата от местонахождения самой пары.
Другая формулировка этого же следствия:
Момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором.
Приведем без доказательств еще несколько утверждений и теорем эквивалентности пар:
· Пару сил можно переносить в любую плоскость, параллельную плоскости пары.
· Пару сил можно переносить в ее плоскости в любое другое место.
· Силы пары можно изменять обратно пропорционально плечам пары.
· Пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие.
· Силы пары можно синхронно поворачивать, одновременно меняя их величину так, чтобы момент оставался неизменным.
· Пары сил можно складывать, при этом моменты пар сил складываются по правилу сложения векторов.
Связи и реакции связей
В отличие от свободных тел, в природе чаще встречаются несвободныеточки и тела, перемещения которых в некоторых направлениях пространства ограничены другими объектами. Тела, ограничивающие свободу перемещения данной точки или тела, называются связями, наложенным на данную точку или тело. Несвободные материальные тела, нагруженные силами, действуют на связи силами, стремящимися эти связи преодолеть. Эти силы иногда называют - силы давления на связь. В соответствии с аксиомой статики о равенстве действия и противодействия, связи противодействуют возможному перемещению тела. Силы, с которыми связи действуют на рассматриваемый объект, называются силами реакций связей или реакциями связей, которые приложены к объекту в точке его соприкосновения со связью. Направление реакции связи противоположно тому, куда связь не дает перемещаться объекту.
Сформулируем еще раз основные определения, касающиеся связей.
Связи – всë, что ограничивает перемещение данного тела в пространстве.
Реакция связи – сила, с которой данная связь действует на тело.
Принцип освобождаемости от связей
Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями.
Основные виды связей:
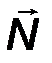
|
Рис.24
1. Гладкая опора. Это простой контакт тела с поверхностью, трением о которую можно пренебречь. Такая связь (рис.24) препятствует перемещению объекта только вдоль нормали к поверхности. Поэтому, реакция N такой связи перпендикулярна поверхности и носит название “нормальная реакция опоры”.
2. Невесомая нерастяжимая нить (трос, канат, цепь), (рис.25). Эта связь не дает перемещаться телу вдоль нити. Её реакция T приложена к телу, направлена вдоль нити к точке подвеса 0 и носит название “сила натяжения нити”.
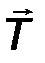
|
|
Рис.25
3. Цилиндрический шарнир, или подшипник (рис.26).
| 2 |
| 1 |
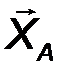
|
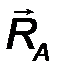
|
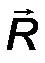
|
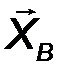
|
|
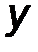
|
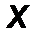
|
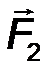
|
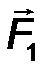
|
|
Рис.26
Цилиндрический шарнир - это устройство, запрещающее перемещение точек тела, принадлежащих оси шарнира и позволяющее осуществлять относительное вращение соединенных с его помощью тел в плоскости, перпендикулярной оси шарнира. Реакция R шарнира направлена в этой плоскости, т.е. перпендикулярна оси шарнира и имеет две ортогональные составляющие XA, YA. Математически её можно оценить по формуле:
| R A = √X 2 A + Y 2 A . | (21) |
4. Сферический шарнир (Рис.27). Такая связь допускает вращение тела в любом направлении в пространстве, но запрещает перемещение точки закрепления тела. Реакция RA может быть направлена в любую сторону и имеет три ортогональные составляющие XA, YA, ZA. Величина силы оценивается аналогично:
| RA = √X 2 A + Y 2 A + Z 2 A . | (22) |
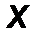
|
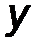
|
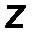
|
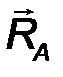
|
|
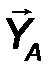
|
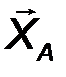
|
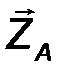
|
Рис.27
5. Невесомый шарнирно опертый стержень (рис.28). На стержень действуют лишь две реакции в шарнирах, приложенные к его концам. В покоящейся, уравновешенной системе, в соответствии с аксиомой статики, эти силы равны, противоположны и направлены по одной прямой, т.е. линии, соединяющей концы стержня при любой его форме (прямолинейной, криволинейной, ломаной):
RD = -RB .
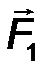
|

|
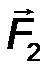
|
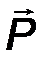
|
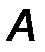
|
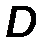
|
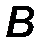
|
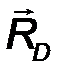
|
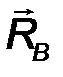
|
Рис.28
6. Жесткая заделка, или консоль. Это - балка с замурованным в стену концом, или гвоздь, вбитый в стену (рис.29). В заделке отсутствуют все перемещения линейные и угловые перемещения. Рассматривая плоской систему сил, в заделке возникает пара сил с моментом МА, препятствующая повороту балки и реакция RA с двумя ортогональными составляющим XA YA. Таким образом, в плоской консоли возникает два компонента реакции. Величина реакции определяется:
| RA = √X2A + Y2A . | (23) |
|
|
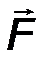
|
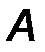
|
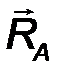
|
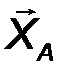
|
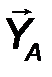
|
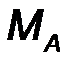
|
Рис.29
7. Подпятник (рис.30) – отличается от цилиндрического шарнира отсутствием возможности перемещения вдоль оси шарнира. Примером шарнира с подпятником может служить дверная или оконная петля. Такое ограничение приводит к появлению третьей составляющей реакции по оси 0Z.
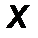
|
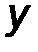
|
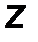
|
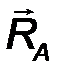
|
|
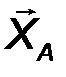
|
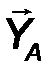
|
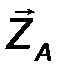
|
Рис.30
Реакция в подпятнике вычисляется по правилу геометрического сложения ортогональных векторных компонент:
| RA = √X 2 A + Y 2 A + Z 2 A . | (24) |
8. Подвижная шарнирная опора (рис.31).
Такая связь полностью идентична гладкой опоре. Линия действия реакции перпендикулярна опорной поверхности.
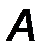
|
|
Рис.31
9. Тело опирается на неподвижную точку или гладкую линию (рис.32).
Реакция N A направлена по нормали к опирающейся поверхности.
10. Тело опирается точкой или гладкой линией (рис.32).
Реакции NВ и N с направлены по нормали к опорной поверхности.
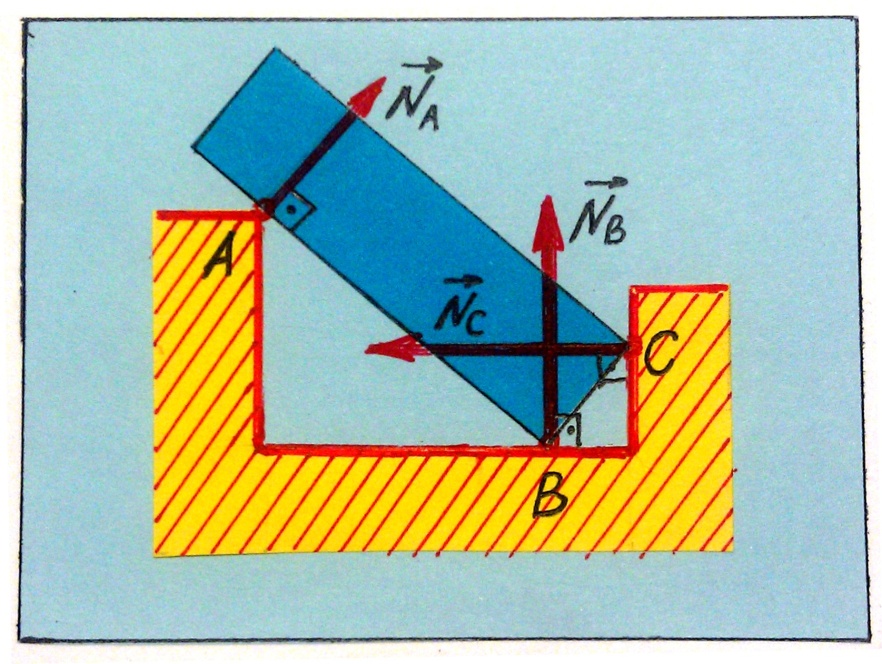
Рис.32
Дата: 2018-11-18, просмотров: 781.