Случай 1. Пусть дана произвольная система сил, для которой второй инвариант отличен от нуля: (RM0) ≠ 0, а следовательно , и первый инвариант отличен от нуля:
R ≠ 0.
Раскладываем главный момент на две составляющие: по направлению главного вектора и перпендикулярно главному вектору.
По существу пару с моментом M 0 раскладываем на две пары с моментами M 1П и M 2П , M 0= M 1П + M 2П (рис.36).
Для пары с моментом M 2П подберем плечо таким образом , чтобы модуль сил пары был равен модулю главного вектора. Это можно сделать на основании третьей теоремы об эквивалентных парах. На основании второй теоремы об эквивалентных парах эту пару повернем в ее плоскости так, чтобы одна из сил пары была направлена прямо противоположно главному вектору, т.е. пару с моментом M 2П представим так
R - R
O O
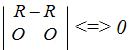
На основании второй аксиомы статики система сил
На основании третьей аксиомы статики ее можно отбросить. Таким образом, в этом случае произвольная система сил эквивалентна одной силе R и паре с моментом M 1П, коллинеарным силе R.
Запишем приведенное доказательство
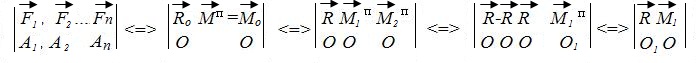
Определение 1. Совокупность силы и пары, момент которой коллинеарен силе, называется динамой или динамическим винтом.
По определению MП = pR, где p- параметр динамы.
Различают правую динаму p>0 (рис.37) и левую динаму p <0 (рис.38).
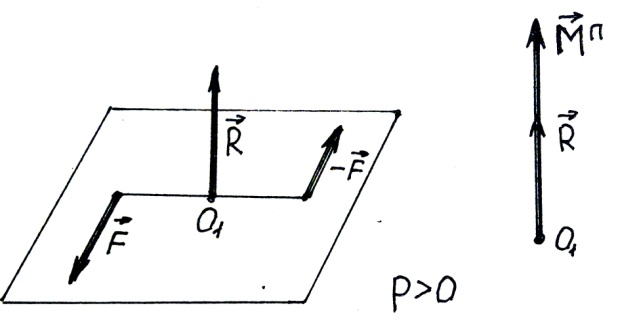
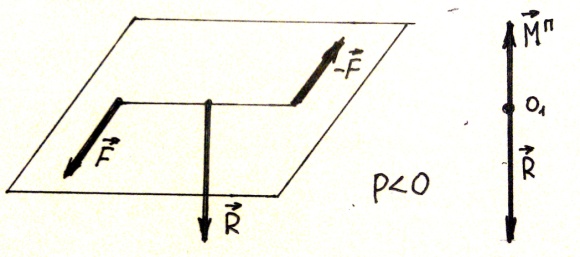
Рис.37 Рис.38
Определение 2. Центральной осью произвольной системы сил называется геометрическое место центров приведения, относительно которых главный момент коллинеарен главному вектору или равен нулю.
MN = pR.
Согласно этому определению точка О1 принадлежит центральной оси. Если взять любую точку N, которая находится на линии действия главного вектора R, проходящего через точку О1 , то эта точка N  также будет принадлежать центральной оси, так как главный момент относительно этой
также будет принадлежать центральной оси, так как главный момент относительно этой
точки будет равен
M N = M 0 - M П2 .
Следовательно, если второй инвариант произвольной системы сил отличен от нуля, то такая система сил приводится к динаме, расположенной вдоль центральной оси.
Уравнение центральной оси произвольной системы сил
При приведении произвольной системы сил к точке О мы получили главный вектор R и пару с моментом MП = M 0 .
Выберем систему координат О XYZ.
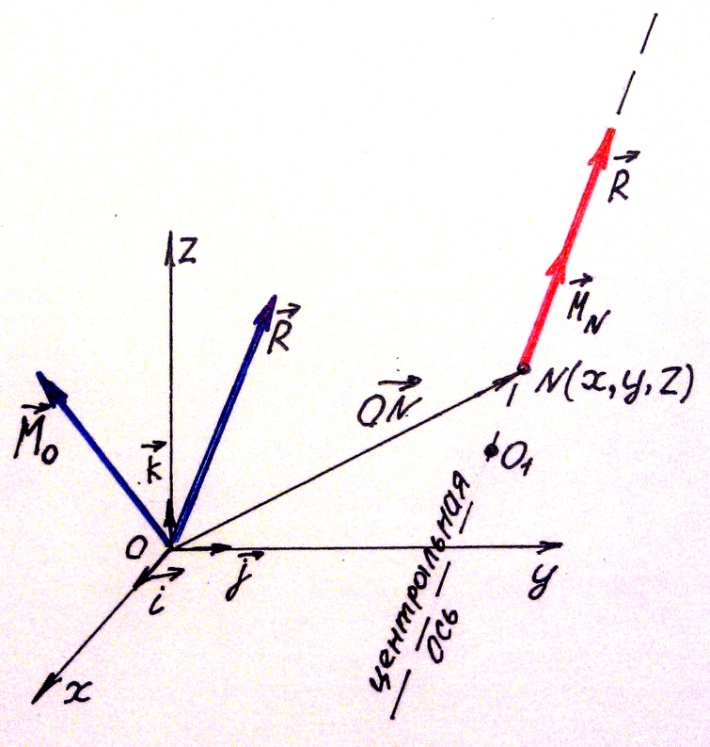
Рис.39
Возьмём произвольную точку N(x,y,z) на центральной оси (рис.39). Из определения центральной оси следует MN = pR. Запишем зависимость между главными моментами произвольной пространственной системы сил относительно двух точек O и N.
M o = M N +[ ON ∙ R ], откуда MN = M o - [ ON ∙ R ].
С другой стороны, M N = PR, следовательно, Mo-[ ON ∙ R] = pR ,
где Mo = M x i + M y j + M z k .
Векторное произведение и [NO ∙ R] запишем в виде символического определителя третьего порядка
i j k
M x i + M y j + M z k - x y z =pR .
Rx Ry Rz
Спроецируем последнее равенство на оси координат.
M x- ( yR z- zR y) = pR x; M y - ( zR x- xR z) = pR y; M z - ( xR y- yR x) = pR z.
Предполагая, что RX, RY и RZ отличны от нуля, и поделив последние равенства соответственно на R X, RY и RZ получим,
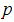 M x-( yR z- zR y) M y-( zR x- xR z) Mz-( xR y- yR x) (30)
M x-( yR z- zR y) M y-( zR x- xR z) Mz-( xR y- yR x) (30)
R x R y R z
Это уравнение является уравнением центральной оси произвольной системы сил.
Случай 2. Пусть произвольная система сил такова, что первый инвариант отличен от нуля, а второй инвариант равен нулю : 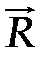
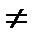 0, (
0, ( 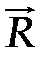
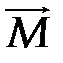
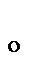 ) = 0.
) = 0.
Это возможно в двух случаях:
а) M 0 = 0.
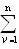 Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R = F v, проходящей через точку О.
Если M 0 = 0, то система сил эквивалентна одной силе, равной сумме всех сил системы и проходящей через точку О, т.е. система сил приводится к равнодействующей R = F v, проходящей через точку О.
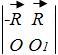 б) M0 ≠ 0, M 0
б) M0 ≠ 0, M 0 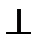 R .
R .
Если M 0 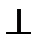 R то пару с моментом M 0 можно представить как,
R то пару с моментом M 0 можно представить как,
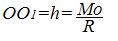
где ..
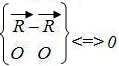
Так как система , то ее можно отбросить. Следовательно, система
сил 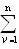 будет эквивалентна одной силе, проходящей через точку О 1, т.е. система сил
будет эквивалентна одной силе, проходящей через точку О 1, т.е. система сил
приводится к равнодействующей R= F, проходящей через точку О 1.
Итак, если первый инвариант отличен от нуля, а второй инвариант равен нулю, то произвольная система сил приводится к равнодействующей, расположенной вдоль центральной оси.
Случай 3. Пусть произвольная пространственная система сил такова, что главный вектор равен нулю и главный момент относительно произвольной точки отличен от нуля R = 0, M 0 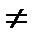 0. Очевидно, что в этом случае система сил приводится к паре сил, причем MП= M 0 .
0. Очевидно, что в этом случае система сил приводится к паре сил, причем MП= M 0 .
Случай 4. Если произвольная пространственная система сил такова, что главный вектор равен нулю и главный момент относительно произвольной точки равен нулю
R = 0, M 0 = 0, то она находится в равновесии. Эти условия будут как достаточными, так и необходимыми для равновесия.
Сводная таблица результатов приведения пространственной системы
сил к простейшему (каноническому) виду
| Математические характеристики системы сил, приложенной к свободному абсолютно твердому телу | Заключение о системе сил | |
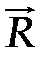 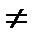 0 0
| ( 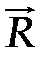 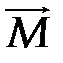  ) ) 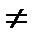 0 0
| Система сил приводится к динаме |
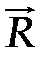 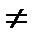 0 0
| ( 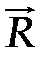 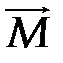 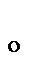 ) = 0 ) = 0
| Система сил приводится к равнодействующей, приложенной
в точке О или О 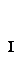
|
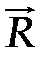 =0 =0
| 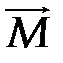 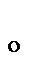 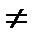 0 0
| Система сил приводится к паре сил |
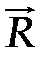 =0 =0
| 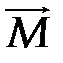 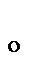 = 0 = 0
| Система сил эквивалентна нулю, т.е. находится в равновесии |
5.5. Алгоритм решения задач на приведение пространственной системы сил к простейшему (каноническому) виду
1. Изобразить в масштабе и обозначить все силы, приложенные к материальному объекту.
2. Выбрать оси декартовой прямоугольной правой системы координат O xyz.
3. За центр приведения принять начало координат т. O.
4. Вычислить проекции главного вектора системы сил на оси координат, найти его модуль и направляющие косинусы. Изобразить на рисунке в масштабе, приложив в точке О.
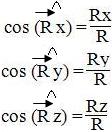
| RX = ∑X ; ; RY = ∑Y ; ; RZ = ∑Z ; ; | ||
| R = √R2 X + R2 Y + R2 Z . |
5. Вычислить главные моменты системы сил относительно координатных осей x, y, z , начала координат т. O., и направляющие косинусы главного момента Mo. Изобразить их на рисунке в масштабе, приложив в точке О.
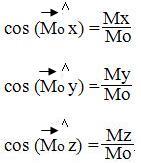
MX = ∑momX F , ;
MY = ∑momY F , ;
MZ = ∑momZ F , ;
M 0 = √M 2 X + M 2 Y + M 2 Z .
6. Вычислить величину второго инварианта и определить, к какому
простейшему виду приводится данная система сил:
( RM o) = R x M x + R y M y + R z M z = …
7.Вычислить наименьший главный момент системы сил
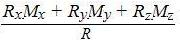
M 1П = = …
Если система сил приводится к динаме или к равнодействующей,
то далее найти уравнение центральной оси (30.). Затем определить
(если это необходимо) точки пересечения центральной оси с
координатными плоскостями, построить эту ось и изобразить
динаму или равнодействующую вдоль центральной оси.
Дата: 2018-11-18, просмотров: 1212.