Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Главный вектор и главный момент произвольной пространственной системы сил

Произвольная пространственная система сил – это такая система сил, линии действия которой произвольно расположены в пространстве

Главный вектор пространственной системы сил определяется так же, как в плоской статике: это вектор R, равный векторной сумме всех сил системы:

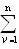
R = F 1 + F 2 + … F n = F n .

(25)

 

Модуль R главного вектора пространственной системы сил вычисляется по следующим формулам:

 

R = √R 2 X + R 2 Y + R 2 Z,

(26)

где

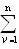
Rx = Xv = ∑x ; 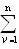Ry =  Yv = ∑y ;                                                                          (27) 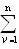Rz =   Zv = ∑z .

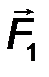
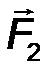
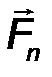
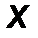
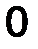
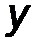
1

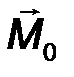
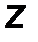
2

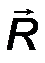
Рис.33

Главным моментом системы сил называется вектор M ₀, равный сумме  моментов (векторных) всех сил, вычисленных относительно некоторого центра (точки О) (рис.33):

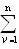
M 0 =    mom 0 F v .

(28)

 

Вектор R не зависит от выбора центра О, а вектор M₀ при изменении положения центра О может в общем случае изменяться.

Величина главного момента M₀ системы сил относительно центра O (начала координат) и его проекции на оси координат вычисляются по формулам:

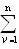
MX = momX F v ; 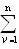MY = momY F v ; 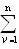MZ = momZ F v ;   M0 = √M 2X + M 2Y + M 2Z.

(29)

 

Для простых случаев проекции главного момента системы сил относительно координатных осей и начала координат  могут определяться геометрически.

Пример.

К вершинам куба (рис.34) с длиной ребра a приложена система четырех сил, действующих вдоль ребер куба и имеющих одинаковые модули: F₁=F₂=F₃=F₄=F.

Определить главный вектор этой системы сил и её главный момент относительно вершины О.

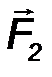
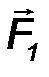
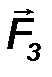
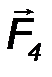
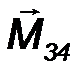
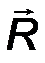
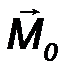
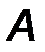
Рис.34.

Решение. Выберем декартову прямоугольную правую систему координат O _xyz, оси которой ориентированы вдоль ребер куба.

Силы F ₃, F ₄ образуют пару сил с моментом M ₃₄, направленным в положительном направлении оси Ox (точка приложения вектора M ₃₄ может быть выбрана произвольно) и равным по модулю M ₃₄ = F·a. Следовательно, силы F ₃ и F ₄ можно не учитывать при вычислении проекций главного вектора R.

 

Вычислим проекции главного вектора R на оси координат и его модуль:

 

R_X = F _1x + F _2x = 0 - F ₂ = -F;

R_Y = F _1y + F _2y = 0;

R_Z = F _{1 z} + F _{2 z} = F + 0 = F .

R = ( R_X + R_Y + R_Z )^1/2 =√2 F .

 

Определим геометрически проекции главного момента M ₀ на оси координат (напомним, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости), проецируя на оси координат M ₃₄:

 

M_X = M_X( F ₁ ) + M_X( F ₂ ) + ( M ₃₄ )_X= 0 + 0 + M₃₄ = F a;

M_Y = M_Y( F ₁ ) + M_Y( F ₂ ) + ( M ₃₄ )_Y = 0 + 0 + 0 = 0;

M_Z = M_Z( F ₁ ) + M_Z( F ₂ ) + ( M ₃₄ )_z = 0 + F·OA + 0 = F a;

Модуль главного момента равен:

 

                                M ₀ = √ M ² _X + M ² _Y + M ² _Z =√2 F· a.

 

Таким образом, для заданной системы сил её главный вектор R и главный момент M ₀ относительно точки О равны по модулю R=√2 F; M₀=√2 F·a, лежат в плоскости Oxz и образуют с осью Oz углы в 45° (см. рис.34).

 

5.2. Теорема о приведении произвольной пространственной системы сил

 

Под приведением в механике понимают замену данной системы сил простейшей ей эквивалентной.

Произвольная пространственная система сил, действующих на абсолютно твердое тело, эквивалентна в общем случае силе, равной сумме всех сил системы и приложенной в произвольно выбранном центре приведения и паре сил, момент которой равен сумме моментов всех сил системы вычисленных относительно этого центра приведения.

Доказательство.

Пусть произвольная пространственная система сил:

 

                                                    F1 , F2 … Fn

A1, A2 … An .

 

приложена к абсолютно твердому телу (рис.35). Примем произвольную точку О за центр приведения. В точке О на основании второй и третьей аксиом статики добавим  к данной системе сил уравновешенную систему сил подобную данной. Силы, приложенные в точке О, образуют систему сходящихся сил, которую в общем случае приводим к одной силе, равной их сумме. Оставшиеся силы образуют n пар сил, действия которых заменяем одной парой с моментом, равным сумме моментов этих пар.

      

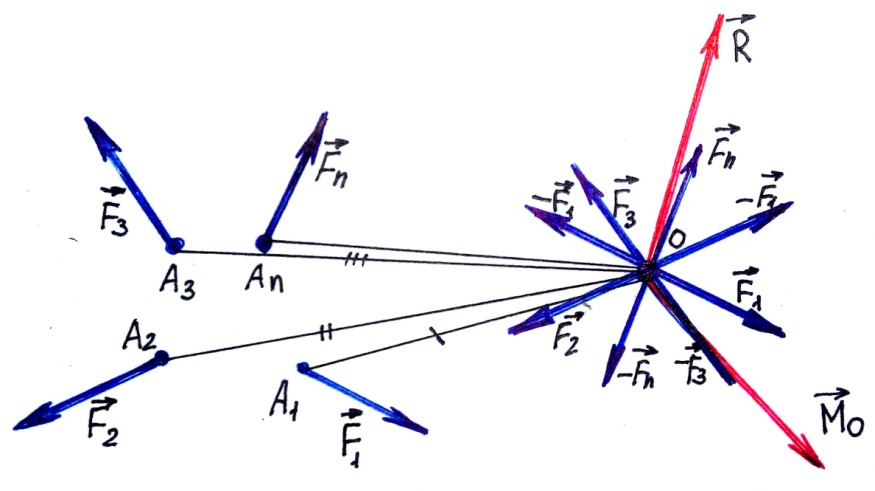
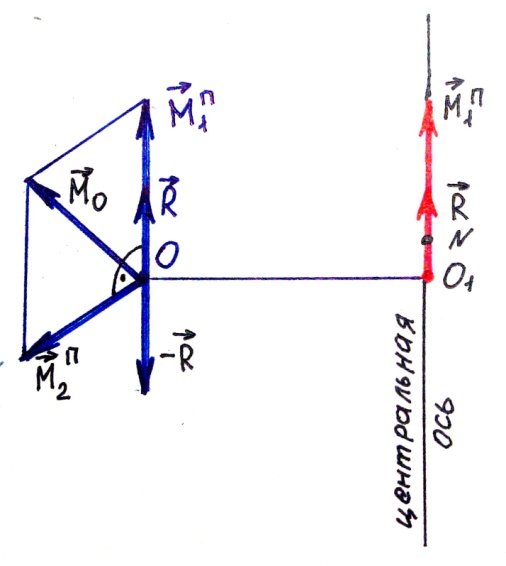
                              Рис.35                                                           Рис.36

 

Запишем приведенное доказательство:

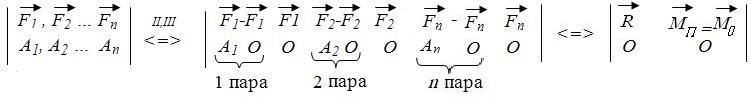
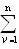
R = F ₁ + F ₂ + … F _n = F _v     -  главный вектор.

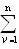
M^П=   mom₀ F _v = M ₀    -  главный момент.

5.3.Инварианты произвольной системы сил

Величины, которые остаются неизменными при каком-либо преобразовании, называются инвариантами по отношению к этому преобразованию.

Под инвариантами системы сил  понимают величины, которые не изменяются при перемене центра приведения этой системы.

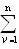Первый инвариант – векторный инвариант - главный вектор произвольной системы сил не зависит от выбора центра приведения.

R = F _v.

Второй инвариант – скалярный инвариант – скалярное произведение главного вектора на главный момент, вычисленный относительно произвольной точки не зависит от выбора центра приведения.

( R M_N) = ( RM_M) .