Для спектральной плотности энергии W (ω) справедливы соотношения:

                                                                                                                                 (13.1)

При τ = 0 для корреляционной функции будем иметь

                                                                                                                                 (13.2)

Выражение (45) представляет равенство Парсеваля.

Каждая из частей этого равенства определяет энергию сигнала. Как следует из (13.2) энергия сигнала численно равна площади под кривой W (ω).

Кривая W (ω) характеризует распределение энергии сигнала по частоте.

На практике x(t) задается на интервале конечной длины T, так что S(ω) оценивается по финитному преобразованию Фурье.

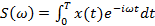                                                                                     (13.2)

Важнейшей характеристикой спектрального анализа является частотное

 разрешение, позволяющее разделить в спектре близкие по частоте гармонические составляющие анализируемого сигнала. Частотное разрешение определяется шириной Δω полосы спектра, которая связана с длительностью реализации T соотношением Δω = 2π/T .

Иногда вместо круговой частоты ω (радианы, деленные на единицу времени) удобнее использовать физическую частоту f (число периодов на единицу времени), измеряемую в Гц. Тогда прямое и обратное преобразование Фурье принимают вид:

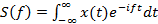                                                                                (13.3)

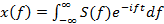                                                                                   (13.4)

Сравнение спектров периодического сигнала, имеющего период T, с непериодическим сигналом в той же полосе частот Δω и одинаковой длительности позволяет связать 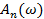 и S (ω) следующим образом:

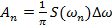                                                                                                (13.5)

где .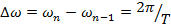

Современные средства спектрального анализа сигналов используют преобразования Фурье в дискретной форме (ДПФ). Для получения дискретной функции времени надо подвергнуть процессу дискретизации непрерывную функцию времени, т. е. из сигнала x (t) на интервале 0 . . . T берется N равноотстоящих отсчетов. При спектральном анализе требуется определить шаг по частоте и максимальную частоту спектра (частота Найквиста). Общая длина реализации для вычисления преобразования Фурье определится так:

                                            ,                                                                (13.6)

тогда максимальная частота спектра

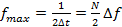                                                                                                     (13.7)

Следовательно, шаг по частоте можно определить по формуле:

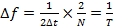                                                                                               (13.8)

Произведя замену параметра T на количество отсчетов N и обозначив

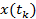 как 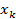(k = 0, . . . ,N − 1), с учетом 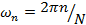, прямое и обратное

преобразование Фурье можно представить в виде

                                                                                                                                 (13.9)

Для вычисления ДПФ целесообразно использовать быстрое преобразование Фурье (БПФ, FFT) — алгоритм вычисления за количество действий, меньшее, чем требуемых по формуле ДПФ.

Одно из условий применимости дискретного преобразования Фурье — использование антиалайзингового фильтра для ограничения верхней граничной частоты преобразуемого сигнала, которая не должна быть выше половины от частоты его дискретизации. Если частотный диапазон сигнала шире указанного, то при отсутствии антиалайзингового фильтра происходит искажение спектра сигнала, в котором появляются ложные составляющие.

Спектральный анализ используется для разделения сигналов на простейшие составляющие в частотной области. Он эффективен прежде всего в тех случаях, когда сигналы имеют аддитивные периодические компоненты.

Вибрационная диагностика имеет еще одну существенную область применения спектрального анализа — разделение на простейшие частотные составляющие сложных сигналов, являющихся произведением двух стационарных компонентов, хотя бы один из которых содержит периодические составляющие. Подобную сложную структуру имеют многие колебательные силы во вращающемся оборудовании, и для обнаружения отдельных видов дефектов необходимо по сигналу вибрации определять параметры мультипликативных составляющих колебательных сил. Сначала необходимо выполнить операции выделения из измеряемой вибрации мультипликативных компонентов одной природы, затем операции разделения их на стационарные сомножители и лишь после этого проводить спектральный анализ того из них, который содержит периодические составляющие.

Преобразования Фурье являются универсальным математическим аппаратом, связывающим сигналы во временной и частотной областях. Особенностью этих преобразований является то, что применение прямого и обратного преобразования к вещественному сигналу дает одинаковые, с точностью до множителя, результаты.

При решении ряда диагностических задач может использоваться еще один вид анализа вибрации — взаимный спектральный анализ двух сигналов, измеренных в разных точках контроля и(или) в разных направлениях. Взаимный спектр представляет собой произведение комплексно сопряженного спектра сигнала, измеряемого в одной точке, на комплексный спектр сигнала, измеряемого в другой точке.

Взаимная спектральная плотность сигналов равна

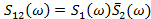                                                                                    (13.10)

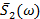- комплексно сопряженная спектральная составляющая второго сигнала.

Модуль и фазовый угол определяются соотношениями

                                                                                                                               (13.11)

                                                                                                                               (13.12)

Формулы (13.11) и (13.12) определяют взаимный спектр амплитуд и фаз соответственно. Спектр амплитуд характеризует энергетическое взаимодействие гармонических компонент двух процессов, а спектр фаз — временной сдвиг между компонентами.

Функция когерентности 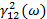 определится так:

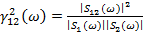                                                                                      (13.13)

Она является аналогом коэффициента корреляции в частотной области и отражает степень линейной связи взаимосвязи гармонических компонент рассматриваемых процессов.

Кроме спектров взаимной мощности в некоторых задачах, связанных с определением форм колебаний машин и оборудования, могут использоваться и фазовые взаимные спектры. Однозначность полученных из такого спектра разностей фаз 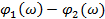 имеет место лишь в диапазоне углов от –π до +π и в том случае, если составляющие вибрации в точках контроля на частоте имеют высокую степень когерентности. Поэтому в большинстве практических случаев фазовые взаимные спектры строятся только для составляющих с коэффициентом когерентности выше порогового, обычно выбираемого на уровне 0,7.

Спектр колебаний, изображенный графически, называется спектральной диаграммой. Амплитудная спектральная диаграмма образуется при построении на плоскости в прямоугольных координатах, по оси абсцисс которых откладывается частота (или номер) гармоники, а по оси ординат соответствующая этой частоте амплитуда гармоники. Фазовая спектральная диаграмма начальных фазовых углов получается таким же построением в координатах «частота (номер гармоники)– начальный фазовый сдвиг».

Следует подчеркнуть, что среднеквадратическое значение периодической вибрации не зависит от значений измерений фазовых углов гармоник, содержащихся в вибрационном процессе, в то время как изменение начальных фазовых углов гармоник полигармонической вибрации, приводящее к изменению его формы, сопровождается изменением пикового значения размаха и среднего значения вибрации.