Для широкополосных сигналов автокорреляционная функция сконцентрирована вблизи начала координат (τ = 0), для низкочастотного сигнала отлична от нуля на значительном участке оси τ. Она несет большую информацию о вибросигнале.

Очевидно соотношение

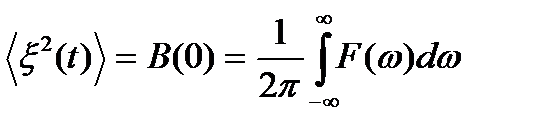                                                                           (14.1)

Спектральная плотность мощности случайного процесса выражается через обычный спектр Фурье укороченной реализации ξ (t) в промежутке [−T, T]

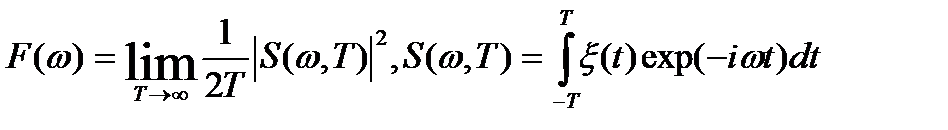                                       (14.2)

Важное место в спектральной теории случайных процессов занимает теорема Винера–Хинчина. Функция автокорреляции B(τ) случайного сигнала ξ(t) и его спектральная плотность мощности F(ω) связаны между собой парой взаимного преобразования Фурье, называемых формулами Винера–Хинчина.

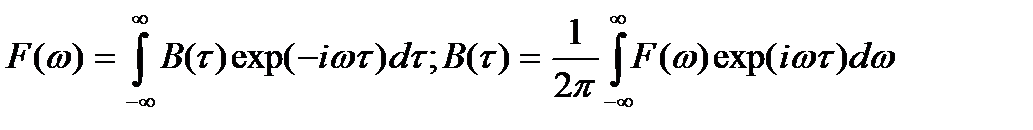                               (14.3)

Отсюда следует, что теорему Винера–Хинчина можно рассматривать также как определение понятия спектральной плотности мощности случайных процессов.

Если случайный процесс имеет отличное от нуля математическое ожидание 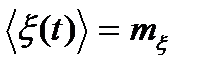, то в выражении спектральной плотности появляется дополнительное дельтаобразное слагаемое 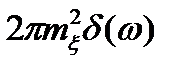, что соответствует появлению в спектре дискретной линии на нулевой частоте. Спектральная плотность является неотрицательной F (ω) > 0 и четной F (ω) = F (−ω) функцией своего аргумента.

Учитывая четность спектральной плотности, формулы Винера–Хинчина можно также записать в виде

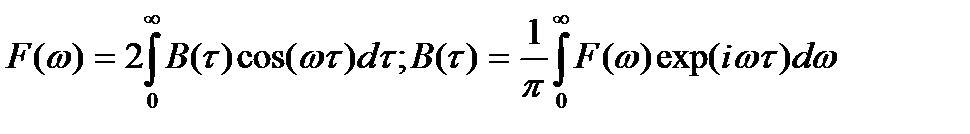                                     (14.4)

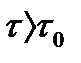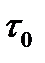Если значения сигнала отличаются на временной интервал , где  — интервал корреляции, то для стационарных случайных сигналов со средним значением  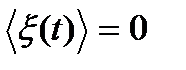эти значения считаются независимыми, и B(τ) стремится к нулю.

Таким образом, автокорреляционная функция стационарного случайного сигнала дает два информативных параметра: 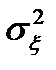 — мощность сигнала и  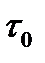— интервал корреляции.

В большинстве практических случаев сигнал вибрации машин и оборудования содержит как случайные, так и детерминированные составляющие, причем случайные составляющие могут определять мощность сигнала преимущественно на высоких частотах. Корреляционный анализ таких сигналов проводится лишь для высокочастотных компонентов, предварительно выделенных полосовым фильтром.

На практике протяженность спектральной плотности характеризуется шириной полосы спектра — 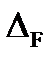. Она определяется как величина площади под кривой спектральной плотности, отнесенной к спектральной плотности на характерной частоте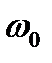

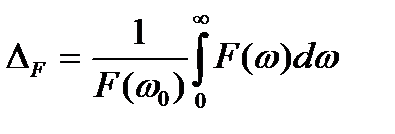                                                                                            (14.5)

В качестве 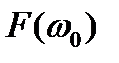 принимают максимум спектральной плотности или координату, соответствующую точке симметрии. Обычно при широкополосном спектре это спектральная плотность на нулевой частоте F (0). Следует отметить, что произведение интервала корреляции  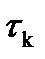на ширину полосы  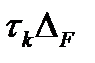— величина постоянная для семейства спектральных плотностей заданной формы, т. е. чем уже корреляционная функция, тем протяженнее спектр, и наоборот, чем протяженнее корреляционная функция, тем уже спектр.

Для полного описания вибрационного поля технической системы недостаточно знать характеристики сигналов в отдельных точках, поэтому используют их совместные характеристики, отражающие статистическую связь вибраций в различных участках. С практической точки зрения наиболее важными пространственными характеристиками являются зависимость коэффициента корреляции в разных точках поля от расстояния между точками и интервал корреляции.

Взаимной спектральной плотностью мощности называется ее Фурье преобразование взаимной корреляционной функции

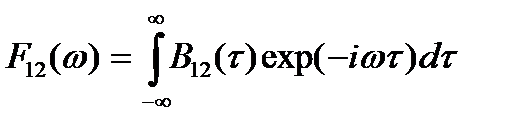                                                                               (14.6)

Имеет место и обратное преобразование

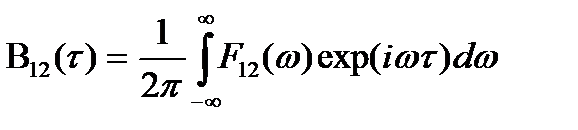                                                                          (14.7)

Аналогично коэффициенту корреляции, удобной характеристикой является нормированная взаимная спектральная плотность мощности двух сигналов

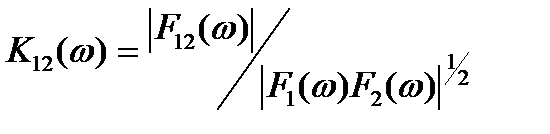                                                                             (14.8)

которая называется функцией когерентности.

Физический смысл этой характеристики сигналов тот же, что и у коэффициента корреляции, — это мера линейной пропорциональности связи между сигналами. Однако узкополосность функции когерентности обуславливает одну ее отличительную особенность, которая в ряде случаев оказывается весьма важной при анализе сигналов. Это связано с тем, что широкополосный сигнал, распространяясь по конструкции, искажается настолько, что, несмотря на линейную связь, перестает коррелировать со своим первоначальным видом, в то время как функция когерентности не изменяется и сигнал при распространении по сложным конструкциям не перестает быть когерентным.

Следует отметить, что автокорреляционная функция несет информацию в первую очередь о наиболее сильных частотных компонентах сигнала. Для того чтобы поднять значимость слабых частотных компонентов сигнала, применяют преобразование Фурье не к спектральной плотности мощности, а к ее логарифму. При этом исторически сложилось так, что к логарифму спектральной плотности стали применять не обратное, а прямое преобразование Фурье, назвав такую операцию кепстральным преобразованием. В результате получается функция, имеющая размерность времени по оси ординат и не имеющая размерности по оси абсцисс. Новые переменные назвали соответственно сачтотой τ и маплитудой G, а сам результат преобразования — кепстром мощности.

Кепстра мощности сигнала x(t) — это энергетический спектр функции 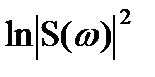, определяемый выражением

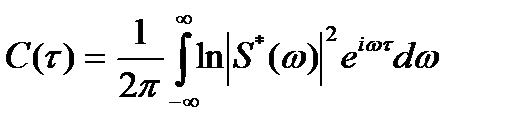                                                                              (14.9)

где 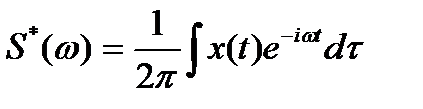, τ — кепстральное время (τ называют «сачтота» или «квефренсия» — аналоги от русского слова «частота» или английского «frequency»).

Кепстр имеет смысл не для любых функций, а лишь для тех, которые имеют ограниченный спектр. Для тех же функций, спектр которых неограничен, для возможности практического использования кепстрального метода, вводят ограничение по частоте ±2ω, внутри которого заключается основная доля энергии сигнала.

Комплексный кепстр определяется выражением

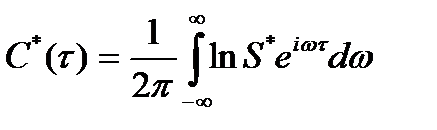                                                                                      (14.10)

Термин «кепстр» образован перестановкой букв в слове «спектр».

Другая версия — термин «кепстр» связан с именем крупнейшего математика А.Н.Колмогорова. Им был предложен специальный функциональный ряд для обработки регулярных стационарных случайных процессов. Это слово по первым буквам «Kolmogorov Equation Power Series Time Response». Кепстр мощности — неотрицательная функция времени, но в отличие от функции автокорреляции становится отличным от нуля в случаях, когда появляются большие неоднородности функции F(ω), т. е. он чувствителен не ко всем неоднородностям спектра F(ω), а только к тем, которые обусловлены периодически следующими один за другим сигналами.

Комплексный кепстр позволяет преобразовывать назад в исходный сигнал во временнґую область, в то время как кепстр мощности допускает лишь обратное преобразование в спектр мощности. Следует отметить, что в диагностических задачах чаще вместо комплексного кепстра предпочитают работать с кепстром мощности или действительным кепстром, пренебрегая информацией о фазе, содержащейся в спектрах. Кепстр мощности тесно связан с автокорреляционной функцией: если не производить предварительное логарифмирование спектра, то та же самая процедура расчета даст автокорреляционную функцию. Горизонтальная ось кепстра имеет размерность времени, однако не является временем в обычном смысле. Оно может быть названо периодическим временем.

Кепстр сходен по форме с обратным преобразованием Фурье: он возвращает спектральное описание процесса — спектральную плотность — во временную область, но несколько измененным образом: логарифм, как слабо меняющаяся функция аргумента, сглаживает случайные, непериодические составляющие процесса, подчеркивая периодические за счет умножения на косинус.

В знак того, что кепстр не есть исходный сигнал, аргумент кепстра τ носит название сачтота, максимумы на зависимости кепстра от сачтоты называют рагмониками — от harmonics (гармоника), а сам кепстр иногда называют псевдокорреляционной (т. е. как бы корреляционной) функцией. Область применения кепстра определяется основными особенностями графика его зависимости от квефренсии, в первую очередь наличием максимумов, положение которых соответствует основным периодам гармонических рядов (не отдельных гармоник, а целых их рядов). Высота этих максимумов определяется суммарной амплитудой всех гармонических составляющих для данного гармонического ряда.

Кепстр используют для формирования диагностических признаков в тех случаях, когда колебательный процесс имеет периодически модулированный спектр, что может наблюдаться при явлениях нелинейного взаимодействия узлов и деталей механизма, при наличии амплитудной или частотной модуляции, а также при преобразованиях типа свертки нескольких временных процессов.

В качестве диагностических признаков используют амплитуды кепстральных компонент. Он служит для выделения периодических составляющих процесса в случае, когда число их больше единицы. Диагностическими параметрами, которые позволяет получить кепстр являются значения квефренсии (сачтоты), на которых имеются максимумы, амплитуды рагмоник, соотношения между указанными параметрами.

Полезность кепстра заключается в том, что он выделяет периодичности, или повторяющиеся структуры, в спектре, точно так же, как спектр выделяет периодичности из временнґой реализации. Часто спектр роторных машин является очень сложным и содержит несколько наборов гармоник от различных узлов и несколько наборов боковых полос, вызванных различными модуляциями.

Кепстр такого спектра будет иметь пики, соответствующие расстояниям между гармониками и боковыми полосами, и их будет значительно легче различить и идентифицировать. Однако в некоторых случаях, например, при повреждении роликов подшипника уровни гармоник и боковых полос уменьшаются по мере приближения к сильным степеням разрушения. По отношению к спектру, кепстр является таким же сжатием данных, как сам спектр по отношению к временной реализации. Преобразование Фурье от логарифмического спектра мощности, т. е. кепстр позволяет разделить во времени информацию о сигнале, полученную в результате многократных отражений, при нелинейных преобразованиях и модуляции. При этом энергия виброакустического сигнала, рассеянная по множеству гармоник в спектральном представлении, локализуется в одной составляющей в кепстральном представлении сигнала.

Кепстральный анализ сигнала реагирует на периодичность в его спектре и поэтому позволяет определить длительность импульса и расстояние между импульсами. Для оценки возможности применения кепстрального анализа в простейших случаях достаточно одного и последовательности из двух импульсов (рис. 14.1). Здесь показаны модули кепстральных составляющих.

Отсюда видно, что кепстральный анализ позволяет определить и длительность импульса Δt (составляющие кепстра с сачтотами Δt/k) и расстояние между импульсами ΔT.

Более подробное рассмотрение возможности кепстрального анализа показывает, что при анализе периодических сигналов он реагирует на отличие формы сигнала от гармонической и, в первую очередь, на импульсные сигналы.

Импульсный характер имеет вибрация, возбуждаемая периодическими ударами в машинах возвратно-поступательного действия, а также в подшипниках качения. имеющих некоторые виды дефектов. Спектр такой вибрации также имеет периодический характер, что отражается и в форме кепстра. Кепстральный анализ позволяет обнаружить слабые периодические ударные импульсы в низкочастотной вибрации машины, но при этом дает лишь качественный анализ этих импульсов. Основной областью применения кепстрального анализа сигналов вибрации является обнаружение и исследование групп периодических импульсов, например, импульсных тестовых сигналов и их отражений (эхо-сигналов).  Рис. 14.1. Формы одиночного и парного импульса (а), их спектры (б) и кепстры (в)

Существует ряд диагностических задач, когда требуется измерять и анализировать АЧХ механической системы, возбуждая ее вибрацию колебательными силами изменяющейся частоты. И в этом случае используются методы синхронного частотного анализа вибрации, а результатом анализа является зависимость величины амплитуды и фазы определенной составляющей вибрации от изменяющейся в заданном диапазоне частоты колебательной силы. Такой вид анализа чаще всего применяют для изучения низкочастотных резонансов машин с узлами вращения.

Спектральный анализ огибающей вибрации анализирует среднеквадратичные значения высокочастотной вибрации одной природы.

Большинство задач пространственного анализа вибрации связано с определением формы колебаний машин и оборудования или координат дефектов в протяженных системах, например, трубопроводах. Групповой анализ параметров сигнала вибрации чаще всего используют для определения пороговых значений в диагностических моделях.

Вибрация машин может иметь широкий спектр частот от нескольких герц до сотен килогерц. На основе результатов только широкополосных измерений нельзя выявить появление и развитие соответствующего дефекта до того, как увеличивающаяся амплитуда определенной гармоники достигнет величины, способной заметно изменить общий уровень вибрации. Поэтому для удобства измерения и анализа весь частотный диапазон вибрации делят на полосы. Для реализации возможности узкополосного анализа применяют аппаратурный или алгоритмический (на основе быстрого преобразования Фурье) методы.

При использовании аппаратурного метода из всего частотного диапазона с помощью соответствующих фильтров выделяют полосы частот с относительно постоянной шириной. Применяют декадные, октавные и третьоктавные полосы частот. Верхняя и нижняя граница декадных полос отличается в 10 раз, октавных — в 2 раза, третьоктавных — в 1,26 раза. При разделении частотного диапазона на полосы результаты измерения относят к среднегеометрическим частотам, которые для октавных полос находят из выражения

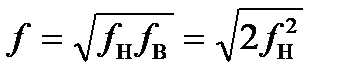                                                                                             (14.11)

Графическое представление среднеквадратического значения параметра вибрации в октавных или третьоктавных полосах частот называется соответственно октавным или третьоктавным спектром вибрации, изображенным в виде гистограммы. Иногда ширину диапазона измеряют в процентах от частоты середины диапазона. Используют узкополосные спектры с шириной диапазона 1,5; 3; 6 %. Для выполнения спектрального анализа на основе алгоритмического метода применяют цифровые виброанализаторы, использующие быстрое преобразование Фурье (БПФ). БПФ работает с выборками сигнала, равными по длине 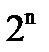, где n — целое число, принимаемое равным 9,. . . ,11, т. е. длина выборок равна 512, . . . , 2048 отсчетам. Все составляющие вибросигнала, попадающие в выборку, приводятся к некоторому среднему значению, отражаемому на спектре.

Преимуществом анализа в полосах частот с относительно постоянной шириной является возможность представления на одном графике широкого частотного диапазона с достаточно узким разрешением на низких частотах.

Разрешение в области высоких частот ухудшается при этом с повышением частоты. При использовании БПФ-анализаторов весь частотный диапазон разбивается на полосы с постоянной абсолютной шириной. При этом частотное разрешение постоянно во всем диапазоне.