Большинство колебательных процессов, с которыми приходится встречаться на практике, носит в той или иной степени случайный характер, при этом текущие значения процесса могут быть определены лишь с некоторой вероятностью. Поэтому в вибродиагностике приходится иметь дело со случайными величинами, изменяющимися во времени. Такие случайные величины являются функциями двух переменных: элементарных исходов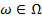 
и времени 
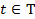. Вещественная числовая функция ξ (ω, t) двух переменных ( 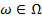, 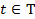) называется случайной функцией. Если T приписывается смысл времени, то ξ (ω, t) называют случайным процессом. Если фиксировать элементарный исход ω = ω0, то получится числовая функция вещественной переменной
ξ(ω0, t) = x (t), называемая реализацией случайного процесса. В дальнейшем для удобства ξ(ω, t) будем обозначать ξ(t). Если фиксировать какое-либо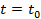 
, то значением случайного процесса в точке 
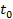окажется случайная величина. Эта случайная величина называется сечением случайного процесса.
Случайный процесс характеризуется распределением его сечений.
Случайный вибрационный сигнал описывается случайной функцией времени.
Так как текущие значения случайного колебательного процесса могут быть определены лишь с некоторой вероятностью, то процесс может быть представлен совокупностью статистических характеристик, постоянных или переменных во времени. Определить характеристики случайного процесса можно путем усреднения по ансамблю реализаций в определенные моменты времени.
Свойство инвариантности статистических характеристик относительно произвольного момента времени используется для классификации случайных колебательных процессов.
Случайные процессы делятся на стационарные и нестационарные.
Случайный стационарный процесс есть ансамбль реализаций, статистические характеристики которого инвариантны по отношению к переносу начала отсчета времени. Случайные стационарные колебания служат удобной моделью реальных процессов, свойства которых достаточно медленно изменяются во времени. Следует отметить, что на практике обычно не удается получить ансамбль реализаций требуемого процесса, по которому можно было бы вычислить эти статистические характеристики. Желательно оценивать все статистические свойства по одной реализации, заменяя усреднение по ансамблю усреднением по времени. Свойство, позволяющее такую замену осуществить, называют эргодичностью, и в этом случае случайные стационарные процессы называются эргодическими. Стационарный процесс будет эргодическим, если его статистические характеристики, полученные осреднением по ансамблю, с вероятностью, близкой к единице, равны тем же характеристикам, полученным осреднением по времени из любой достаточно длинной реализации случайного процесса. При нарушении этого условия колебательный процесс будет неэргодическим. Другими словами, эргодическим называется случайный стационарный процесс, для которого результаты усреднения по времени в пределах отдельной реализации одинаковы для всех реализаций. Таким образом, усреднение по времени для любой отдельной реализации эквивалентно соответствующему усреднению по ансамблю реализаций. Очевидно, что случайные эргодические процессы образуют очень важный класс случайных процессов, поскольку все свойства эргодических процессов можно определить по единственной выборочной функции.
Рассмотрим стационарный случайный процесс {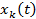 
}, где k = 1, 2, 3, . . . — номер реализации. Для любой реализации 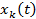среднее по времени значение статистической характеристики, например, средний квадрат, определяемый равенством
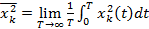(13.14)
Если процесс эргодический, то этот результат не должен зависеть от k и будет одним и тем же для всех реализаций. Соответствующее среднее по ансамблю реализаций значение определяется равенством
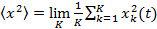(13.15)
Для эргодического процесса оба усреднения дают одинаковый результат.
С достаточной для решения практических задач точностью стационарные случайные компоненты сигналов вибрации машин и оборудования в установившихся режимах работы можно считать эргодическими.
На практике часто говорят о стационарности или нестационарности данных, представляющих собой единственную реализацию случайного явления.
В этом случае, если о единственной реализации говорят как о стационарной, то обычно имеют в виду, что ее свойства, определенные на коротких интервалах времени, существенно не изменяются от интервала к интервалу.
Здесь слово «существенно» означает, что наблюдаемые колебания превосходят отклонения, которые можно объяснить обычной выборочной изменчивостью статистических оценок.
Нестационарным называется случайный процесс, неудовлетворяющий условиям стационарности. Если не наложены дополнительные ограничения, то но зависят от времени и могут быть определены только путем усреднения в отдельные моменты времени по ансамблю выборочных функций, образующих процесс. На практике часто не удается получить достаточное для точной оценки характеристик процесса число реализаций, в связи с чем возникают трудности при анализе случайных нестационарных процессов.
Если случайная функция стационарна, то ее производная тоже стационарна по крайней мере в широком смысле. Более строго — мгновенные значения случайного процесса и его производной, взятые в один и тот же момент времени, являются некоррелированными величинами. Более того, если случайный процесс является гауссовым, то процесс и его производная статистически независимы. В [1] показано, что при суммировании хотя бы пяти-шести гармонических колебаний со случайными и взаимно независимыми фазами получается случайный процесс, близкий к гауссовому.
Если измеряемый параметр (виброперемещение) является стационарным, то его производные (виброскорость или виброускорение) могут приниматься также стационарными и некоррелированными без дополнительных проверок.
Точное математическое интегрирование стационарного процесса приводит к нестационарному процессу.
Во временной области случайный сигнал может быть описан с использованием вероятностных характеристик. Наиболее полными из них являются функции распределения вероятностей или плотность распределения вероятностей. В результате статистического анализа сложного сигнала вибрации можно дать количественную оценку отклонения реального распределения его значений от нормального. Существенные отклонения могут быть признаком наличия доминирующих компонентов в сигнале вибрации, возбуждаемых, например, ударными импульсами.
Формулы для вычисления математического ожидания случайного процесса при данных одномерных распределениях следуют из соответствующих формул для случайных величин. Пусть в сечении t случайного процесса непрерывная случайная величина x с плотностью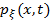 
, то математическое ожидание случайного процесса ξ(t) определится соотношением
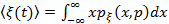(13.16)
Вибрация, как правило, имеет симметричные относительно равновесного положения значения, но при этом p(x) может иметь разную форму.
Под анализом вибрации принято понимать исследование функциональных зависимостей измеряемых параметров вибрации от одной или нескольких независимых переменных. Наиболее часто в качестве переменных используют время, частоту, пространственную координату или порядковый номер в группе независимых измерений вибрации.
При исследовании вибрации как функции времени чаще всего на практике анализируют форму временного сигнала вибрации, траекторию движения центра объекта, а также параметры плотности распределения вероятностей мгновенных ее значений. Форма обработанного сигнала представляет диагностическую информацию, например, анализ формы затухающих колебаний позволяет получить информацию, которая определяется частотой (периодом) собственных колебаний, скоростью их затухания и направлением, в котором производится удар и измеряется вибрация. Несимметрия сигнала вибрации может, с одной стороны, появиться при различного рода ударах в объекте диагностики, а с другой — явиться следствием нелинейности и перегрузок в измерительных и анализирующих трактах.
В вибрационной диагностике задачи определения вида распределения p(x) обычно не ставятся. Это связано с тем, что закон распределения суммы нескольких составляющих стационарной вибрации, как правило, мало отличается от нормального, а вибрация любого оборудования практически всегда содержит несколько компонентов разной природы. Поэтому более важной задачей становится количественная оценка отличия реального распределения p(x) от нормального. Зачастую, такая оценка проводится по четырем основным параметрам распределения p(x): первому начальному моменту (среднему значению), второму, третьему и четвертому центральным моментам распределения .
Среднее значение сигнала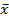 
определяется выражением
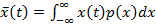(13.17)
Оценкой среднего значения функции x(t) называется величина, получаемая при усреднении по времени t значений x(t) на некотором интервале усреднения T
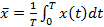(13.18)
В случае эргодического процесса истинное среднее значение получается переходом к пределу при устремлении T к бесконечности. Если 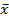рассчитывается по выборке из N значений сигнала x(t), то выборочная оценка среднего равна
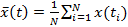(13.19)
В абсолютном большинстве случаев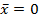 
.
Если значение 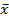отличается от нуля больше, чем на величину статистической ошибки, это чаще всего является признаком нелинейности каналов изменения и анализа сигнала вибрации.
Второй центральный момент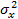 
распределения p(x) определяется выражением
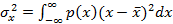(13.20)
Оценку среднего квадрата функции x(t) можно получить усреднением по времени значений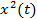 
на некотором интервале усреднения T:
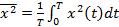(13.21)
В случае эргодического процесса истинный средний квадрат получается переходом к пределу при устремлении T к бесконечности.
При конечной выборке из N значений x(t) и условии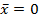
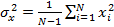(13.22)
Дисперсия 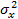— количественная оценка мощности переменных составляющих сигнала вибрации, но при анализе сигналов вибрации вместо дисперсии чаще всего используется величина СКЗ сигнала 
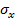. Среднеквадратичное значение есть положительный квадратный корень из среднего квадрата.
Среднеквадратическое отклонение есть положительный квадратный корень из дисперсии. При нулевом среднем значении оно равно среднеквадратичному значению.
Центральные моменты распределения порядка двух и выше обычно используются для количественных оценок отклонений от нормального закона распределения p(x) не всего сигнала вибрации, а предварительно выделенных из него компонентов, например, высокочастотных. При этом мера отклонения — нормированные (т. е. отнесенные соответственно к
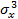и 
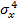) третий и четвертый моменты, которые называются коэффициентами асимметрии и эксцесса соответственно:
(13.23)
(13.24)
Коэффициент асимметрии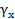 
выборочных значений вибрации обычно близок к нулю, если обеспечена линейность средств измерения вибрации, так как он оценивает асимметрию распределения p(x) относительно среднего (нулевого) значения.
Коэффициент эксцесса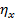 
характеризует степень отклонения формы закона распределения p(x) от нормального с тем же СКЗ 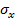. Сильнее всего он реагирует на появление выбросов в сигнале из-за возникновения микро- и макроударов в объектах контроля. Распределение, в отличие от нормального, становится островершинным с «хвостами» в области больших по модулю значений x(t).
Так как реализацию случайного процесса нельзя задать явной математической формулой, то для анализа случайных данных должны использоваться статистические методы. При этом важно уметь выявлять и учитывать статистические ошибки, связанные с оценками параметров и соотношениями между входными и выходными процессами преобразований.
Широкое распространение получили статистические методы анализа случайных вибросигналов, при которых определяются следующие характеристики измеряемого сигнала x (t):
— количественная оценка отличия реального распределения плотности вероятности от нормального распределения;
— пороговые значения для каждого из выбранных параметров вибрации, разделяющих объекты контроля на классы с разными свойствами по результатам периодического контроля этих параметров;
— количественная оценка тенденций изменения тех или иных параметров вибрации во времени, т. е. строятся соответствующие тренды.
— статистические связи между разными компонентами одного и того же сигнала вибрации.
Для описания свойств случайных вибросигналов используют следующие статистические характеристики:
— средние значения и средние квадраты;
— плотности вероятности (проверки нормальности, выявления нелинейностей, анализа экстремальных значений);
— ковариационные функции (выявление периодичностей, выделение сигналов из шума, измерение запаздываний, локализацию источников помех);
— функции спектральной плотности (задание динамических данных для тестовых программ, идентификация источников энергии и шума, оптимальный линейный прогноз и фильтрация, определение структур систем по наблюдениям входных и выходных процессов, предсказание выходных процессов по входным процессам, идентификация входных процессов по выходным процессам);
Для реализаций, принадлежащих двум разным случайным стационарным процессам, важное значение имеют совместные статистические характеристики:
— совместные плотности вероятности;
— взаимные ковариационные функции;
— взаимные спектральные плотности;
— частотные характеристики;
— функции когерентности.
Для выявления связи (зависимости) значений стационарного случайного сигнала x(t) в разные моменты времени t используется автокорреляционная функция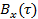 
вида
(13.25)
где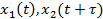 
— значения сигналов, измеренных в двух разных точках и в разные моменты времени.
Взаимная корреляционная функция стационарных случайных сигналов может быть представлена в виде
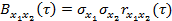(13.26)
где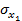 
, 
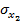— среднеквадратичные отклонения сигналов 
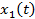и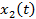 
; 
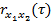— коэффициент взаимной корреляции, определяющий степень линейной зависимости двух случайных сигналов.
Взаимный корреляционный анализ сигналов чаще всего используется для выделения слабого сигнала на фоне сильных статистически не связанных помех, а также для определения пространственных координат их источника по величине временного сдвига Δτ. В отличие от автокорреляционного анализа он позволяет обнаружить не только узкополосные, но и коррелированные случайные широкополосные сигналы, поэтому более эффективно используется, например, для поиска утечек в трубопроводах по шумам, возникающим в зоне утечки и распространяющимся по потоку жидкости (газа).
Следует отметить, что в задачах обнаружения утечек чаще применяются не корреляционные, а спектральные методы анализа, так как взаимный спектральный анализ стационарных процессов дает больше информации. Но взаимный корреляционный анализ оказывается более эффективным при пространственном обнаружении нестационарных, в том числе импульсных, процессов и может использоваться, например, для обнаружения и определения координат источников акустической эмиссии в однородных нагруженных металлических конструкциях.
К числу важнейших характеристик относится спектральная плотность, которая пропорциональна средней мощности колебательного процесса, отнесенной к единице частотного диапазона при заданной частоте. Спектральная плотность случайного процесса, как неслучайная его оценка, является непрерывной функцией частоты.
Из частотных видов анализа вибрации наиболее широко используют спектральный, следящий и синхронный.
Спектральная плотность (иначе, спектр мощности) стационарной реализации интерпретируется как распределение среднего квадрата по частоте. Для оценивания спектра вычисляется средний квадрат в узкой полосе частот при разных центральных частотах, а затем полученное значение делится на ширину этой полосы. Общая площадь, лежащая под графиком спектральной плотности во всей полосе частот, равна суммарному среднему квадрату реализации.
Часть этой площади, заключенная между частотам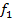и 
и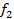 
, равна среднему квадрату, сосредоточенному в этой полосе частот.
Узкополосным называется случайный процесс, спектральная плотность которого существенно отлична от нуля лишь в пределах узкой полосы частот, сосредоточенной вблизи некоторой центральной частоты. Если мгновенные значения процесса имеют гауссовское распределение вероятностей, то его экстремальные значения приближенно подчиняются распределению Рэлея.
Если реализация стационарного случайного процесса s(t) задана на ограниченном интервале времени (0, T) и равна нулю вне его, то за оценку спектральной плотности мощности принимают величину
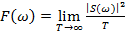(13.27)
которая дает усредненную картину распределения мощности по частоте. Здесь чертой отмечено усреднение по ансамблю реализаций.
В качестве диагностического признака вместо спектрального разложения процесса иногда используют интегральную характеристику:
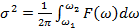(13.28)
в полосе частот (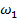 
, 
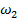), где изменения виброакустического сигнала проявляются наиболее заметно.
При диагностике объекта на каждом режиме работы полезно иметь таблицу основных частот возбуждения колебаний и их гармоник, с тем чтобы вести направленный поиск диагностических признаков. В ряде случаев в качестве диагностического признака может служить спектральная амплитуда на частоте возбуждения диагностируемого узла, если ее поведение однозначно связано с изменением соответствующего параметра состояния объекта. При наличии в спектре четко выраженного гармонического ряда или нескольких рядов частот, кратных основным частотам возбуждения объекта, удобно формировать диагностический признак из составляющих гармонического ряда, амплитуды гармоник которого несут информацию об изменении состояния узла объекта диагностирования. При этом наиболее простым и информативным признаком служит длина n-мерного вектора, компонентами которого являются амплитуды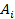 
гармонического ряда. В ряде случаев достаточно ограничиться числом ряда n = 5 . . . 10.
Для стационарных случайных сигналов можно использовать спектральное представление. Спектральный анализ вибрации позволяет разделить компоненты разной частоты, возбуждаемые разными источниками колебательных сил и имеющие разную природу и разные свойства. Чаще всего спектральные методы анализа вибрации используются для изучения вибрации машин и оборудования периодического действия. Физический спектральный анализ можно рассматривать как параллельную фильтрацию сигнала с помощью большого количества фильтров разной частоты и определение мощности его отдельных компонентов или их среднеквадратичного значения на выходе каждого из фильтров.
Случайный процесс характеризуется некоторым распределением его энергии по отдельным частотным составляющим. Такое распределение может быть описано некоторой функцией частоты, подобной по смыслу энергетическому спектру сигнала. Однако непосредственное применение аппарата преобразования Фурье к случайным процессам невозможно, из-за того что такое преобразование не существует по крайней мере для непрерывных случайных процессов ξ (t), так как не выполняется условие абсолютной интегрируемости
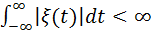(13.29)
В связи с этим рассматривается не полная энергия, а энергия за единицу времени.
Выделим отрезок реализации случайного вибросигнала, который представляет собой функцию времени в интервале [0, T]. Пусть для него существует преобразование Фурье
(13.30)
то применительно к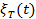 
и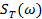 
можем записать равенство Парсеваля
(13.31)
Поделив левую и правую части этого равенства на длину интервала времени T, запишем:
(13.32)
Каждая часть этого равенства описывает среднюю мощность случайного вибропроцесса на интервале T.
При T →∞ в правой части равенства под знаком интеграла будет спектральная плотность мощности случайного вибропроцесса, которую будем обозначать F(ω). Тогда можно записать
(13.33)
Спектральная плотность мощности характеризует распределение мощности случайного процесса по частоте и определяется как аналитически, так и аппаратно.
Функцией корреляции случайных процессов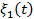 
и 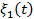называется смешанный центральный момент второго порядка этих процессов, взятых в различные моменты времен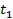и 
и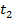 
. Для эргодических процессов она равна временному среднему от произведения двух реализаци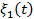й и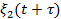 
и зависит от разности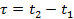 
(13.34)
В этом случае она называется функцией взаимной корреляции, в отличие от функции автокорреляции, которая получается при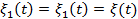 
:
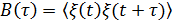(13.35)
Лекция № 14. Вибродиагностика. Часть третья
Дата: 2018-11-18, просмотров: 733.
