Вибродиагностика основана на измерении и исследовании вибрации.
Виброперемещение в большинстве технических задач (размах или амплитуда) измеряется в микрометрах (мкм), реже в метрах (м), миллиметрах (мм) или ангстремах (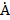 
). В англоязычных странах виброперемещение измеряют в миллидюймах (1/1000 дюйма; 1 дюйм = 2,54 см) и по традиции применяют значение размаха (peak-to-peak). В европейских странах принята международная система единиц, и виброперемещение измеряют в микрометрах (мкм).
Виброскорость (среднеквадратическое значение) измеряется в мм/с, м/с. В англоязычных странах — дюйм/с (ips). При измерении виброскорости используется как СКЗ, так и пиковые значения. В некоторых странах (например, США) более употребительным является пиковое значение.
Виброускорение (пиковое значение) измеряется в м/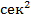 
или долях g = 9,81 
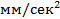. В англоязычных странах — 
.
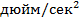Так как сила, действующая на массу, вызывает ее ускорение в направлении своего действия, а скорость и величина перемещения зависят от времени действия силы в данном направлении, то с увеличением частоты f период действия силы уменьшается, соответственно уменьшается виброскорость и, тем более, виброперемещение. Исходя из этого виброускорение целесообразно измерять на высоких частотах, так как его амплитуда пропорциональна квадрату угловой частоты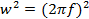 
.
Частоту вибрации измеряют в герцах (Гц) (1/с) или числах оборотов в минуту (об/мин) — для роторных машин.
В ряде областей техники результаты измерения виброускорения представляют в децибелах относительно выбранного условного нулевого значения уровня ускорения, например,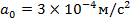 
, и определяют по формуле
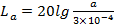(12.14)
где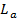 
- уровень ускорения, дБ; а – ускорение, 
.
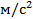Перевод скорости в децибелы относительно условного нулевого значения
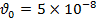м/с осуществляется по формуле
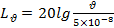(12.15)
где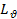 
- уровень виброскорости, дБ; ϑ – скорость, 
.
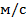Перевод виброперемещения в децибелы относительного условного нулевого уровня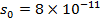 
мм осуществляют по формуле
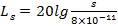(12.16)
где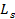 
- уровень виброперемещения, дБ; s – величина перемещения, 
.
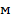Выражение результатов измерения виброперемещения в децибелах встречается достаточно редко.
В соответствии с ИСО-1683 используются следующие пороговые значения механических колебаний: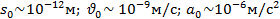 
Перечисленные пороговые величины приняты по ИСО-1683 таким образом, что числовые значения уровней виброперемещения, виброскорости и виброускорения механических колебаний с синусоидальной формой волны и угловой скоростью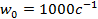 
равны друг другу.
Таким образом, абсолютные значения s, ϑ и a выражают в децибелах относительно их стандартного порогового значения. При сравнении значений механических колебаний достаточно показать лишь разность соответствующих уровней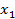 
и 
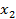в децибелах.
При выражении вибропараметров в линейных единицах измерений их размерность определяется масштабами соответствующих параметров. Для большинства машинных агрегатов амплитуда виброперемещений составляет величины порядка десятков микрон, а виброскорости — порядка десятков миллиметров в секунду. Поэтому при выражении вибропараметров в линейных единицах виброперемещение принято измерять в микронах (мкм), виброскорость — в мм/с, а виброускорение — в .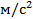
Классификация вибросигналов
В общем случае вибросигналы классифицируются на несколько видов:
— стационарные: случайные, детерминированные (периодические, квазипериодические);
— нестационарные: непрерывные, переходные.
Различным типам сигналов соответствуют различные типы спектров. Стационарные сигналы имеют постоянные по времени статистические параметры. Специальный класс стационарных сигналов представляют собой детерминированные сигналы, которые сохраняют постоянный частотный и амплитудный состав в течение длительного периода времени. Они подразделяются в свою очередь на периодические и квазипериодические. Реализация периодического сигнала непрерывно повторяется через равные отрезки времени.
Частота повторения квазипериодического сигнала незначительно варьируется по времени. Периодические вибросигналы имеют спектр с дискретными частотными компонентами. Случайные сигналы непредсказуемы по своему частотному составу и уровням амплитуды, однако их статистические характеристики постоянны.
Примером стационарной вибрации являются вибрации на частоте вращения энергетических турбоагрегатов. При этом гармоники и субгармоники вибрации представляют собой диагностический параметр для большинства опасных дефектов. Аномальная стационарная (практически неизменная во времени и малозависимая от режима) вибрация возникает после ремонта, монтажа, иногда и после очередного останова нагрузочного агрегата. Причинами стационарной повышенной вибрации на частоте вращения являются:
— сосредоточенный либо распределенный дисбаланс;
— остаточный прогиб одного из роторов;
— дефекты сопряжения роторов в муфтах;
— пониженная жесткость опорной системы (резонансные явления, отрывы и зазоры по корпусам и плитам, повреждения фундамента);
— расцентровка роторов по муфтам, повреждения уплотнений в турбопитательных насосах.
Нестационарные вибросигналы — сигналы, у которых амплитудные и частотные параметры меняются со временем. Непрерывный нестационарный сигнал — сигнал, который регистрируется постоянно, вне зависимости от длительности записи. Переходной вибросигнал — сигнал, начинающийся и заканчивающийся на нулевом уровне и длящийся конечное время. Нестационарная вибрация характеризуется функцией ее изменения во времени: внезапное изменение, при изменении режима нагрузки, медленный или быстрый монотонный рост (тренд), повышенные переменные по знаку изменения на неустановившихся режимах.
Причинами нестационарной вибрации энергетических турбоагрегатов могут быть следующие процессы:
— тепловой дисбаланс разного происхождения;
— дефекты подвижных муфт;
— тепловая (режимная) расцентровка валов;
— электромагнитные возмущения;
— поломка деталей ротора;
— задевание ротора; развитие трещины в роторе; нарастание прогиба ротора вследствие ползучести;
— повышенные радиальные зазоры по насадным деталям;
— деградация соединений опорной системы;
— деградация поверхностей скольжения подвижных корпусов;
— магнитная асимметрия ротора синхронной электрической машины;
— ослабление посадки насадных деталей.
Периодические вибросигналы
Периодической вибрацией называют колебательный процесс, в котором значения колебательной величины повторяются через одинаковые промежутки времени T в той же последовательности. В этом случае
x (t) = x (t+mT) (12.17)
где m = . . .−2,−1, 0, +1, +2 . . .; T — период колебаний.
Величина f = 1/T называется частотой колебаний и измеряется числом колебаний в одну секунду (Гц). Число полных угловых колебаний за 2π единиц времени называется угловой частотой (рад/с): ω = 2πf.
Непрерывная последовательность, выражающая совокупность всех частот на промежутке от нижней граничной частоты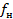 
до верхней граничной 
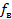называется частотным диапазоном. Ширина полосы частот, для которой 
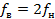, называется октавой. Диапазон имеет ширину k октав, если 
.
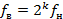Среди периодических вибросигналов наиболее простым видом вибрации (колебаний) являются гармонические колебания — периодическая вибрация с одной частотой. В этом случае колеблющаяся величина изменяется по косинусоидальному или синусоидальному законам, например, колебания вращающегося физического тела с неуравновешенным центром масс в вертикальном направлении (рис. 12.1).
Виброперемещение центра масс определится из выражения
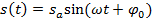, (12.18)
где s(t) — виброперемещение тела;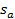 
— амплитуда виброперемещения; ω — угловая скорость колебаний; t — время; 
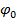— начальная фаза колебаний в исходном состоянии при t = 0; 
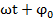— фаза колебаний.
Фаза колебаний ωt+ϕ0 определяет состояние колебательного процесса в заданный момент времени t. Периодом колебаний T называется наименьший промежуток времени, через который колеблющаяся система возвращается в исходное состояние. Фаза есть мера относительного сдвига во времени двух синусоидальных колебаний. Фазовый сдвиг — это разница в моментах начала отсчета между двумя и более колебательными процессами. Синфазными называют колебания, у которых сдвиг фаз равен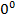 
, 
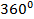,. Противофазными называют колебания, у которых сдвиг фаз равен 
.
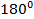Рис. 12.1. Простейшие гармонические колебания
Соответственно виброскорость ϑ и виброускорение a определяются по формулам
(12.19)
где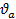 
и 
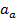— амплитуды соответственно виброскорости и виброускорения, 
, 
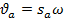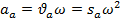. Из приведенных выражений следует, что виброскорость относительно виброперемещения имеет опережение фазы на 
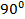, виброускорение — на ,.
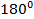Широкополосный установившийся вибрационный сигнал реальных машин имеет сложный характер и состоит из ряда гармонических составляющих (гармоник). Каждая из этих составляющих определяется ее частотой, амплитудой и фазой относительно некоторого известного начала отсчета.
Вибрации, которые могут быть представлены в виде суммы двух и более гармонических колебаний с разной частотой, называются полигармоническими (вибрации со многими частотами), например:
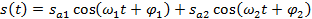(12.20)
где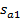 
, 
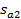— амплитуды виброперемещений гармонических составляющих соответственно с угловыми частотами 
, 
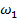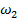и начальными фазам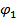и 
и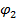 
.
Полигармоническая вибрация имеет место при воздействии на одну и тeже систему различных независимых гармонических колебаний в общем случае с различными амплитудами и начальными фазовыми углами. Для описания полигармонического процесса по заданным гармоническим составляющим нужно произвести сложение колебаний. Сложение гармонических составляющих вибрации, происходящих по одному направлению, называют скалярным.
На форму полигармонических вибраций большое влияние оказывает сдвиг начальных фаз между гармониками, вследствие чего процесс, содержащий гармоники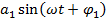 
, 
, 
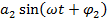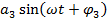при неизменных значениях амплитуд и частот гармоник при изменении начальных фазовых углов, существенно меняет свою форму.
Коэффициент формы для периодической вибрации — это отношение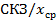 
.
Для гармонических колебаний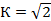 
, 
, 
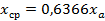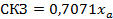, где 
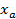— амплитуда гармонической вибрации.
Следует отметить, что среднеквадратичное значение периодической вибрации зависит от значений изменений фазовых углов гармоник, содержащихся в вибрационном процессе, в то время как изменение начальных фазовых углов гармоник полигармонической вибрации, приводящее к изменению его формы, сопровождается изменением пикового значения размаха и среднего значения вибрации.
При сложении колебаний с различными частотами можно отметить несколько характерных случаев:
1. Частоты слагаемых колебаний соотносятся как небольшие числа. В этом случае суммарное колебание имеет периодический характер, причем период является наименьшим кратным из периодов слагаемых колебаний, а формы весьма разнообразны.
2. Частота одного из слагаемых колебаний значительно превышает другую. В зависимости от того, амплитуда какого слагаемого колебаний (низкочастотного или высокочастотного) превалирует, форма колебаний близка либо к высокочастотным, либо к низкочастотным колебаниям.
3. Частота одного из слагаемых колебаний незначительно отличается от другого. В этом случае возникают биения. Участки суммарной кривой, на которой амплитуда биений максимальна, называются горбами, а участки, где амплитуда минимальна, — талиями. Расстояние между горбами или впадинами называется периодом биений, а обратная ему величина — число полных периодов изменения амплитуды в секунду — частотой биений, она равна разности частот слагаемых колебаний.
В практике вибрационных исследований встречаются задачи, когда интересующим результатом измерений является векторное сложение колебаний, измеренных в двух взаимно перпендикулярных направлениях.
При исследовании вибрационных сигналов широкое распространение получило спектральное представление, позволяющее свести анализ сложного сигнала к анализу его более простых составляющих. В общем случае спектральное представление сложных полигармонических колебаний получают, используя разложение сигнала в ряд Фурье.
Спектральный анализ используется для разделения сигналов на простейшие составляющие в частотной области. Он эффективен прежде всего в тех случаях, когда сигналы имеют периодические компоненты.
Периодический сигнал x(t) с периодом T и частотой повторения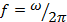 
имеет бесконечный спектр, который можно выразить в виде ряда Фурье
(12.21)
Где
, 
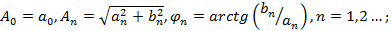
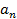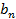– коэффициенты ряда Фурье, определенные по следующим выражениям:
(12.22)
Тригонометрический ряд Фурье описывает разложение сигнала на гармонические составляющие, позволяет проводить анализ сигналов в частотной области. Анализ с его использованием называется гармоническим. При таком представлении сигнала совокупность амплитуд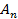 
называется амплитудным спектром, а совокупность фаз 
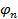— фазовым спектром.
Энергия сигнала x (t) за интервал времени [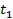 
, 
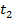] определяется выражением
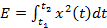(12.23)
Вводя преобразование Фурье,
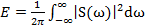(12.24)
Представление сигнала в виде тригонометрического ряда Фурье позволяет получить следующее выражение для энергии сигнала:
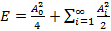(12.25)
Степень взаимозависимости двух сигналов 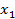, 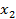в общем случае описывается корреляционной функцией:
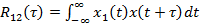(12.26)
где τ — смещение во времени одного сигнала относительно другого.
Корреляционная функция может также характеризовать взаимную зависимость двух значений одного сигнала x (t), разнесенных во времени
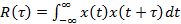(12.27)
В этом случае она называется автокорреляционной функцией.
При τ = 0 R(0) = E (т. е. автокорреляционная функция равна энергии сигнала).
Средняя мощность сигнала [ 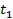, 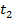] определится выражением
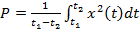(12.28)
Средняя мощность двух сигналов за интервал времени [ 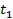, 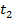] равна
(12.29)
где
(12.30)
— взаимная мощность.
Для периодического сигнала, имеющего период, равный T, средняя мощность определяется выражением
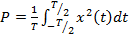(12.31)
Автокорреляционная функция
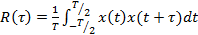(12.32)
Спектр называется линейчатым, если представляемые им гармонические составляющие обладают частотами с дискретными значениями и могут быть представлены в виде ряда Фурье, в отличие от сплошного спектра, обладающего непрерывной последовательностью частот, представляемых преобразованием Фурье. Спектральный анализ с использованием преобразования Фурье получил широкое распространение для анализа непериодических сигналов. Спектральный анализ эквивалентен преобразованию сигнала из временной области в частотную область и осуществляется с использованием прямого преобразования Фурье. Для обратного перехода используют обратное преобразование. Прямое и обратное интегральные преобразования Фурье для сигнала x (t) определяются следующим образом:
(12.33)
где ω— круговая частота; i — мнимая единица; S (ω) — спектральная плотность сигнала.
Лекция № 13. Вибродиагностика. Часть вторая
Дата: 2018-11-18, просмотров: 1606.
