Итак, для проверки статистических гипотез нам необходимо:

1. Сформулировать нулевую и альтернативную гипотезу.

2. Выбрать значение уровня значимости α.

3. Выбрать тот способ проверки, который будет использоваться.

Чтобы понять, что происходит дальше, рассмотрим пример.

Мы уже имели дело с нормальным распределением, полученным на основе исследования «Молодежь и наркотики». Для этого распределения среднее возраста равно 16,5 лет, стандартное отклонение — 1,5 года.

 Предположим, что для проверки ситуации с употреблением наркотиков среди девушек из участников исследования случайным образом была сформи­рована выборка объемом в 100 девушек. После проверки оказалось, что их средний возраст — 16,0 лет. Можно ли утверждать, что среднее значение воз­раста принявших участие в исследовании девушек (16,0 лет), меньше обще­группового показателя (16,5 лет)?

Сформулируем нулевую и альтернативную гипотезы:

Н₀ : Средний возраст девушек, принимавших участие в исследовании, не отличается от среднего возраста для всей совокупности испытуемых.

Н₁: Средний возраст девушек, принимавших участие в исследовании, мень­ше среднего возраста для всей совокупности испытуемых.

Выберем уровень значимости α =0,05.

Приступим к проверке.

Предположим, что верна нулевая гипотеза и на самом деле средний возраст девушек не отличается от значения 16,5 лет.

Данное предположение означает:

Если из участников исследования раз за разом случайным образом форми­ровать состоящую из девушек выборку численностью 100 человек и раз за разом определять среднее значение их возраста, то получаемые каждый раз значения будут отличаться друг от друга (например, в одном случае среднее значение возраста будет равно 16,0 лет, в другом — 15,9 лет, в третьем — 16,3 лет и т. д.). В математической статистике доказывается, что:

· после многократного повторения этой процедуры все средние будут иметь нормальный закон распределения;

· среднее всех средних будет равно общегрупповому значению (то есть 16,5 лет);

· стандартное отклонение для этого среднего будет равно 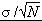, где σ — стандартное отклонение для всех результатов (в нашем случае σ = 1,5), N — объем извлекаемой выборки (у нас N= 100).

Для нового нормального распределения с 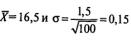 определим значение z для X_i=16,0: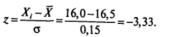      

По таблице 1 (Приложение 2) найдем вероятность того, что z сможет принять значение z ≤ -3,33 (или, что то же самое, площадь, отсекаемую от площади под кривой нормального распределения левее значения z = - 3,33)¹¹: р = 0,0005.

¹¹ На самом деле из таблицы мы находим площадь, лежащую правее значения z =3,33, но, поскольку кривая нормального распределения симметрична, это то же самое, что найти площадь левее z = -3,33.

Вернемся к нулевой гипотезе, которую мы проверяли. Мы предположили, что значение среднего возраста (16,0 лет), которое было получено для девушек, носит случайный характер и на самом деле их средний возраст не отличается от значения 16,5 лет. Однако вероятность случайного получения такого резуль­тата ничтожно мала (р =0,0005).

Поскольку столь маловероятное событие все же произошло, есть все осно­вания посчитать его неслучайным и тем самым отвергнуть нулевую гипотезу. Если мы это сделаем и примем альтернативную гипотезу, говорящую о неслу­чайном характере полученного результата, то такое решение будет ошибочным в 5 случаях из 10000 (р=0,0005). Это гораздо меньше того числа ошибок, кото­рые мы были готовы себе позволить (α=0,05, или 5 случаев из 100). Мы имеем полное право отвергнуть нулевую гипотезу и принять альтернативную.

Рассмотрим иную ситуацию.

Исследователь, воодушевленный полученным выше результатом, решил облегчить себе жизнь и для очередного изучения ситуации среди девушек сформировал выборку в 20 человек. Для этой выборки он вновь получил сред­нее значение возраста 16 лет. Может ли он сейчас сделать тот же самый вывод о том, что средний возраст девушек, принимавших участие в исследовании, меньше среднего возраста для всей совокупности испытуемых?

Повторим прежнюю последовательность действий и вычислим значение z для N=20 (помним, что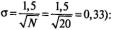

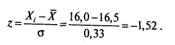
Из таблицы 1 (Приложение 2) найдем вероятность, соответствующую по­лученному значению

z : р =0,0643.

Если мы вновь отвергнем нулевую гипотезу, то это решение будет ошибоч­ным в более чем шести случаях из ста. Но максимальное число ошибок, кото­рые мы можем себе позволить, это 5 случаев из 100. Следовательно, у нас нет оснований отвергнуть нулевую гипотезу. Мы должны признать, что в данном случае средний возраст принимавших уча­стие в исследовании девушек не отличается от значения среднего возраста для всей со­вокупности испытуемых.

Из приведенных примеров следует один очень важный вывод: результат проверки статистических гипотез в значительной сте­пени зависит от размера выборки. Если ис­следователь изучает какую-либо ситуацию, то чем с большей по размеру выборкой он будет иметь дело, тем более достоверные ре­зультаты получит¹².

¹² В этом одна из проблем проверки статистических гипотез на основе свойств нормального распределения. Во многих случаях нет возможности получить большую по объему выборку. Психолог, работающий с аутичными детьми, социальный работник, исследующий случаи суицидов среди подростков, врач, изучающий очень редкое генетическое заболевание, — во всех этих случаях вряд ли можно рассчитывать на выборки численностью в сотни человек. Данное обстоя­тельство стало одним из толчков к развитию непараметрических методов статистики.

Как правило, проверка статистических гипотез связана с четким алгоритмом действий.

Вначале, в зависимости от характера решаемой задачи (что конкретно мы проверяем или сравниваем — средние значения, дисперсии, корреляции и др.), определяется способ проверки, формулируются нулевая и альтернативная гипотезы и выбирается значение уровня значимости α.

Затем, на основе имеющихся данных, вычисляется определенное эмпири­ческое значение К_эмпир (процедура вычисления К_эмпир определяется характером решаемой задачи и выбранным способом проверки).

Дальнейшие действия могут идти двумя путями.

Первый путь связан с определением вероятности р получения эмпириче­ского значения К_эмпир. Если эта вероятность окажется меньше или равна вы­бранному значению уровня значимости α, нулевая гипотеза отвергается и принимается альтернативная. Если вероятность р оказывается больше выбран­ного значения уровня значимости α, у нас нет оснований, чтобы отвергнуть нулевую гипотезу.

Во втором случае решается другая задача. Определяются значения К_критич для фиксированных вероятностей ошибки первого рода, используемых при проверке статистических гипотез (в большинстве случаев это р=0,05, р =0,01, р =0,001). Значение К_критич служит границей между той областью, где нулевая гипотеза принимается, и той областью, где нулевая гипотеза отвергается. Область, где нулевая гипотеза отвергается, в статистике называется критической областью. При использовании этого понятия необходимо учитывать ряд под­водных камней, с ним связанных.

Вернемся к примеру с покупкой обуви. Мы рассматривали три варианта альтернативной гипотезы (обувь на правую ногу больше обуви на левую ногу; обувь на правую ногу меньше обуви на левую ногу; обувь на правую ногу не равна обуви на левую ногу).

На языке статистики это означает необходимость использования правосто­ронней критической области, левосторонней критической области и двусто­ронней критической области. В качестве критических областей выступают «хвосты» нормального распределения, соответствующие вероятностям р=0,05, р=0,01 и р=0,001¹³ и расположенные слева или справа от медианы. Если ве­роятность, соответствующая значению К_эмпир, попадает вовнутрь критической области, то нулевая гипотеза отвергается.

¹³ Легко показать (см. табл. 1, Приложение 2), что этим вероятностям соответствуют значения z=±1,64, z =+2,32 и z =±3,08.

При использовании двусторонней критической области применяются оба «хвоста» нормального распределения. Происходит объединение двух предыду­щих вариантов альтернативной гипотезы: вначале проверяется предположение, что обувь на правую ногу больше обуви на левую ногу, а затем предположение, что обувь на правую ногу меньше обуви на левую ногу.

Что при этом происходит с вероятностью ошибки первого рода р (или уров­нем значимости α)? Эта вероятность удваивается (суммируется площадь двух «хвостов») и может выйти за пределы допустимых рамок. Например, если пер­вые две гипотезы проверялись для уровня значимости        α =0,05, то третья будет проверена для уровня значимости α =0,05+ 0,05 = 0,1. Но это значение прак­тически не применяется в математической статистике при проверке гипотез.

Чтобы уровень значимости α при использовании двусторонней критической области¹⁴ не выходил, например, за рамки α = 0,05, необходимо, чтобы провер­ка гипотез для односторонней критической области происходила на уровне не большем чем α /2 = 0,025.

¹⁴ Ее признаком обычно является знак неравенства в записи альтернативной гипотезы: Χ≠Υ.

Иными словами, если, например, на уровне значимости α =0,05 проверя­ется гипотеза Н₀: Χ≠Υ, при альтернативной гипотезе Н₁: Χ≠Υ, то это означает объединение двух односторонних критических областей (правосторонней и левосторонней), соответствующих уровням значимости α /2 = 0,025. Поэтому проверка гипотез при применении двусторонней критической области носит более строгий характер. Если по результатам такой проверки нулевая гипотеза отвергается, то она тем более отвергается при использовании односторонней критической области (право- или левосторонней).

При проверке гипотез иногда бывают ситуации, когда при применении двусторонней критической области нет оснований отвергнуть нулевую гипо­тезу, а при использовании односторонней — есть. Например, при использо­вании двусторонней критической области выяснилось, что граница, отделяю­щая область принятия нулевой гипотезы от области, где она отвергается (критическая область), соответствует р=0,08. Это превышает верхний предел уровня значимости α =0,05, и нулевая гипотеза не отвергается. Но значение р=0,08 образовалось путем сложения площадей двух «хвостов» слева и справа, по 0,04 каждая. Поэтому если мы соответствующим образом сформулируем альтернативную гипотезу и перейдем к использованию односторонней кри­тической области, то будем иметь дело с площадью (вероятностью) только одного «хвоста», равной р =0,04. Это меньше чем α = 0,05, и нулевая гипотеза будет отвергнута.

Во многих статистических таблицах, используемых при проверке статисти­ческих гипотез, указывается, какой критической области (односторонней или двусторонней) соответствуют приводимые в ней значения. Важно ясно пред­ставлять, для какой из них (односторонней или двусторонней) производится проверка¹⁵. От этого зависят значение К_критич и, как следствие, результат про­верки.

¹⁵ Во многих случаях можно перейти от результата проверки для односторонней критической области к результату проверки для двусторонней критической области путем умножения значения а на два. Например, если нулевая гипотеза для односторонней критической области была отверг­нута для значения α =0,01, то это означает, что она будет также отвергнута и для двусторонней критической области на уровне α =0,02. Аналогичным образом в ряде случаев можно переходить от результата проверки для двусторонней критической области к результату проверки для одно­сторонней критической области путем деления значения α на два.

Во многих случаях значение К_критич, вычисленное для определенной веро­ятности ошибки первого рода р, зависит также от другого статистического показателя, называемого числом степеней свободы (обозначается как df — degrees of freedom).

Число степеней свободы df является важным показателем, определяющим наши возможности в варьировании экспериментальных данных без изменения полученных результатов.

Например, известно, что среднее арифметическое трех чисел а, b, с равно 4:

(a+b+с)/3=4

Очевидно, можно найти много чисел а, b, с, которые удовлетворяют этому условию (например, 7, 3, 2 или 15, -8, 5). Но обратите внимание на то, что фактически мы свободны в выборе только двух чисел из трех. Третье число предопределено выбором двух предыдущих. Если мы выбрали 6 и 5, то для получения среднего арифметического, равного 4, в качестве третьего числа мы можем использовать только число 1 . Другой возможности нет. Таким образом, для трех чисел мы имеем две степени свободы.

Аналогично, если вы складываете мозаику из 100 элементов, то только 99 из них «обладают свободой». Последний элемент должен встать на единствен­ное определенное ему место, не имея «свободы выбора».

В ряде случаев (но не всегда!) число степеней свободы определяется как (N - 1), где N — размер (объем) выборки. Например, для выборки N =35 (чис­ло подростков, опрошенных о возрасте начала курения) при проверке ряда гипотез число степеней свободы будет (35 — 1) = 34.

Для большинства случаев проверки статистических гипотез данные о К_критич, соответствующих значениях вероятности ошибки первого рода р, и числе сте­пеней свободы  df приводятся в специальных статистических таблицах. Это избавляет от необходимости дополнительных вычислений, поскольку про­цедура проверки превращается в выбор значения уровня значимости а и срав­нение вычисленного значения К_эмпир со значением К_критич, которое берется из соответствующей статистической таблицы для случая α = р¹⁶

¹⁶ Как можно видеть, судьба нулевой гипотезы начинает зависеть от значения α. У исследова­теля появляется определенная возможность для маневра, связанная с варьированием этим зна­чением. Например, для выбранного значения α = 0,01 может оказаться, что К_эмпир < К_критич.Оснований отвергнуть нулевую гипотезу нет. Но если выбрать α =0,05, то ему будет соответство­вать другое значение К_критич и вполне возможно, что сейчас К_эмпир ≥ К_критич и нулевая гипотеза будет отвергнута.

В большинстве случаях (но не всегда!) здесь используется следующее пра­вило (рис. 1.25):

1. Если К_эмпир < К_критич, нет оснований отвергнуть нулевую гипотезу.

2. Если К_эмпир ≥ К_{критич,} нулевая гипотеза отвергается и принимается альтер­нативная.

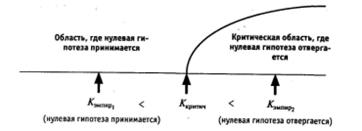
Рис. 1.25. Правило принятия решений при проверке статистических гипотез

(случай односторонней критической области)

Используемые способы проверки гипотез (тесты) в большинстве случаев носят имена своих создателей — тех исследователей (статистиков, математиков, экономистов, инженеров), которые впервые предложили тот или иной тест и рассчитали для него соответствующие статистические таблицы. В Приложении 1 приведены краткие сведения о тех людях, чьи имена носят популярные стати­стические тесты, рассмотренные в этой книге.