Проблема: Учет гендерных особенностей в процессе обучения и профессиональной деятельности
1) Проанализируйте содержащуюся в таблице 1 информацию об отличительных особенностях в способах мышления и деятельности девочек и мальчиков (материал подготовлен на основе статьи: Каплунович И.Я. О различиях в математическом мышлении мальчиков и девочек // Педагогика. – 2001. – № 10. – С. 30-35).
Таблица 1
Гендерные особенности в способах мышления и деятельности мальчиков и девочек
| Девочки | Мальчики |
| Различия в деятельности: | |
| Более последовательны в своих действиях, логичны, не чуждаются рутинной вычислительной работы, четко придерживаются алгоритмов, правил решения задачи и норм его оформления | Быстрее улавливают суть дела, любят искать и находить бытовые интерпретации для математических фактов и объектов, чаще генерируют идеи (хотя и не всегда верные) и не любят их проверять, т.е. ориентированы больше на процесс, чем на результат |
| Особенности в запоминании и работе с наглядностью: | |
| В памяти откладывается визуальный образ | Фиксируют взаимное расположение линий, поверхностей и их элементов |
| Легче создают синтетические образы (яркие, эмоциональные, адекватные реальным объектам) Например, любят рисовать красавиц и их наряды со всеми деталями | Легче создают конструктивные образы, отражающие не вещественный предмет, а его структуру, отношения между элементами в нем. Например, с удовольствием изображают технику (танки, машины), при этом для них важно не столько внешнее оформление картины, сколько четкая фиксация и закрепленность взаиморасположенных объектов |
| Различия в пространственной ориентации: | |
| Легче создают пространственные образы | Легче оперируют пространственными образами |
| Лучше ориентируются при наличии и выделении синтетических объектов, им присуще « чувство направления». При ориентации создают «карту-путь», т.е. прослеживают пройденный путь и при этом определяют местоположение относительно начальной и конечной точек | Лучше ориентируются среди конструктивных образов (строений в городах). При ориентации создают «карту-обозрение», т.е. создают целостную картину (своеобразную карту) всех пространственных отношений и объектов окрестности, взаиморасположения предметов или их элементов |
Указанные в таблице гендерные особенности оказывают влияние на развитие математического мышления учащихся, результаты освоения ими математики.
Приведите примеры из собственной жизненной практики, демонстрирующие влияние гендерных особенностей на результаты изучения тех или иных учебных предметов.
2) Психологи определяют разные причины отличительных особенностей в математическом мышлении девочек и мальчиков. Например, Р. Гэр объясняет различия в математическом мышлении учащихся тем, что у мужчин мозг на 10% больше, чем у женщин. Однако это не обеспечивает их общее интеллектуальное преимущество. Различия наблюдаются только в пространственной ориентации. Это связано с тем, что при относительном равенстве серой массы женский мозг уступает мужскому в количестве белого вещества, отвечающего за ориентацию.
Ученые Бергенского университета объясняют причину различий в математическом мышлении уровнем притязаний (самооценки) у учащихся (более высокой математической Я-концепцией у мальчиков по сравнению с девочками). Оказывается, причина кроется в различном воспитании тех и других, что и сказывается на формировании умений самооценки.
Проанализировав представленные выше позиции ученых, определите систему дисциплинарно-учебных требований к ребенку в семье с учетом гендерных особенностей.
3) Проанализируйте следующий подход к объяснению причин гендерных различий в мышлении женщин и мужчин:
Структура математического мышления, по данным психологических исследований включает в себя 5 основных пересекающихся подструктур, среди которых всегда существует главная – доминантная. Поясним это на задачах.
Укажите среди приведенных ниже фигур лишнюю или лишние:
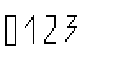
Возможны различные варианты ответов, по которым можно судить о доминантной подструктуре математического мышления:
0, т.к. эта цифра единственная, которая представляется в виде замкнутой ломаной;
1 и 2, т.к. они не похожи на буквы;
1, т.к. в начертании нет параллельных отрезков;
1, т.к. цифра состоит из двух, а не четырех отрезков, как остальные;
1, т.к. остальные можно преобразовать друг в друга (перекомбинировать).
Каждый из ответов имеет право на существование. Дело в том, что при изучении различных математических объектов человек вычленяет в них, прежде всего, отношения в зависимости от преобладающей подструктуры своего математического мышления (см. табл. 2).
С самого раннего детства девочек и мальчиков воспитывают по-разному, а потому формируют у них разные интересы, потребности и особенности мышления. От девочек в первую очередь требуют аккуратности и исполнительности. Вместе с тем считается, что самой мужской природе эти качества противоречат. Мальчишки по природе – бунтари, от них ждут неожиданностей, избирательности, неординарности.
По результатам проведенного И.Я. Каплуновичем исследования можно утверждать, что у девочек формируются, прежде всего, топологическая, метрическая и порядковая подструктуры. У мальчиков развивается и преобладает конструктивное мышление (разбирают и собирают машинки, играют с конструктором). Таким образом, в дальнейшем у них будут преобладать алгебраическая и проективная подструктуры (см. табл. 2).
Таблица 2
Подструктуры математического мышления
|
Подструктуры | ||||
| топологическая | проективная | порядковая | метрическая | алгебраическая |
| У людей, кто выбрал первый вариант ответа, развита топологическая подструктура. Это проявляется в том, что они вычленяют в объектах и легче оперируют такими пространственно-математическими характеристика-ми, как «непрерывно-разрывно», «связно-несвязно», «компактно-некомпактно», «принадлежит-не принадлежит», «внутри–снаружи». Они не любят торопиться. Каждое действие осуществляют очень подробно, стараясь не пропустить в нем ни одного звена. И в данном задании «топологи» вычленили свойство замкнутости в начертании фигуры. | Тем, у кого преобладает проективная подструктура, ближе второй ответ. Любимое занятие для них – рассматривать объект с различных точек зрения, под разным углом, устанавливать соответствие между объектом и его изображением и наоборот, искать и находить возможности использования объекта в практике, его бытовое назначение и применение. Поэтому, рассматривая заданное изображение предмета, они увидели, что некоторые цифры похожи на буквы, а другие – нет. | Сравнивать и оценивать в общем качественном виде: «равно-неравно», «больше-меньше», «выше-ниже», «над-под» – свойственно тем, у кого доминантная подструктура – порядковая. Вместе с тем им очень важна форма объектов, их соотношение (именно поэтому они выбирают третий из предложенных ответов), направление движения (по или против часовой стрелки, вверх или вниз). Действуют эти люди логично, по порядку. Работа по алгоритму для них – любимое занятие. | «Метристы» – люди с главной метрической подструктурой – акцентируют свое внимание на количественных характеристиках. Основной вопрос для них – «сколько?» (какова длина, площадь, расстояние, величина в числовом выражении). Поэтому именно они выделили в задании количество отрезков в начертании каждой из цифр (четвертый вариант). | Люди с алгебраической доминантной подструктурой (композиционной) выбирают пятый вариант ответа. Они постоянно стремятся к всевозможным комбинациям, |
| манипуляциям, вычленению частей и сбору их в единое целое, к сокращению и замене нескольких преобразований одним. Это те самые «торопыги», которые в противоположность «топологам» не хотят и с огромным трудом заставляют себя подробно прослеживать, записывать, объяснять все шаги решения или обосновывать собственные действия. Эти «великие комбинаторы» думают и делают быстро, но при этом часто и ошибаются. | ||||
Таблица 3
Сравнительная характеристика особенностей мышления мальчиков и девочек
| Девочки | Мальчики |
| Успешнее в оформлении работы, анализе задачи, последовательности собственных действий и их обосновании | Успешнее в генерировании идей и выдвижении гипотез |
| Тяготение к «внутренней геометрии», что объясняется играми в дошкольном возрасте («дом», «классики»), требующими ограниченного замкнутого пространства. Пространственные манипуляции с этими локальными, рядом расположенными объектами не требуют (иногда даже запрещают) выхода в неограниченное пространство, мир внешней геометрии | Тяготение к «внешней геометрии» связано с тем, что преобладающие игры (катание машины по длинным разнообразным дорогам, игра в конструктор или войну), которые предполагают постоянные перемещения, требуют неограниченного пространства. |
| Как результат: | |
| Успешнее в решении геометрических задач, требующих анализа и оперирования в рамках одной ограниченной и замкнутой геометрической фигуры. Лучше могут решить задачу о том, как расставить мебель в комнате, как тот или иной предмет одежды будет выглядеть на человеке | Предпочитают геометрические преобразования (осуществление поворотов, проецирование), вычленяют элементы и манипулируют несколькими фигурами на плоскости или в пространстве. Лучшая ориентация в окружающем незамкнутом пространстве (например, более уверенное управление транспортным средством) |
Проанализировав представленный материал, ответьте на следующие вопросы:
а) Можно ли утверждать, что алгебраическая и проективная подструктуры более весомы для математической и др. видов естественно-научной деятельности, чем те, которые обычно развиваются у девочек (топологическая, метрическая, порядковая)?
б) Согласны ли Вы с мнением, что снижению успеваемости у девочек по математике по сравнению с мальчиками способствуют учителя-женщины? Обоснуйте ответ, проанализировав следующее доказательство:
Учительницы строят свои объяснения с явной опорой на топологические, порядковые и метрические подструктуры, наиболее развитые у них самих. Такие объяснения более понятны девочкам, поэтому на первых порах девочки быстрее «схватывают» и усваивают материал, часто опережая мальчиков. Учащимся предъявляются «женские» требования, а именно: высокое качество оформления работы, обязательное доведение решения до числового ответа, соблюдение жесткой последовательности в решении, обязательная проверка решения. Для мальчиков такие требования являются сложными для выполнения, а девочкам данная работа дается легко. Однако в старших классах и, особенно, в вузе, где преподавателей-мужчин больше, многие формальные требования снижаются. Тогда наступает «звездный час» юношей, а девушки начинают замечать свое «отставание» (хотя не столько отстают девушки, как более быстро развиваются математические способности юношей).
Как Вы думаете, может ли снижаться интерес к математике у мальчиков в силу применения учителями «женских требований»?
в) Как можно стимулировать развитие алгебраической и проективной подструктур мышления у девочек?
г) Целесообразно ли снижение требований по оформлению решения задач по отношению к мальчикам и по решению задач на генерацию идей по отношению к девочкам?
д) Нужно ли создавать отдельные классы для мальчиков и для девочек или, наоборот, целесообразнее создавать смешанные группы и включать мальчиков и девочек в совместную учебную деятельность?
е) Какое мышление «мужское» или «женское» лучше для Вашей будущей профессиональной деятельности? Согласны ли Вы с утверждением, что ни одно из представленных типов мышления не лучше и не хуже – они просто разные и дополняют друг друга?
4) Какие гендерные особенности детей надо учитывать в семейном воспитании? Определите наиболее эффективные пути и способы умственного развития девочек и мальчиков в семье с учетом их гендерных особенностей.
5) При организации учебных занятий с персоналом или разрешении воспитательных проблем в процессе профессиональной деятельности надо ли учитывать гендерные различия сотрудников? Если надо, то – какие и каким образом? Поясните на примерах из сферы будущей профессии.
Дата: 2018-12-21, просмотров: 424.