Под иррациональным неравенством понимают неравенство, в котором неизвестные величины находятся под знаком корня.
Способ решения таких неравенств состоит в преобразовании их к рациональным неравенствам путем возведения обеих частей неравенства в степень.
Решение иррациональных неравенств осложняется тем обстоятельством, что здесь исключена возможность проверки, в связи с этим необходимо стараться делать все преобразования равносильными.
При решении иррациональных неравенств нужно запомнить правило:
при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству;
если обе части неравенства возводят в чётную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
Но если при решении уравнений в результате возведения четную степень мы могли получить посторонние корни (которые, как правило легко проверить) и не могли потерять корни, то корни неравенства при бездумном возведении в четную степень могут одновременно и теряться, и приобретаться.
Иррациональное неравенство 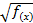 < g(х)
< g(х)  или
или 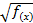 ≤ g(х)
≤ g(х)  равносильно системе неравенств:
равносильно системе неравенств:
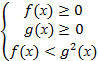 или
или 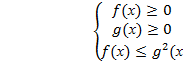
Иррациональное неравенство 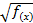 > g(х)
> g(х)  или
или 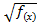 ≥ g(х)
≥ g(х)  равносильно совокупности двух систем неравенств:
равносильно совокупности двух систем неравенств:
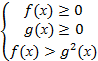
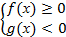 или
или 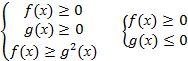
В связи с этим основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств.
Пример 1. Решить неравенство 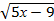
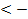 4.
4.
Решение. Заметим, что правая часто этого неравенства отрицательна, в то время как левая часть неотрицательна при всех значениях x, при котоҏыҳ она определена. В связи с этим неравенство решений не имеет.
Ответ. Решений нет.
Пример 2. Решить неравенство 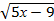
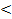 4.
4.
Решение. Область определения данного неравенства 5х-9≥0, х≥9/5.
Обе части неравенства неотрицательны, возведем их в квадрат: 5х-9< 16, х< 5.
Найдем пересечение полученного множества решений с областью определения неравенства, получим 9/5≤х<5.
Ответ : 9/5≤х<5
Пример 3. Решить неравенство 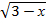 ≥ 7.
≥ 7.
Решение. Область определения данного неравенства 3-х ≥0, х≤3.
Обе части неравенства неотрицательны, возведем их в квадрат: 3-х≥ 49, -х ≥ 46, х ≤ -46.
Найдем пересечение полученного множества решений с областью определения неравенства, т.е. решение системы: 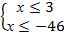 . Имеем два неравенства с одинаковым знаком, вспомним: «меньше меньшего», итак
. Имеем два неравенства с одинаковым знаком, вспомним: «меньше меньшего», итак 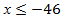 .
.
Ответ: 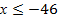 .
.
Пример 4. Решить неравенство  < 3х.
< 3х.
Решение. Данное неравенство равносильно системе неравенств: 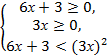
Найдем решения каждого из неравенств:
1) 6х + 3 ≥0, х≥-0,5.
2) 3х ≥ 0, х≥0.
3) 6х+3< (3х)2, -9х2+6х+3<0, 3х2-2х-1>0, решаем квадратное уравнение, находим х1=1, х2=-1/3. Применим метод интервалов: х< -1/3, х>1.
Запишем решения системы: 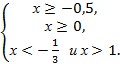 Получаем х>1.
Получаем х>1.
Ответ: х>1.
Задание для групповой и самостоятельной работы.
Решить неравенства.
1. 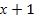 > х-1,
> х-1,
2. 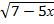 >3,
>3,
3. 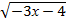 < 1,
< 1,
4. 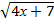 ≤ 5,
≤ 5,
5. 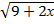 ≤ 4,
≤ 4,
6. 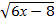 ≤ -6,
≤ -6,
7. 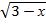 > х-1,
> х-1,
8. 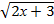 < х,
< х,
9. 5 + 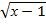 ≤ 3,
≤ 3,
10. 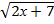 - 2≥ х
- 2≥ х
11. 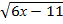 < х-1
< х-1
12. 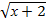 ≥6.
≥6.
Контрольные вопросы.
1. Что такое арифметический корень п-й степени?
2. Свойство корней?
3. Какие уравнения называются иррациональными?
4. Какие существуют способы решения иррациональных уравнений?
5. Почему при возведении в четную степень необходимо делать проверку?
6. Когда иррациональное уравнение не имеет решений?
7. Какие неравенства называются иррациональными?
8. Как решаются иррациональные неравенства?
Практическое занятие № 44
Выполнение заданий на решение логарифмических уравнений и неравенств
Цель работы:
- научиться решать простейшие логарифмические уравнения и неравенства.
Теоретическое обоснование
Логарифмические уравнения
Определение - Логарифмическим уравнением называется такое уравнение, в котором неизвестное содержится под знаком логарифма (в частности, в основании логарифма).
При решении таких уравнений обе части уравнения представляют в виде логарифмов с одинаковым основанием. У равных логарифмов с равными основаниями логарифмируемые выражения равны. После решения такого уравнения необходимо выполнить проверку.
Пример 1 - Решить уравнение 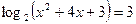 .
.
Решение.
По определению логарифма 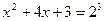 , то есть
, то есть 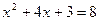 ,
,
или 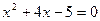 . Корнями данного квадратного уравнения являются числа -5 и 1. Следовательно, эти числа являются корнями логарифмического уравнения.
. Корнями данного квадратного уравнения являются числа -5 и 1. Следовательно, эти числа являются корнями логарифмического уравнения.
Ответ: -5; 1.
Пример 2 - Решить уравнение 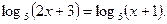
Решение.
Это уравнение определено для тех значений х, при которых выполнены неравенства 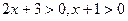 . Для этих х данное уравнение равносильно уравнению 2х +3 = х+1. Отсюда х = -2. Однако, число х = -2 не удовлетворяет неравенству х+1 > 0. Следовательно, данное уравнение корней не имеет.
. Для этих х данное уравнение равносильно уравнению 2х +3 = х+1. Отсюда х = -2. Однако, число х = -2 не удовлетворяет неравенству х+1 > 0. Следовательно, данное уравнение корней не имеет.
Пример 3 - Решить уравнение 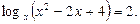
Решение.
Этому уравнению удовлетворяют все числа, больше 0, и отличные от 1, при условии, что справедливо равенство 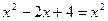 , то есть -2х + 4 = 0, откуда х = 2.
, то есть -2х + 4 = 0, откуда х = 2.
Ответ: 2.
Логарифмические неравенства
Решение логарифмических неравенств основано на свойстве логарифмической функции: функция возрастает, если основание больше 1, и убывает, если 0 < а < 1.
Пример 4 - Решим неравенство 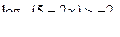 Решение.
Решение.
Число -2 равно 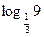 . Поэтому данное неравенство можно переписать в виде
. Поэтому данное неравенство можно переписать в виде
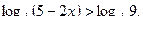 Логарифмическая функция с основанием
Логарифмическая функция с основанием 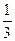 определена и убывает на множестве положительных чисел. Следовательно, второму неравенству удовлетворяют такие числа х, для которых выполняется условие
определена и убывает на множестве положительных чисел. Следовательно, второму неравенству удовлетворяют такие числа х, для которых выполняется условие
0 < 5-2x < 9, откуда -2 < x < 2,5.
Ответ: (-2; 2,5).
Практическая часть
Вариант 2 Вариант
Решить уравнение и неравенство: Решить уравнение и неравенство:
1) 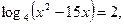 1)
1) 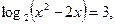
2) 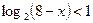 2)
2) 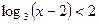
Вариант 4 Вариант
Решить уравнение и неравенство: Решить уравнение и неравенство:
1) 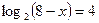 ; 1)
; 1) 
2) 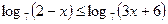 2)
2) 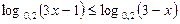
Вариант 6 Вариант
Решить уравнение и неравенство: Решить уравнение и неравенство:
1) 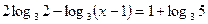 1)
1) 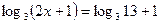
2) 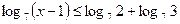 2)
2) 
Вариант 8 Вариант
Решить уравнение и неравенство: Решить уравнение и неравенство
1)  1)
1) 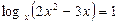
2) 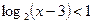
 2)
2) 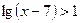
Вариант 10 Вариант
Решить уравнение и неравенство: Решить уравнение и неравенство
1) 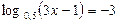 1)
1) 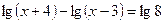
2) 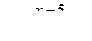 2)
2) 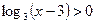
Контрольные вопросы
1 Понятие логарифмического уравнения.
2 Свойство логарифмической функции, на котором основано решение логарифмических неравенств.
3 Свойства логарифмов.
Практическое занятие № 45
Выполнение заданий на решение тригонометрических уравнений и неравенств
Вариант 1
Решите уравнение:
а) 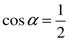 ;
;
б) 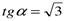 .
.
Решите уравнение:
а) 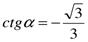 ;
;
б) 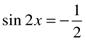 .
.
Решите уравнение:
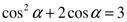 .
.
Решите неравенство:
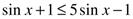
Решите уравнение:
а) 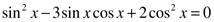 ;
;
б) 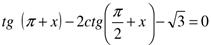 .
.
Решите уравнение:
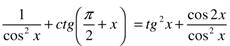
Вариант 2
Решите уравнение:
а) 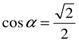 ; б)
; б) 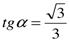 .
.
Решите уравнение:
а) 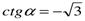 ; б)
; б) 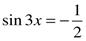 .
.
Решите уравнение:
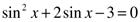 .
.
Решите неравенство:
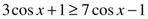
Решите уравнение:
а) 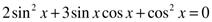 ;
;
б) 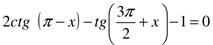 .
.
Решите уравнение:
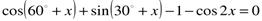
Дата: 2018-12-21, просмотров: 416.