1. loga a = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
2. loga 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
2. Логарифмическая функция.
Определение. Функцию, заданную формулой y =logax, называют логарифмической функцией с основанием а.
1. Область определения логарифмической функции — множество всех положительных чисел R+, т. е. D(loga)=R+.
2. Область значений логарифмической функции — множество всех действительных чисел.
3. Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).
Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1; loga 1 =0 при любом а>0, так как а0 = 1.
Вследствие возрастания функции при а>1 получаем, что при х>1 логарифмическая функция принимает положительные значения, а при 0<a<1—отрицательные.
Если 0<а<1, то y=logax убывает на R+, поэтому loga x>0 при 0<x<1 и logax<0 при х>1.
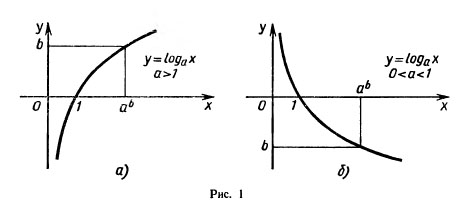
Опираясь на доказанные свойства, нетрудно построить график функции y = loga х при а>1 (рис. 1, а) и0<а<1 (рис. 1,б).
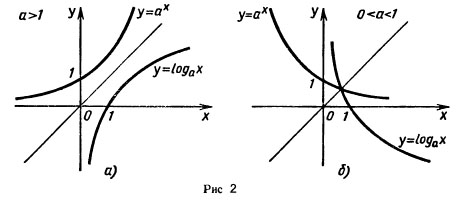
Справедливо следующее утверждение: Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х
Текст задания
1. Выполните действия:
| Свойства логарифмов Вариант 1 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 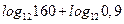
| 1) 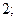 2) 2)  3) 3) 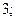 4) 4) 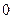
|
| А2 | Упростите: 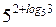
| 1) 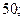 2) 2) 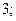 3) 3) 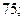 4) 4) 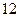
|
| А3 | Вычислите: 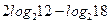
| 1) 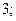 2) 2) 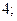 3) 3) 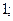 4) 4) 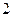
|
| А4 | Найдите значение выражения: 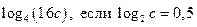
| 1) 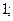 2) 2) 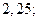 3) 3) 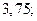 4) 4) 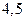
|
| А5 | Найдите значение выражения: 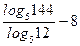
| 1) 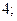 2) 2) 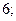 3) 3) 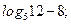 4) 4) 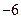
|
| А6 | Вычислите: 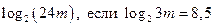
| 1) 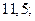 2) 2) 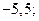 3) 3) 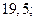 4) 4) 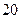
|
| А7 | Найдите значение выражения: 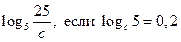
| 1) 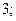 2) 2) 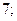 3) 3) 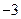 4) 4) 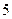
|
| А8 | Вычислите 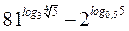
| 1) 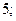 2) 2) 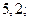 3) 3) 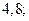 4) 4) 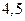
|
| Свойства логарифмов Вариант 2 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 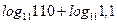
| 1)  2) 2) 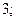 3) 3) 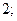 4) 4) 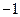
|
| А2 | Упростите: 
| 1) 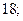 2) 2) 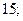 3) 3) 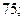 4) 4) 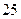
|
| А3 | Вычислите: 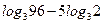
| 1) 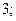 2) 2) 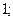 3) 3) 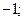 4) 4) 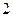
|
| А4 | Найдите значение выражения: 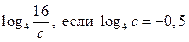
| 1) 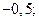 2) 2) 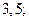 3) 3) 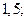 4) 4) 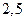
|
| А5 | Найдите значение выражения: 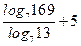
| 1) 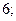 2) 2) 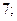 3) 3) 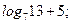 4) 4) 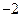
|
| А6 | Вычислите: 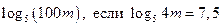
| 1) 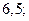 2) 2) 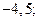 3) 3) 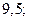 4) 4) 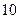
|
| А7 | Найдите значение выражения: 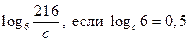
| 1) 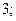 2) 2)  3) 3) 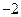 4) 4) 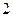
|
| А8 | Вычислите 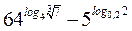
| 1) 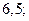 2) 2) 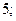 3) 3) 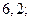 4) 4) 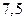
|
| Свойства логарифмов Вариант 3 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 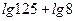
| 1) 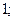 2) 2) 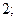 3) 3) 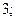 4) 4) 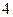
|
| А2 | Упростите: 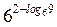
| 1) 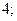 2) 2) 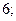 3) 3) 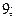 4) 4) 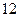
|
| А3 | Вычислите: 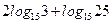
| 1) 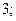 2) 2) 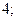 3) 3) 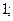 4) 4) 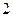
|
| А4 | Найдите значение выражения: 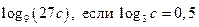
| 1) 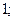 2) 2) 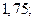 3) 3) 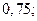 4) 4) 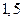
|
| А5 | Найдите значение выражения: 
| 1) 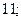 2) 2) 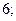 3) 3) 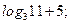 4) 4) 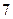
|
| А6 | Вычислите: 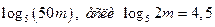
| 1) 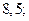 2) 2) 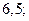 3) 3) 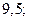 4) 4) 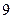
|
| А7 | Найдите значение выражения: 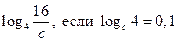
| 1) 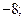 2) 2) 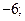 3) 3) 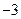 4) 4) 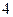
|
| А8 | Вычислите 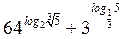
| 1) 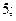 2) 2) 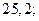 3) 3) 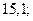 4) 4) 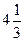
|
| Свойства логарифмов Вариант 4 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 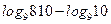
| 1)  2) 2) 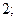 3) 3) 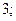 4) 4) 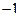
|
| А2 | Упростите: 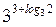
| 1) 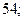 2) 2) 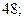 3) 3) 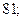 4) 4) 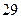
|
| А3 | Вычислите: 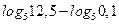
| 1) 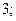 2) 2)  3) 3) 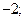 4) 4) 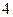
|
| А4 | Найдите значение выражения: 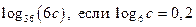
| 1) 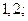 2) 2) 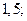 3) 3) 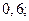 4) 4) 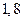
|
| А5 | Найдите значение выражения: 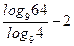
| 1) 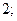 2) 2) 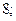 3) 3) 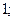 4) 4) 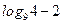
|
| А6 | Вычислите: 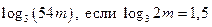
| 1) 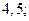 2) 2) 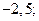 3) 3) 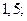 4) 4) 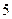
|
| А7 | Найдите значение выражения: 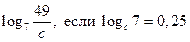
| 1) 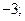 2) 2) 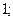 3) 3) 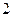 4) 4) 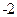
|
| А8 | Вычислите 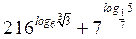
| 1) 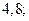 2) 2) 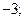 3) 3) 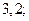 4) 4) 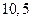
|
2.Определите множество значений функции:
| А1 | Определите множество значений функции:
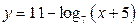
| 1) 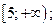 2) 2) 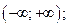 3) 3) 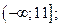 4) 4) 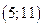
|
| А2 | Определите множество значений функции:
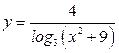
| 1) 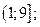 2) 2) 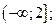 3) 3) 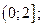 4) 4) 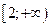
|
| А3 | Определите множество значений функции:
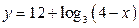
| 1) 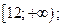 2) 2) 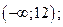 3) 3) 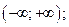 4) 4) 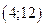
|
| А4 | Определите множество значений функции:
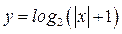
| 1) 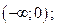 2) 2) 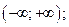 3) 3) 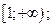 4) 4) 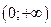
|
| А5 | Определите множество значений функции:
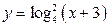
| 1) 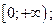 2) 2) 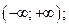 3) 3) 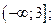 4) 4) 
|
| А6 | Определите множество значений функции:
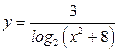
| 1) 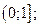 2) 2) 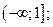 3) 3) 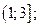 4) 4) 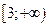
|
| А8 | Определите множество значений функции:
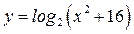
| 1) 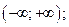 2) 2) 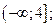 3) 3) 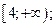 4) 4) 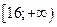
|
Практическое занятие №10
Выполнение заданий на определение параллельности прямых и плоскостей
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки по теме: «Прямые и плоскости в пространстве». Закрепить и систематизировать знания по теме.
2. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Изучить условие заданий для практической работы.
2. Ответить на контрольные вопросы.
3. Оформить отчет о работе.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1.В треугольнике АВС середины сторон АВ и ВС лежат в плоскости α, а сторона АС не лежит в этой плоскости. Докажите, сто прямая АС параллельна плоскости α.
2. Известно, что прямые a и b параллельны, прямая а перпендикулярна плоскости α, прямая с лежит в плоскости α. Каково взаимное расположение прямых b и с? Сделайте чертеж и обоснуйте ответ
3. Дан прямоугольник со сторонами 3 и 4см, в точке пересечения диагоналей прямоугольника восстановлен перпендикуляр к плоскости прямоугольника, длина которого 7см. Найти расстояние от вершины перпендикуляра до вершин прямоугольника.
4. Прямые а и с параллельны, а прямые а и b пересекаются. Могут ли прямые b и с быть параллельными? Ответ обоснуйте.
5. Точки А и В расположены по одну сторону плоскости α, АС и ВD – перпендикуляры к этой плоскости, АС=6 см, ВD=3 см, СD=18 см. Найдите расстояние между точками А и В.
Вариант 2.
1.Дан куб АВСDА1В1С1D1. Выпишите: а) две пары ребер, принадлежащих параллельным прямым; б) две пары ребер, принадлежащих скрещивающимся прямым; в) две пары граней, принадлежащих параллельным плоскостям.
2. Длина наклонной 18 см. Угол между наклонной и плоскостью 300. Чему равна длина проекции наклонной на эту плоскость?
3. Дан прямоугольный треугольник со сторонами 3 и 4см, в вершине острого угла восстановлен перпендикуляр к плоскости треугольника, длина которого 7см. Найти расстояние от вершины перпендикуляра до вершин треугольника.
1.Даны параллелограмм АВСD и точка Р, не лежащая в плоскости АВС. Как расположена прямая АС и плоскость РВD? Ответ обоснуйте
3. Из точки лежащей вне плоскости проведены к этой плоскости две наклонные под углом 300, равные. Их проекции образуют между собой угол 1200. Определить расстояние между основаниями наклонных.
Контрольные вопросы по теме
1 . Что такое стереометрия?
2. Сформулируйте аксиомы стереометрии.
3. Какие прямые в пространстве называются параллельными?
4. Какие прямые называются скрещивающимися?
5. Что значит: прямая и плоскость параллельны?
6. Признак параллельности прямой и плоскости.
7. Какие плоскости называются параллельными? Докажите призрак параллельности плоскостей.
8. Докажите, что если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
9. Докажите, что отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.
10. Перечислите случаи взаимного расположения в пространстве: а) двух прямых;
б) прямой и плоскости; в) двух плоскостей.
11. Что называется углом между: а) двумя прямыми; б) прямой и плоскостью;
12. Сформулируйте теоремы о взаимном расположении прямых и плоскостей в пространстве.
Практическое занятие №11
Решение задач на нахождение углов и расстояний в пространстве
Цель урока: отработка навыков решения задач на нахождение углов и расстояний в пространстве.
Ко всем задачам обязательно выполняем чертеж и записываем условия (дано, доказать/найти, доказательство/решение).
| Вариант 1 | Вариант 2 |
| 1. Прямая с пересекает прямую a и не пересекает прямую b, параллельную прямой а. Докажите, что b и с – скрещивающиеся прямые. | 1. Прямая m пересекает сторону AB треугольника АВС. Каково взаимное расположение прямых m и ВС, если: а) прямая m лежит в плоскости АВС и не имеет общих точек с отрезком АС; б) прямая m не лежит в плоскости АВС? |
| 2. На скрещивающихся прямых а и b отмечены соответственно точки M и N. Через прямую а и точку N проведена плоскость α, а через прямую b и точку М – плоскость β. А) Лежит ли прямая b в плоскости α? Б) Пересекаются ли плоскости α и β? При положительном ответе укажите прямую, по которой они пересекаются. | 2. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой? Ответ обоснуйте. |
3. Прямые BD и АС параллельные, а ВО и АС – скрещивающиеся прямые. Найдите угол между прямыми ВО и АС, если а) 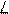 ОВD = 400
б) ОВD = 400
б) 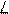 ОВD = 1350 в) ОВD = 1350 в) 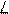 ОВD = 900 ОВD = 900
| 3. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма. Докажите, что а и CD – скрещивающиеся прямые, и найдите угол между ними, если один из углов параллелограмма равен а) 480, б) 1430 |
Практическое занятие №12
Построение сечений тетраэдра и параллелепипеда
Цель:
научить строить сечения тетраэдра и параллелепипеда плоскостью;
формировать умения анализировать, сравнивать, обобщать, делать выводы;
развивать навыки самостоятельной деятельности у обучающихся, умения работать в группе
Дата: 2018-12-21, просмотров: 452.