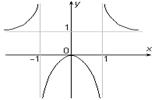
- Найти область определения функции
- Определить четность, нечетность функции
- Определить периодичность функции
- Найти промежутки монотонности функции
- Найти экстремумы функции
- Определить при необходимости дополнительные точки графика функции
- Найти область значения функции
- Построить график функции
ДОСТАТОЧНЫЙ ПРИЗНАК ВОЗРАСТАНИЯ ФУНКЦИИ
Если производная функции положительна в каждой точке некоторого промежутка, то функция возрастает на данном промежутке
ДОСТАТОЧНЫЙ ПРИЗНАК УБЫВАНИЯ ФУНКЦИИ
Если производная функции отрицательна в каждой точке некоторого промежутка, то функция убывает на данном промежутке.
ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА В ТОЧКЕ (ТОЧКА МАКСИМУМА И ТОЧКА МИНИМУМА)
Если функция непрерывна в некоторой точке и слева от неё производная функции имеет знак «+», а справа от неё производная имеет знак «-», то данная точка является точкой максимума функции на данном промежутке.
Если функция непрерывна в некоторой точке и слева от неё производная функции имеет знак «-», а справа от неё производная имеет знак «+», то данная точка является точкой минимума функции на данном промежутке.
2. Определить промежутки возрастания (убывания) точки минимума, максимума следующих функций:
2.1. 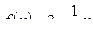
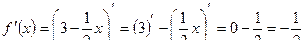
т.к. 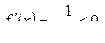 то функция убывает на всей оси ОДЗ.
то функция убывает на всей оси ОДЗ.
2.2. 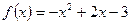

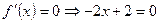
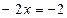
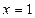 -критическая точка.
-критическая точка.

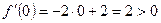
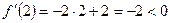
Функция возрастает на 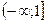
Функция убывает на 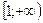
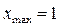
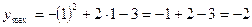
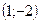 - точка максимума.
- точка максимума.
2.3. 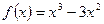
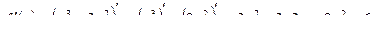
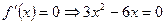

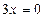 или
или 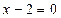
х = 0 х = 2 - критические точки
2.4. 
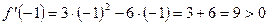
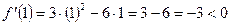
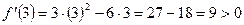
Функция возрастает на 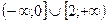
Функция убывает на 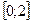
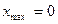
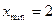

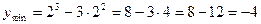
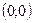 - точка максимума
- точка максимума 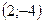 - точка минимума
- точка минимума
3. Выполнить задание с дальнейшей самопроверкой.
3.1. Исследовать функцию на промежутки монотонности и точки экстремума.
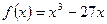
Ответ: функция возрастает на 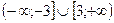
функция убывает на 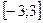
точка максимума 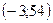
точка минимума 
3.2. Определить промежутки убывания и точки максимума функции.
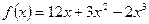
Ответ: функция убывает на 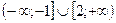
точка максимума 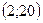
3.3. Определить промежутки возрастания и точки минимума функции.
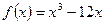
Ответ: функция возрастает на 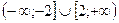
точка минимума 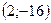
Выходной контроль.
Вариант
- Исследовать функцию на промежутки монотонности и экстремумы функции:
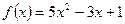
- определить промежутки возрастания функции и точку минимума:
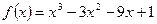
2. Вариант
- Исследовать функцию на промежутки монотонности и экстремумы функции:
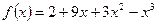
- Определить промежутки убывания и точку максимума:
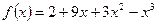
3 Вариант
- Исследовать функцию на промежутки монотонности и экстремумы функции:
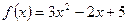
- Определить промежутки возрастания и точки минимума:
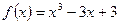
Вариант
- Исследовать функцию на промежутки монотонности и экстремумы функции:
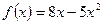
- Определить промежутки убывания и точки максимума:
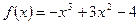
Оценка: «3» - задание 1
«4 и 5» - задание 1,2
Практическое занятие №40
Выполнение заданий на исследование и построение графиков функций
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки по теме: «Исследование функции и построение ее графика».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какую точку называют критической (стационарной) точкой функции?
б) Сформулируйте признак возрастания (убывания) функции.
в) Сформулируйте признак максимума (минимума) функции.
г) Опишите схему исследования функции.
2. С помощью обучающей таблицы повторить план исследования функции и изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля (в таблице).
4. Изучить условие заданий для практической работы.
5. Оформить отчет о работе.
ОБУЧАЮЩАЯ ТАБЛИЦА
Задание. Исследуйте и постройте графики функции:
а) 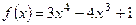 ;б)
;б) 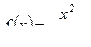 .
.
| № | План исследования | Применение | плана | ||
| шага | Функции | а) 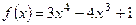
| б) 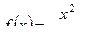
| ||
| Находим область определения функции | 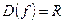
| 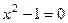 , , 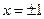 , , 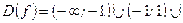 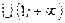
| |||
| Исследуем функцию на четность, нечетность | 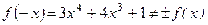 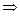 функция ни четная, ни нечетная функция ни четная, ни нечетная
| 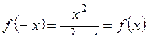 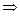 функция четная функция четная
| |||
| Находим нули (корни) функции и промежутки её знакопостоянства | 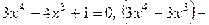 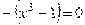 , , 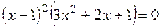 , , 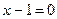 , ,  - нуль функции - нуль функции
| 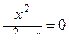 , , 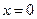 - нуль функции - нуль функции 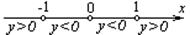
| |||
| Находим производную функции и её критические точки | 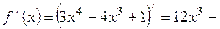 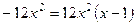 , , 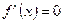 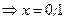 - критические точки функции - критические точки функции
| 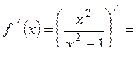 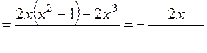 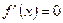 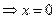 - критическая точка функции - критическая точка функции
| |||
| Находим промежутки монотонности, точки экстремума и экстремумы функции |
х=0 – не является точкой экстремума, х=1 – точка минимума, | 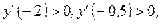 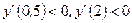 , х=0 – точка максимума, , х=0 – точка максимума, 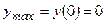
| |||
Находим предел функции при 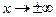
| 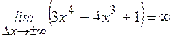
| 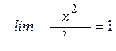
| |||
7 | Строим эскиз графика функции | 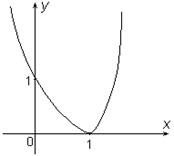
|
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Исследуйте функцию 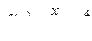 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 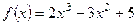 и постройте ее график.
и постройте ее график.
3. Найдите наибольшее и наименьшее значения функции 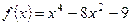 на отрезке
на отрезке 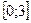 .
.
Вариант 2.
1. Исследуйте функцию 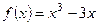 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 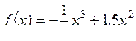 и постройте ее график.
и постройте ее график.
3. Найдите наибольшее и наименьшее значения функции 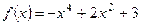 на отрезке
на отрезке 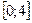
Вариант 3.
1. Исследуйте функцию 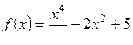 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 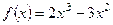 и постройте ее график.
и постройте ее график.
3. Найдите наибольшее и наименьшее значения функции 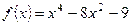 на отрезке
на отрезке 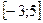
Вариант 4.
1. Исследуйте функцию 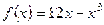 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 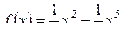 и постройте ее график.
и постройте ее график.
3. Найдите наибольшее и наименьшее значения функции 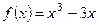 на отрезке
на отрезке 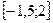
Практическое занятие № 41
Отработка навыков нахождения наибольшего и наименьшего значения функции
Цель: создание содержательных и организационных условий для самостоятельного применения учащимися комплексных знаний по нахождению наибольшего и наименьшего значений функции на отрезке с помощью производной, вырабатывать у учащихся навыки решения задач, воспитание терпения, усидчивости, самостоятельности.
Основные термины и понятия: область определения, область значения функции, наибольшее и наименьшее значения функции на отрезке, критические точки.
Планируемые результаты обучения: уч-ся должны знать алгоритм нахождения наибольшего и наименьшего значений функции на отрезке, решать задачи с помощью данного алгоритма.
Тип урока: комплексное применение знаний и способов деятельности
Форма урока: комбинированный урок
Ход урока
- Самостоятельное применение знаний
Выполнение лабораторно-практической работы
I вариант


II вариант


III вариант


Практическое занятие 42
Выполнение заданий на нахождение площадей фигур с помощью интегралов
Образовательные задачи:
· обеспечить повторение, обобщение и систематизацию материала по данной теме;
· создать условия контроля (самоконтроля) знаний и умений.
Развивающие задачи:
· способствовать формированию умений применять приемы сравнения, обобщения, выделения главного;
· продолжить развитие математического кругозора, мышления и речи, внимания и памяти.
Воспитательные задачи:
· содействовать воспитанию интереса к математике;
· воспитание активности, мобильности, умения общаться.
1. С учетом алгоритма выполните задание.

Рисунок 1
Решение:
Найдём пределы интегрирования.
Для точки А:
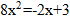
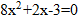
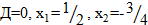
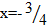 – не удовлетворяет условию задания
– не удовлетворяет условию задания
Для точки В:
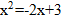
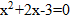
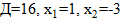
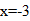 – не удовлетворяет условию задачи.
– не удовлетворяет условию задачи.
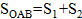
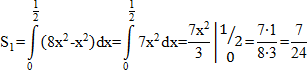
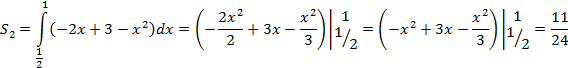
Ответ: 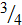 (кв. ед).
(кв. ед).
2. Но при выполнении этого задания алгоритм применялся не полностью. Для его отработки выполним следующее задание
Задание. Найти площадь фигуры, ограниченной линиями 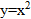 ,
, 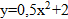 .
.
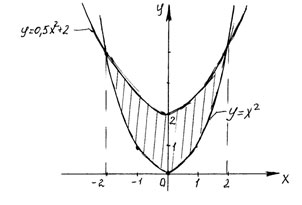
Рисунок 2
Решение:
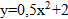 – парабола, вершина (m,n).
– парабола, вершина (m,n).
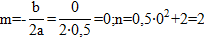
(0;2) – вершина
| -2 | 0 | 2 |
| 4 | 2 | 4 |
Найдём пределы интегрирования.
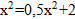
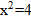
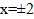
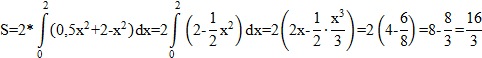
Ответ: 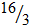 (кв.ед).
(кв.ед).
Вычислите определённые интегралы и вы узнаете одно из высказываний французского математика С.Д.Пуассона.
| 1 | 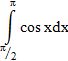
|
| 2 | 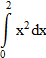
|
| 3 | 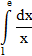
|
| 4 | 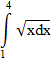
|
| 5 | 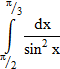
|
| 6 | 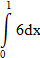
|
| 7 | 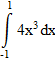
|
| 8 | 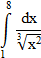
|
| 9 | 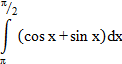
|
| Жизнь | -1 | Тремя | -16 |
| Двумя | 1 | Вещами | 7 |
| Занятием | 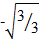
| И | 0 |
| Математикой | 6 | Арифметикой | 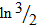
|
| Преподаванием | 0 | Её | 3 |
| Украшается | 
| Забыванием | 0 |
Используя определенный интеграл, запишите формулы для вычисления площадей фигур, заштрихованных на рисунке.
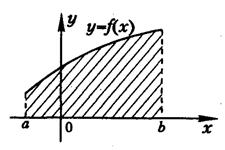 _________________________________________
_________________________________________
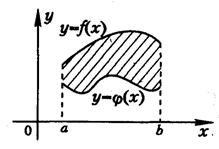 __________________________________________
__________________________________________
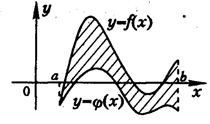 ___________________________________________
___________________________________________
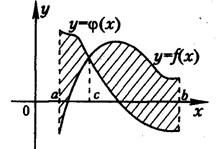 ___________________________________________
___________________________________________
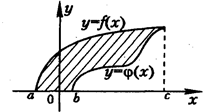 ____________________________________________
____________________________________________
Дата: 2018-12-21, просмотров: 456.