1. Записать координаты вектора 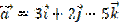
2. Даны векторы 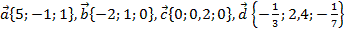 .
.
Найти координаты векторов: а) 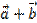 , б)
, б) 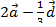
3. Даны координаты точек A,B,C,D. Равны ли векторы 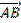 и
и 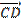 ?
?
A(3;-1;5), B(8;-4;8), C(3;-1;0), D(8;0;3).
4. Найти координаты середины отрезка ВС. Координаты точек В и С взять из задания 3.
5. Найти скалярное произведение векторов 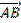 и
и 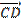 . Координаты точек A,B,C,D взять из задания 3.
. Координаты точек A,B,C,D взять из задания 3.
6. Даны векторы 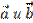 . Определите, какой угол (острый, прямой или тупой) между ними.
. Определите, какой угол (острый, прямой или тупой) между ними.
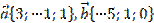
7. Точка М – середина отрезка АВ. Найти координаты точки: а) М, если A(0;3;-4), B(-2;2;0)
б) В, если A(14;-8;5), М(3;-2;-7).
8. Даны координаты вершин треугольника A(9;3;-5), B(2;10;-5), C(2;3;2). Найти периметр этого треугольника и косинусы его углов.
Вариант 2
Действия над векторами, заданными координатами
1. Записать координаты вектора 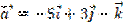
2. Даны векторы 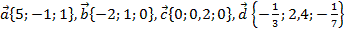 .
.
Найти координаты векторов: а) 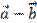 , б)
, б) 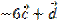
3. Даны координаты точек A,B,C,D. Равны ли векторы 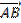 и
и 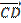 ?
?
A(-1;0;2), B(-5;4;1), C(-3;4;5), D(-7;8;4).
4. Найти координаты середины отрезка ВС. Координаты точек В и С взять из задания 3.
5. Найти скалярное произведение векторов 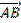 и
и 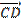 . Координаты точек A,B,C,D взять из задания 3.
. Координаты точек A,B,C,D взять из задания 3.
6. Даны векторы 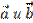 . Определите, какой угол (острый, прямой или тупой) между ними.
. Определите, какой угол (острый, прямой или тупой) между ними.
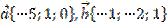
7. Точка М – середина отрезка АВ. Найти координаты точки: а) М, если A(0;6;-8), B(-2;2;0)
б) В, если A(7;-4;2,5), М(3;-2;-7).
8. Даны координаты вершин треугольника A(3;7;-4), B(5;-3;2), C(1;3;-10). Найти периметр этого треугольника и косинусы его углов.
Вариант 3
Действия над векторами, заданными координатами
1. Записать координаты вектора 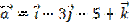
2. Даны векторы 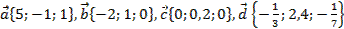 .
.
Найти координаты векторов: а) 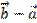 , б)
, б) 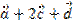
3. Даны координаты точек A,B,C,D. Равны ли векторы 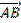 и
и 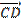 ?
?
A(0;3;-4), B(4;-8;3), C(7;0;-1), D(3;10;-6).
4. Найти координаты середины отрезка ВС. Координаты точек В и С взять из задания 3.
5. Найти скалярное произведение векторов 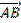 и
и 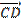 . Координаты точек A,B,C,D взять из задания 3.
. Координаты точек A,B,C,D взять из задания 3.
6. Даны векторы 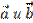 . Определите, какой угол (острый, прямой или тупой) между ними.
. Определите, какой угол (острый, прямой или тупой) между ними.
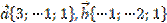
7. Точка М – середина отрезка АВ. Найти координаты точки: а) М, если A(0;3;-4), B(-4;4;0)
б) В, если A(14;-8;5), М(6;-4;-14).
8. Даны координаты вершин треугольника A(5;-5;-1), B(5;-3;-1), C(4;-3;0). Найти периметр этого треугольника и косинусы его углов.
Вариант 4
Действия над векторами, заданными координатами
1. Записать координаты вектора 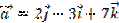
2. Даны векторы 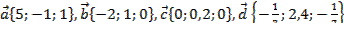 .
.
Найти координаты векторов: а) 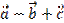 , б)
, б) 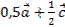
3. Даны координаты точек A,B,C,D. Равны ли векторы 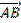 и
и 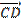 ?
?
A(9;3;-5), B(-3;-1;7), C(-1;-1;-4), D(-11;-3;-8).
4. Найти координаты середины отрезка ВС. Координаты точек В и С взять из задания 3.
5. Найти скалярное произведение векторов 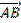 и
и 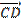 . Координаты точек A,B,C,D взять из задания 3.
. Координаты точек A,B,C,D взять из задания 3.
6. Даны векторы 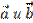 . Определите, какой угол (острый, прямой или тупой) между ними.
. Определите, какой угол (острый, прямой или тупой) между ними.
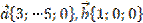
7. Точка М – середина отрезка АВ. Найти координаты точки: а) М, если A(0;9;-12), B(-2;2;0)
б) В, если A(14;-8;5), М(-6;4;14).
8. Даны координаты вершин треугольника A(-5;2;0), B(-4;3;0), C(-5;2;-2). Найти периметр этого треугольника и косинусы его углов.
Практическое занятие №20
Определение синуса, косинуса и тангенса
Цель занятия:
- овладение умениями изображать графики тригонометрических функций и описывать их свойства;
2. Дидактическое оснащение практического занятия: методические указания по выполнению практического занятия; инструменты: линейка, карандаш, ластик.
Пояснение к работе
3.1 Краткие теоретические сведения
Определение 1. Если точка М числовой окружности соответствует числу t , то абсциссу точки М называют косинусом числа t и обозначают cos t, а ординату точки М называют синусом числа t и обзначают sin t.
Итак, если М(t) = М (х;у) , то х = cos t, у = sin t.
Определение 2. Отношение синуса числа t к косинусу числа t называют тангенсом числа t и обозначают tg t.
Определение 3.
Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают сtg t .
Функции, заданные формулами:
У = sinх, у = cos х, у = tg х, у = сtg х называют тригонометрическими.
Образец решения
Пример 1. График и свойства функции у = sinх
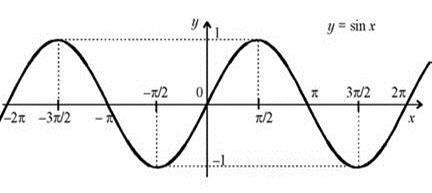
Рис. 1
Описание свойств функции у = sinх
Таблица 1 Свойства функции у = sinх
| 1. Область определения | R |
| 2. Область значений | [-1; 1] |
| 3. Четность (нечетность) | нечетная |
| 4. Наименьший положительный период | 2π |
| 5. Координаты точек пересечения графика f с осью Ох | (πn; 0) |
| 6. Координаты точек пересечения графика f с осью Оу | (0;0) |
| 7. Промежутки, на которых функция принимает положительные значения | (2πn; π+2πn) |
| 8. Промежутки, на которых функция принимает отрицательные значения | ( - π+2πn; 2πn) |
| 9. Промежутки возрастания | [ - π/2 +2πn; π/2 +2πn ] |
| 10. Промежутки убывания | [ π/2 +2πn; 3π/2 +2πn ] |
| 11. Точки минимума | - π/2 +2πn |
| 12. Минимумы функции | -1 |
| 13. Точки максимума | π/2 +2πn |
| 14. Максимумы функции | 1 |
Задание
Постройте в тетради графики тригонометрических функций, учитывая масштаб: единичный отрезок по оси абсцисс – 3 клетки тетради, по оси ординат – 2 клетки тетради опишите их свойства по образцу примера 1
А) y = cos x
Б) y =tg x
В) y = ctg x
6. Контрольные вопросы
Рис. 2
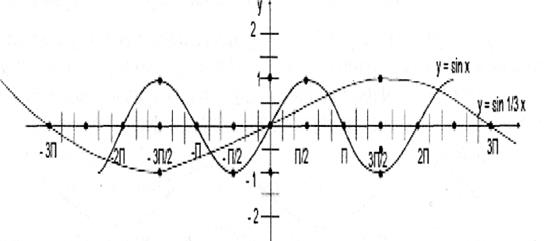
А)Чему равен период функции у = sin 1/3x, изображенной на рис.2?
Б) В каких точках функция принимает максимальное и минимальное значения?
Практическое занятие №21
Тригонометрические тождества
Цель: Научиться преобразовывать тригонометрические выражения с использованием основных тригонометрических тождеств.
Оснащение рабочего места: инструкционная карта, микрокалькулятор.
СОДЕРЖАНИЕ РАБОТЫ.
Задание 1.1.Дано:  ,
, 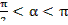 . Вычислить: 1)
. Вычислить: 1) 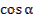 2)
2) 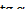 3)
3) 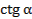
2. Дано: 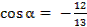 ,
, 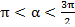 . Вычислить: 1)
. Вычислить: 1) 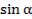 2) )
2) ) 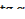 3)
3) 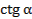
3. Дано: 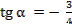 ,
, 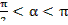 . Вычислить: 1)
. Вычислить: 1) 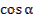 2)
2) 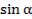 3)
3) 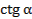
4. Дано: 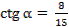 ,
, 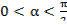 . Вычислить: 1)
. Вычислить: 1) 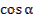 2)
2) 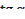 3)
3) 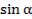
Задание 2.Упростить выражения
1. 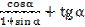
2. sin4 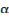 + cos4
+ cos4 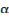 +2sin2
+2sin2 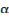 cos2
cos2 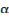
Методические указания
Для решения практической работы используются
«Основные тригонометрические тождества»
sin2 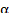 +cos2 +cos2 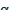 =1 =1
| 1+ tg2 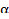 = = 
|
tg 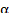 ctg ctg  =1 =1
| 1+ ctg2 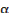 = = 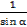
|
и таблица нахождения функции через данную тригонометрическую функцию.
Контрольные вопросы
1. Какие функции называют тождественно равными?
2. Какие приемы используются при доказательстве тригонометрических функций?
3. Что называется тождеством?
Практическое занятие № 22
Применение тригонометрических тождеств к преобразованию тригонометрических выражений
Цель: учащиеся должны научиться преобразовывать тригонометрические выражения.
Задачи:
1. Формирование навыков применения основных тригонометрических тождеств для преобразования выражений, доказательства тождеств.
2. Развитие логического мышления при преобразовании выражений.
Тригонометрический тренажер.
Вычислите: 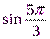 ;
; 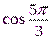 ;
; 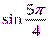 ;
; 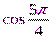 ;
; 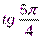 ;
; 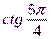 .
.
Вычислите: а) 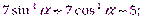
б) 
Значения тригонометрических функций.
№1. Упростить выражение:
cos2 α + 1 + sin2 α
№2. Дробь 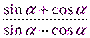 выразить через tg α и вычислить, если tg α=5.
выразить через tg α и вычислить, если tg α=5.
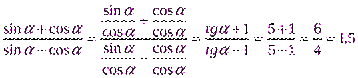
№3. Доказать тождество: 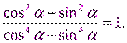
№4. Доказать тождество: 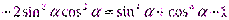 .
.
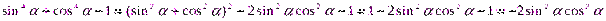
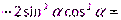
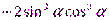
№5. Доказать тождество: 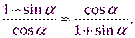
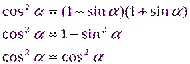
Работа на доске и в тетрадях.
1. Найдите значение выражения 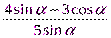 , если tg α=2.
, если tg α=2.
2. Приведите к более простому виду выражение: 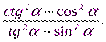
3. Докажите тождество: 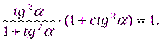
4. Упростить выражение: 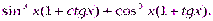
Практическое занятие № 23
Выполнение заданий с применением формул сложения
Формулы сложения.
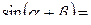
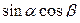 +
+ 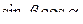
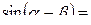
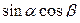 -
- 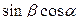
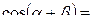
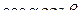 -
- 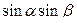
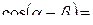
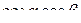 +
+ 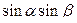
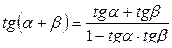
№ 1. С помощью формул сложения вычислить:
1) 
2) 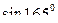
3) 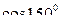
4) 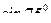
5) 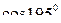
6) 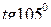
№ 2. Вычислить:
1) 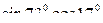 +
+ 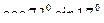
2) 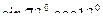 -
- 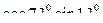
3) 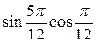 +
+ 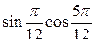
4) 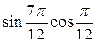 -
- 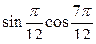
5) 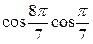 +
+ 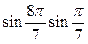
6) 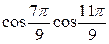 -
- 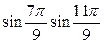
7) 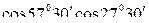 +
+ 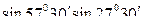
8) 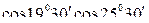 -
- 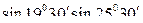
№ 3. Вычислить:
1) 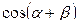 , если
, если 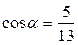 ,
, 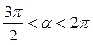 ,
, 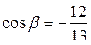 ,
, 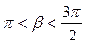
2) 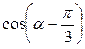 , если
, если 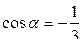 ,
, 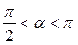
3) 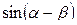 , если
, если 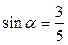 ,
, 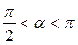 ,
, 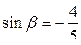 ,
, 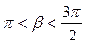
4) 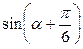 , если
, если 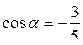 ,
, 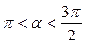
№4. Упростить выражения:
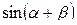 +
+ 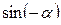
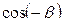
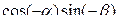 -
- 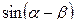
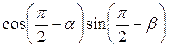 -
- 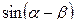
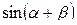 +
+ 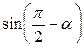
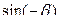
Тригонометрические функции двойного аргумента.
Выведем формулы, синуса и косинуса двойного угла, используя формулы сложения.
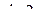 =
= 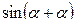 =
= 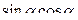 +
+  =
= 
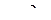 =
= 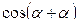 =
= 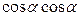 -
- 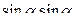 =
= 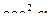 -
- 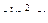
Пример 1. Вычислить 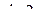 , если
, если 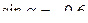 ,
, 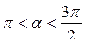
Решение: 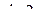 =
=  =
= 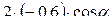 =
= 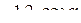
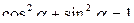
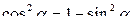
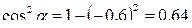
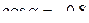 т.к.
т.к. 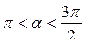
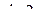 =
= 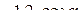 =
= 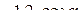 =
= 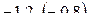 = 0,96
= 0,96
Пример 2. Вычислить  , если
, если 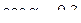
Решение: 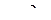 =
= 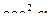 -
- 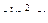 =
= 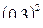 -
- 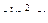 = 0,09 -
= 0,09 - 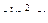
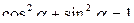
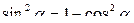
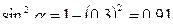
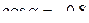 т.к.
т.к. 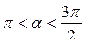
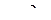 = 0,09 -
= 0,09 - 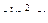 = 0,09 – 0,91 = - 0,82
= 0,09 – 0,91 = - 0,82
№ 1. Выразить синус, косинус, используя формулы двойного аргумента
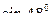
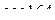
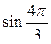
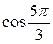
№2. Вычислить:
1) 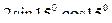
2) 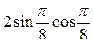
№3. Вычислить:
3) 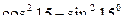
4) 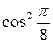 -
- 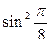
5) 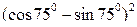
1) 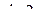 , если
, если 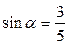 ,
, 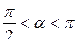
2) 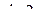 , если
, если 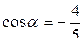 ,
, 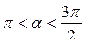
3) 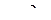 , если
, если 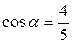
4) 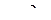 , если
, если 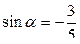
Практическое занятие № 24
Выполнение заданий с применением формул двойных углов
Цель:
- вывести формулы двойного угла;
- учить применять формулы для упрощения тригонометрических выражений;
№ 1
Вычислите:
а) 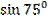 =
= 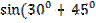 ) =
) = 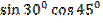 +
+ 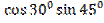 =
=
= 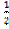
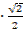 +
+ 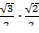 =
= 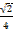 +
+ 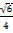 .
.
б) 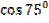 =
= 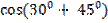 =
= 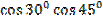 +
+ 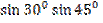 =
=
= 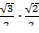 -
- 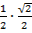 =
= 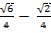 .
.
№ 2
Докажите тождество:
а) 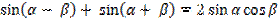 .
.
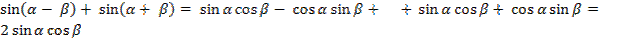 .
.
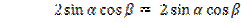 .
.
 .
.
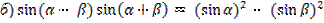 .
.
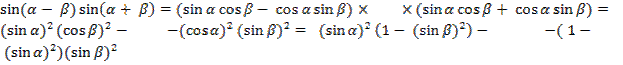 =
= 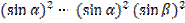 - –
- – 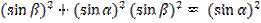 –
– 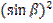 .
.
 –
– 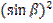 =
= 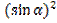 –
– 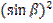 .
.
 .
.
№ 3
Косинусы двух острых углов треугольника равны  и
и  . Найдите синус третьего угла.
. Найдите синус третьего угла.
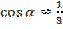 ;
; 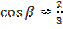 . Найти
. Найти 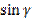 .
.
Т. к. 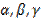 углы треугольника, то это углы I или II четверти.
углы треугольника, то это углы I или II четверти.
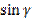 =
= 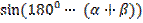 =
= 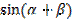 =
= 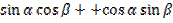 .
.
1) 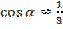
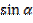 =
= 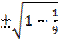 =
= 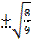 =
= 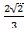 ,т.к.
,т.к. 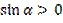 .
.
2) 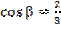
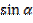 =
= 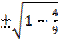 =
= 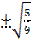 =
= 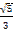 ,т.к.
,т.к. 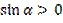 .
.
3) 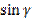 =
= 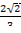
 +
+ 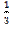
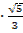 =
= 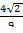 +
+ 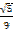 .
.
Ответ: 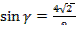 +
+ 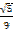 .
.
«Формулы двойного угла»
№ 1
Запишите угол в виде 2 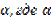 - некоторый угол:
- некоторый угол:
а) 300; б) 900; в) 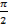 ; г)
; г) 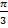 ; д) 4
; д) 4 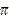 ; е)
; е) 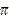 ; ж)
; ж) 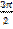 .
.
№ 2
Упростите выражение:
а) 2 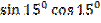
б) 4 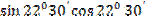
в) 5 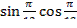
г) 4 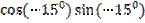
№ 3
Упростите выражение:
а) 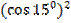 –
– 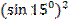
б) 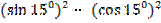
в) 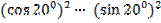
г) ( 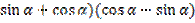
№ 4
Упростите выражение:
а) 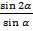 ; б)
; б) 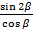 ; в)
; в) 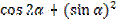 ; г)
; г) 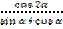 -
- 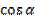 .
.
Самостоятельная работа
Упростите выражение:
Вариант 1.
1) 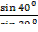 ; 2)
; 2) 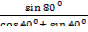 .
.
Вариант 2.
1) 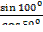 ; 2)
; 2) 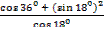 .
.
Ответы.
Вариант 1: 1) 2 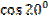 ; 2)
; 2) 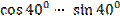 .
.
Вариант 2: 1) 2 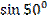 ; 2)
; 2) 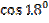 .
.
Дата: 2018-12-21, просмотров: 2710.