

Логарифм произведения — это сумма логарифмов
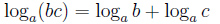
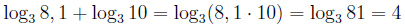
Логарифм частного — это разность логарифмов
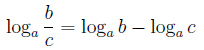
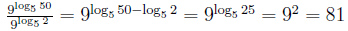
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа 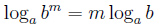
Показатель степени основания логарифма 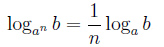
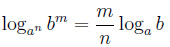 ,
,
в частности если m = n, мы получаем формулу: 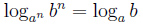 ,
,
например: 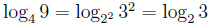
Переход к новому основанию
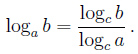 , частности, если c = b, то
, частности, если c = b, то 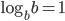 , и тогда:
, и тогда:
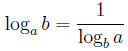

Логарифмирование – это нахождение логарифмов заданных чисел или выражений.
b
Пример: Найдем логарифм x = a2 · — .
c
Решение.
Последовательно воспользуемся сразу всеми тремя основными свойствами логарифмов, которые изложены выше (логарифм произведения, логарифм частного и логарифм степени):
b
lg x = lg (a2 · —) = lg a2 + lg b – lg c = 2lg a + lg b – lg c.
c
Потенцирование – это нахождение чисел или выражений по данному логарифму числа (выражения).
Потенцировать – значит освобождаться от значков логарифмов в процессе решения логарифмического выражения.
Например, надо решить уравнение log2 3x = log2 9.
Убираем значки логарифмов – то есть потенцируем:
3х = 9.В результате получаем простое уравнение, которое решается за несколько секунд:
х = 9 : 3 = 3.
Но потенцирование не сводится к простому и произвольному убиранию значков логарифмов. Для этого в обоих частях уравнения как минимум должно быть одинаковое значение основания (в нашем случае это число 2).
Вариант – 1
1. Вычислить:
а) 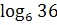 ;
б) ;
б) 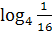 ;
в) ;
в) 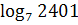 ;
г) ;
г) 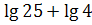 .
д) .
д) 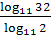 2. Найдите x, если
2. Найдите x, если 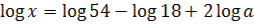 .
3. Известно, что .
3. Известно, что  , найдите , найдите 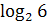 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
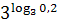 , , 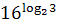 , , 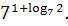 5. Прологарифмируйте по основанию 3 (a>0, b>0)
5. Прологарифмируйте по основанию 3 (a>0, b>0)
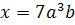 . .
| Вариант – 2
1. Вычислить:
а) 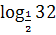 ;
б) ;
б) 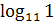 ;
в) ;
в) 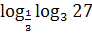 ;
г) ;
г) 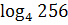 .
д) .
д) 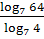 2. Найдите x, если
2. Найдите x, если 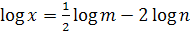 .
3. Известно, что .
3. Известно, что 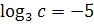 , найдите , найдите 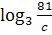 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
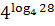 , , 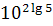 , , 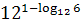 .
5. Прологарифмируйте по основанию 2 (a>0, m>0) .
5. Прологарифмируйте по основанию 2 (a>0, m>0)
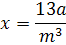
|
Вариант – 3
1. Вычислить:
а) 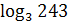 ;
б) ;
б) 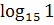 ;
в) ;
в) 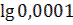 ;
г) ;
г) 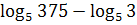 .
д) .
д) 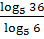 2. Найдите x, если
2. Найдите x, если 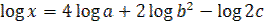 .
3. Известно, что .
3. Известно, что 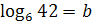 , найдите , найдите 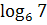 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
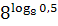 , , 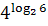 , , 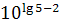 .
5. Прологарифмируйте по основанию 10 (a>0, b>0) .
5. Прологарифмируйте по основанию 10 (a>0, b>0)
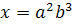 . .
| Вариант – 4
1. Вычислить:
а) 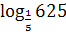 ;
б) ;
б) 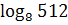 ;
в) ;
в) 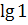 ;
г) ;
г) 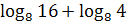 .
д) .
д) 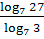 2. Найдите x, если
2. Найдите x, если 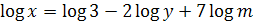 .
3. Известно, что .
3. Известно, что 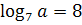 , найдите , найдите 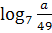 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
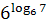 , , 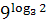 , , 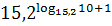 .
5. Прологарифмируйте по основанию 4 (c>0, b>0) .
5. Прологарифмируйте по основанию 4 (c>0, b>0)
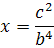
|
Вариант – 5
1. Вычислить:
а) 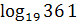 ;
б) ;
б) 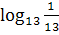 ;
в) ;
в) 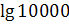 ;
г) ;
г) 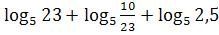 .
д) .
д) 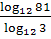 2. Найдите x, если
2. Найдите x, если 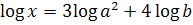 .
3. Известно, что .
3. Известно, что 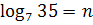 , найдите , найдите 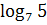 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
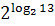 , , 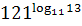 , , 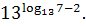 5. Прологарифмируйте по основанию 10 (a>0, c>0)
5. Прологарифмируйте по основанию 10 (a>0, c>0)
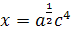 . .
| Вариант – 6
1. Вычислить:
а) 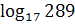 ;
б) ;
б) 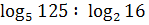 ;
в) ;
в) 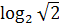 ;
г) ;
г) 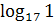 ;
д) ;
д) 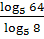 2. Найдите x, если
2. Найдите x, если
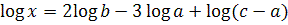 .
3. Известно, что .
3. Известно, что 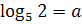 , найдите , найдите 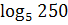 .
4. Упростите выражение, пользуясь основным логарифмическим тождеством .
4. Упростите выражение, пользуясь основным логарифмическим тождеством
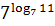 , , 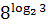 , , 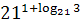 .
5. Прологарифмируйте по основанию 2 (a>0, b>0, c>0) .
5. Прологарифмируйте по основанию 2 (a>0, b>0, c>0)
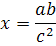
|
Практическое занятие № 9
Действия с логарифмическими выражениями
Цель работы: закрепить знания и умения студентов по освоению логарифмов и свойств логарифмической функции.
Теоретическое обоснование:
1. Основные свойства логарифмов
Дата: 2018-12-21, просмотров: 395.